Aerodynamic Propeller

Propeller that generates thrust from rotational motion

Since R2022b

Libraries:
Simscape / Driveline / Engines & Motors

Description

The Aerodynamic Propeller block represents a propeller that converts a rotational mechanical motion into thrust for aerodynamic applications. You can parameterize the propeller by using constants, polynomials, or tabulated data to characterize the thrust and power or coefficients. You can provide tabulated advance velocity data, tabulated advance angle data, or tabulated airfoil lift and drag coefficient data. When you model inertia, the default block parameters represent a 10 kg, two-blade propeller with a 1.5 m diameter.

You can use a physical signal to control the blade pitch.

This terminology is helpful for understanding the block:

Advance velocity is the speed of the flow through the propeller, V_a.
Advance ratio is the speed of the flow through the propeller with respect to the propeller tip angular speed expressed as a ratio. The block uses this to determine k_T and k_P when you set Parameterization to Polynomial fit or Tabulated data for advance ratio.
Advance angle is the angular location of the propeller operational conditions on a four quadrant plot. The block uses this to determine C_T and C_Q when you set Parameterization to Tabulated data for advance ratio.
Quadrant is the relative two-dimensional location of the propeller operating condition where the vertical axis is V_a and the horizontal axis is ω.
Pitch angle is the angle between the plane of the blade rotation and the chord line of the blade.

The block equations refer to these quantities:

T is the propeller thrust.
Q is the propeller torque.
ρ is the fluid density. You can specify the fluid density using the Density parameter or the Rho port.
θ is the pitch angle.
D is the Propeller diameter parameter.
ω is the propeller angular speed input at port R. For more information about using angular units in Simscape™, see Angular Units.
n is the propeller angular speed in revolutions per second, which consistently nondimensionalizes the power and thrust. The block defines ω = 2πn.
n_Thr is the Rotational speed threshold parameter.
ε is the Propeller direction parameter.
k_T is the thrust coefficient with respect to the propeller rotational speed.
k_P is the power coefficient with respect to the propeller rotational speed.
p_kT is the polynomial thrust coefficient vector or 2-D matrix.
p_kP is the polynomial power coefficient vector or 2-D matrix.
C_T is the thrust coefficient with respect to the relative advance velocity.
C_Q is the torque coefficient with respect to the relative advance velocity.
k_Thr is the Saturation threshold for nondimensional coefficients parameter.
J is the advance ratio.
V_a is the advance velocity. Specify the advance velocity using the Va port.
V_R is the relative advance velocity at a blade section at 70% of the blade radius.
η is the efficiency.
C^*_T is the thrust coefficient based on the blade relative advance velocity at 70% blade radius.
C^*_T,TLU is the reference thrust coefficient vector or 2-D matrix.
C^*_Q is the torque coefficient based on the blade relative advance velocity at 70% blade radius.
C^*_Q,TLU is the reference torque coefficient vector or 2-D matrix.
β is the advance angle.
β_TLU is the reference advance angle.

Parameterizations

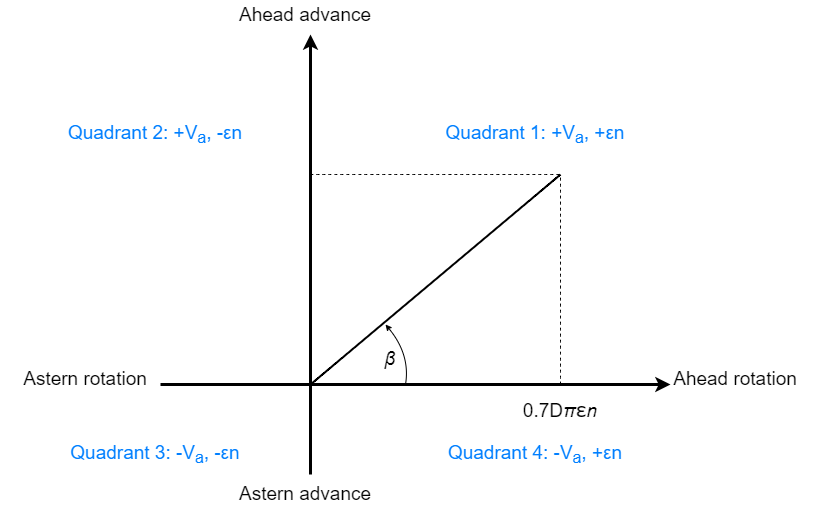
The propeller performance depends on the thrust and power coefficients. The Parameterization parameter gives you different options to control these coefficients. The propeller output depends on the quadrant where the propeller operates. The block defines the four quadrants as:

First quadrant: +V_a, +n
Second quadrant: +V_a, -n
Third quadrant: -V_a, -n
Fourth quadrant: -V_a, +n

The figure shows a visual representation of the quadrants.

Four-quadrant diagram, where ahead velocity is the positive y-axis, and ahead rotation is the positive x-axis.

When you set Parameterization to Constant coefficients, you specify the thrust and power coefficients directly. Otherwise, the block computes these coefficients depending on the Parameterization setting.

Advance Ratio

When you set Parameterization to Polynomial fit or Tabulated data for advance ratio, the block uses the advance ratio, J. The block uses a numerically smoothed version of the fundamental thrust and power equations such that

$\begin{array}{l} T = k_{T} ρ D^{4} ε n \sqrt{n^{2} + n_{t h r}^{2}} \\ Q = \frac{k_{P} ρ D^{5}}{2 π} n \sqrt{n^{2} + n_{t h r}^{2}} \end{array}$

The block defines the advance ratio as

$J = \frac{V_{a} ε n}{D (n^{2} + n_{T h r}^{2})},$

where the angular speed threshold n_Thr linearizes the propeller rotational speed, n, for smoothing.

When you set Parameterization to:

Polynomial fit — k_T and k_P vary with time according to the values you specify for the polynomial coefficient parameters. The block saturates J to be between 0 and the first positive root of the polynomial and restricts k_T and k_P to always be positive. The block calculates the thrust and power coefficients as

$\begin{array}{l} k_{T} = \sum_{j = 1 : N}^{N} p_{k T, j} J^{j} \\ k_{P} = \sum_{j = 1 : N}^{N} p_{k P, j} J^{j} \end{array}$
where p_kT and p_kP represent the polynomial coefficients.
Tabulated data for advance ratio — You specify tabulated values for k_T and k_P for given values of J or J and θ, depending on the Blade pitch type parameter.

When Efficiency sensor is on, the block calculates the efficiency as

$η = \frac{P o w e r_{o u t}}{P o w e r_{i n}} = \frac{T V_{A}}{2 π n Q} = \sqrt{J^{2} + k_{T h r}^{2}} \frac{k_{T}}{\sqrt{k_{P}^{2} + k_{T h r}^{2}}}$

Advance Angle

When you set Parameterization to Tabulated data for advance angle, the block uses thrust and power coefficients with respect to relative advance angle. The block defines the advance angle as

$β = \arctan (\frac{V_{a}}{0.7 π ε n D}),$

where β is cyclic. You must ensure that the coefficient extrapolation and cycle wrapping occur as expected. The block defines the thrust and power coefficients for relative advance velocity as

$\begin{array}{l} C_{T}^{*} = \frac{T}{\frac{1}{8} ρ V_{R}^{2} π D^{2}} \\ C_{Q}^{*} = \frac{Q}{\frac{1}{8} ρ V_{R}^{2} π D^{3}} \end{array}$

where V_R is the relative advance velocity at a blade section at 70% of the blade radius, such that

$V_{R}^{2} = V_{A}^{2} + {(0.7 D π ε n)}^{2} .$

Rearranging the coefficient equations yields the block equations for thrust and torque with respect to relative advance velocity:

$\begin{array}{l} T = C_{T}^{*} \frac{1}{8} ρ V_{R}^{2} D^{2} \\ Q = C_{Q}^{*} \frac{1}{8} ρ V_{R}^{2} D^{3} \end{array}$

When you set Blade pitch to:

Constant, the block calculates the thrust and power coefficients as

$\begin{array}{l} C_{T}^{*} = t a b l e l o o k u p (β_{T L U}, C_{T, T L U}^{*}, β, interpolation = i n t e r p_m e t h o d, extrapolation = e x t r a p_m e t h o d) \\ C_{Q}^{*} = t a b l e l o o k u p (β_{T L U}, C_{Q, T L U}^{*}, β, interpolation = i n t e r p_m e t h o d, extrapolation = e x t r a p_m e t h o d) \end{array}$
Controlled, the block calculates the thrust and power coefficients as

$\begin{array}{l} C_{T}^{*} = t a b l e l o o k u p (P / D_{T L U}, β_{T L U}, C_{T, T L U}^{*}, P / D, β, interpolation = i n t e r p_m e t h o d, extrapolation = e x t r a p_m e t h o d) \\ C_{Q}^{*} = t a b l e l o o k u p (P / D_{T L U}, β_{T L U}, C_{Q, T L U}^{*}, P / D, β, interpolation = i n t e r p_m e t h o d, extrapolation = e x t r a p_m e t h o d) \end{array}$

The basis of the propeller efficiency is the fundamental relationship

$η = \frac{P o w e r_{o u t}}{P o w e r_{i n}} = \frac{T V_{A}}{2 π ε n Q} = \frac{V_{A} C_{T}^{*}}{2 π ε n D C_{Q}^{*}} .$

When Efficiency sensor is on, the block calculates the smoothed efficiency as

$η = \frac{1}{2 π D} \sqrt{\frac{V_{A}^{2} C^{* 2} + {(D π n_{T h r} K_{T h r})}^{2}}{n^{2} C_{Q}^{* 2} + {(0.1 n_{T h r} K_{T h r})}^{2}}} .$

Blade Element Lift and Drag Coefficients

When you set Parameterization to Tabulated data for airfoil lift and drag coefficients, you can parameterize the lift and drag coefficients and the airfoil geometry for a given blade element. The block treats the propeller as a continuous disc. Conservation of momentum applies to the air that crosses the disc when the block calculates the induced velocity, v_i. The block uses the induced velocity to find the magnitude and direction of the total flow velocity at a vector of radial locations along the blade, which it then uses to find lift and drag based on the lift and drag coefficient lookup tables. These quantities are specific to this parameterization:

T_MT — Thrust calculated by momentum theory
v_i — Flow velocity induced by the motion of the propeller
v_inflow — Freestream inflow velocity of the air that the propeller experiences
v_ax — Axial velocity at the blade location
v_h — Theoretical hover-induced velocity
λ — Non-dimensionalized v_ax
g(λ) — Function the block uses for inflow
T_BET — Thrust as calculated by blade element theory
Q_BET — Torque as calculated by blade element theory
N_blades — Number of propeller blades
r — Discrete blade element location as defined by the Nondimensional radial location vector, r parameter, which the block interpolates to find y
c — Chord length for at a position along the blade, where the length is non-dimensionalized such that c = Geometric chord length/D
e — Nondimensional location of the root cutout as given by the first element of the Nondimensional radial location vector, r parameter
v_r(y) — Tangential velocity as a function of y
C_l,C_d — Element-wise coefficients of the lift and drag, respectively
ϕ(y) — Inflow angle at a given point along the blade

The block uses momentum theory to define a smoothed thrust equation such that

$T_{M T} = \frac{2 ρ π D^{2}}{4} v_{i n f l o w} \cdot v_{i},$

where the block implicitly solves for T_MT and v_i. The figure shows how the block considers translational motion. The larger area enclosed in the dotted line includes internal mass. The smaller area does not.

This figure shows how the block considers rotational motion. The larger area enclosed in the dotted line includes internal inertia. The smaller area does not.

The block smoothes v_ax to find v_inflow, which allows for transitions between forward and astern flow such that

$\begin{array}{l} v_{i n f l o w} = \sqrt{v_{a x}^{2} + v_{h}^{2} \cdot g(λ)} \\ v_{h} = \sqrt{\frac{2 \cdot | T_{M T} |}{ρ π D^{2}}} \\ λ = 2 v_{a x} / ω D \\ g (λ) = {\begin{matrix} (2 + λ) - 2 - λ^{2} + (1 + λ) \cdot (0 .109+0 .217(λ - 0.15)^{2}) & for - 1 \leq λ \leq 0.6378 \\ 0 & else . \end{matrix} \end{array}$

The block interpolates the values from the Nondimensional radial location vector, r parameter to find y. Then the block interpolates the lift and drag coefficients to find C_l(y) and C_d(y) based upon the tabulated angle of attack and lift and drag coefficients. The block uses blade element theory to calculate the thrust and torque such that

$\begin{array}{l} T_{B E T} = \frac{N_{b l a d e s} ρ D^{2}}{4} \int_{e}^{1} (v_{r}^{2} + v_{a x}^{2}) \cdot (C_{l} \cos ϕ (y) - C_{d} \sin ϕ (y)) \cdot c dy \\ Q_{B E T} = \frac{N_{b l a d e s} ρ D^{3}}{8} \int_{e}^{1} (v_{r}^{2} + v_{a x}^{2}) \cdot (C_{l} \sin ϕ (y) - C_{d} \cos ϕ (y)) \cdot c y dy \end{array}$

The block performs this integration across the each discrete blade element. The block discretizes y according to the specification in the Number of blade elements parameter. This figure summarizes the directions of forces and torques with respect to the ground.

Controlled Pitch

When you set Blade pitch type to Controlled, you can parameterize the propeller over a range of pitch angles, θ. You must specify θ as a vector in the Pitch angle vector, θ parameter, where each element corresponds to a row in both the k_T and k_P arrays.

Inertia

You can optionally include translational and rotational propeller inertia. To simulate inertia, set Rotational connections or Translational connections to Conserving, and select Model inertia. When you select Model inertia and set Rotational connections to Conserving, set the initial rotational velocity or torque on the shaft in the Initial Targets section, or set an algebraically linked variable to high priority to initialize the rotational inertia. When you select Model inertia and set Translational connections to Conserving, set the initial translational velocity or thrust in the Initial Targets section, or set an algebraically linked variable to high priority to initialize the translational mass.

Note

For rotational conserving connections, the block logs Q, the aerodynamic torque, and Inertia.t.

For translational conserving connections, the block logs thrust, the aerodynamic thrust, and mass.f.

You can use an Ideal Torque Sensor or Ideal Force Sensor blocks to log the sum of the inertia and the aerodynamic torque or force, respectively.

Assumptions and Limitations

The block treats the fluid velocity as quasi-steady in time. Fluid flows uniformly over the propeller.
The block only accounts for axial flow across the propeller.
When you set Parameterization to Polynomial fit, the block assumes that the propeller power and thrust coefficients are symmetric with the first quadrant.
When you set Parameterization to Tabulated data for advance ratio, the block assumes the power and thrust coefficients are identical in the first and third quadrants and the second and fourth quadrants. If all elements of J are positive, then the block assumes the coefficients in all quadrants are symmetric with the first quadrant.
When you set Parameterization to Tabulated data for advance angle, the block removes the sign from V_a. To attain negative thrusts and torques, you must include the signs in the values of C_T and C_Q.

Variables

To set the priority and initial target values for the block variables prior to simulation, use the Initial Targets section in the block dialog box or Property Inspector. For more information, see Set Priority and Initial Target for Block Variables.

Nominal values provide a way to specify the expected magnitude of a variable in a model. Using system scaling based on nominal values increases the simulation robustness. Nominal values can come from different sources, one of which is the Nominal Values section in the block dialog box or Property Inspector. For more information, see Modify Nominal Values for a Block Variable.

Examples

Helicopter Transmission

A fixed helicopter transmission testbed. The gasoline engine provides power that is sent to the main and tail rotors through planetary gearsets. The main rotor shaft is considered rigid, and flexibility is modeled in the longer, thinner tail rotor shaft. Blade pitch angle is set directly via a physical signal. Swash plate dynamics can be added using the appropriate blocks in Simscape™ Fluids™. The engine stalls after six seconds, but lift is maintained for some time through the unidirectional clutch. This scheme also allows autorotation of the main rotor in a descending helicopter.

Open Model

Ports

Inputs

expand all

Va — Advance velocity, m/s
physical signal

Physical signal input port associated with the speed of the flow through the propeller, in m/s.

Dependencies

To enable this port, set Translational connections to Physical signals.

θ — Blade pitch, deg
physical signal

Physical signal input port associated with the blade pitch, in degrees.

Dependencies

To enable this port, set Blade pitch type to Controlled.

Rho — Variable density, kg/m^3
physical signal

Physical signal input port associated with the fluid density, in kg/m³.

Dependencies

To enable this port, set Fluid density specification to Variable.

w — Propeller rotational velocity, rad/s
physical signal

Physical signal port associated with the propeller rotational velocity, in rad/s.

Dependencies

To enable this port, set Rotational connections to Physical signals.

Outputs

expand all

Th — Propeller thrust, N
physical signal

Physical signal output port associated with the thrust generated by the propeller, in N.

Dependencies

To enable this port, set Translational connections to Physical signals.

E — Efficiency, unitless
physical signal

Physical signal output port associated with the efficiency of the propeller. The efficiency signal is a function of the absolute value of the advance ratio.

Dependencies

To enable this port, select Efficiency sensor.

Q — Propeller resistive drag, N*m
physical signal

Physical signal port associated with the propeller resistive drag, in N*m.

Dependencies

To enable this port, set Rotational connections to Physical signals.

Conserving

expand all

R1 — Rod interface
mechanical rotational

Mechanical rotational conserving port associated with the rod interface.

Dependencies

To enable this port, set Rotational connections to Conserving.

R2 — Vehicle velocity and thrust
mechanical translational

Mechanical translational conserving port associated with the vehicle velocity and thrust.

Dependencies

To enable this port, set Translational connections to Conserving.

C2 — Reference flow
mechanical translational

Mechanical translational conserving port associated with the motion of the air or wind that the propeller pushes against.

Dependencies

To enable this port, set Translational connections to Conserving.

Parameters

expand all

Propeller

Parameterization — Propeller parameterization
`Constant coefficients` (default) | `Polynomial fit` | `Tabulated data for advance ratio` | `Tabulated data for advance angle` | `Tabulated data for airfoil lift and drag coefficients`

Option to parameterize the propeller by constant, polynomial, tabulated thrust and power coefficients, or tabulated lift and drag coefficients. Choose from these settings:

Constant coefficients — Use constant coefficients of thrust and power with respect to the advance ratio.
Polynomial fit — Use polynomial coefficients to parameterize the advance ratio.
Tabulated data for advance ratio — Use tabulated advance ratio data to parameterize the advance ratio.
Tabulated data for advance angle — Use thrust and power coefficients with respect to the relative advance velocity at 70% of the blade radius.
Tabulated data for airfoil lift and drag coefficients — Use lift and drag coefficients with respect to the position along the blade.

Propeller direction — Propeller direction
`Negative rotational velocity generates positive thrust for positive thrust coefficients` (default) | `Positive rotational velocity generates positive thrust for positive thrust coefficients`

Direction of typical propeller rotation. When you select:

Positive rotational velocity generates positive thrust for positive thrust coefficients — ε = +1.
Negative rotational velocity generates positive thrust for positive thrust coefficients — ε = -1.

Propeller diameter — Propeller diameter
`0.254` `m` (default) | positive scalar

Diameter of the propeller.

Blade pitch type — Constant or controllable blade pitch
`Constant` (default) | `Controlled`

Type of blade to model. Select Constant for a blade with constant pitch or Controlled for a blade with variable pitch that you specify using the θ port.

Dependencies

To enable this parameter, set Parameterization to

Polynomial fit
Tabulated data for advance ratio
Tabulated data for advance angle
Tabulated data for airfoil lift and drag coefficients

Thrust coefficient, kT — Coefficient of thrust
`0.25` (default) | positive scalar

Nondimensional constant thrust coefficient.

Dependencies

To enable this parameter, set Parameterization to Constant coefficients.

Power coefficient, kP — Coefficient of power
`0.13` (default) | positive scalar

Nondimensional constant power coefficient.

kT polynomial coefficients (pN...p0) — Coefficient of thrust polynomial coefficients
`[.002, .0006, -.0509, .0617]` (default) | vector

Vector of nondimensional polynomial thrust coefficients. Specify the elements in descending order. The block uses these coefficients to generate a lookup table. For more information, see Using Lookup Tables in Equations.

Dependencies

To enable this parameter, set:

Parameterization to Polynomial fit
Blade pitch type to Constant

kP polynomial coefficients (pN...p0) — Coefficient of power polynomial coefficients
`[-.0752, .0577, -.0622, .16]` (default) | vector

Vector of nondimensional polynomial power coefficients. Specify the elements in descending order. The block uses these coefficients to generate a lookup table. For more information, see Using Lookup Tables in Equations.

Dependencies

To enable this parameter, set:

Parameterization to Polynomial fit
Blade pitch type to Constant

Pitch angle vector, θ — Pitch angle
`[-15, 15, 25, 35, 45]` `deg` (default) | vector of elements in the range [-360,360]

Reference pitch angles when Blade type is Controlled.

Dependencies

To enable this parameter, set:

Parameterization to Polynomial fit, Tabulated data for advance ratio, or Tabulated data for advance angle
Blade pitch type to Controlled

Table of kT polynomial coefficients (θ, pN...p0) — Polynomial thrust coefficients for controllable pitch propellers
`[.0002, -.00041, -.036, .03; .00026, -.00056, -.048, .04; .002, .00063, -.051, .062; .0014, -.0016, -.048, .087; .00087, -.0036, -.041, .12]` (default) | matrix

Table of polynomial thrust coefficient vectors for the given θ in the Pitch angle vector, θ parameter.

Dependencies

To enable this parameter, set:

Parameterization to Tabulated data for advance ratio
Blade pitch type to Controlled

Table of kP polynomial coefficients (θ, pN...p0) — Polynomial power coefficients for controllable pitch propellers
`[-.1, .031, .0055, .088; -.081, -.025, .0044, .07; -.075, .058, -.062, .16; -.052, .065, -.08, .3; -.031, .057, -.069, .4]` (default) | matrix

Table of polynomial torque coefficient vectors for the given θ in the Pitch angle vector, θ parameter.

Dependencies

To enable this parameter, set:

Parameterization to Tabulated data for advance ratio
Blade pitch type to Controlled

Advance ratio vector, J — Range of advance ratios for tabulated thrust and power coefficients
`[.01, .3, .625, 1.55, 2, 2.6]` (default) | vector

Tabulated advance ratios. Each element has a corresponding element in the Thrust coefficient vector, kT(J) and Power coefficient vector, kP(J) parameters or a column in the Thrust coefficient table, kT(θ, J) and Power coefficient table, kT(θ, J) parameters.

Dependencies

To enable this parameter, set Parameterization to Tabulated coefficients.

Thrust coefficient vector, kT(J) — Tabulated thrust coefficient values for given advance ratio
`[.0614, .0473, .0318, -.0127, -.0343, -.063]` (default) | vector

Tabulated thrust coefficient values as a function of the advance ratio.

Dependencies

To enable this parameter, set:

Parameterization to Tabulated data for advance ratio
Blade pitch type to Constant

Power coefficient vector, kP(J) — Tabulated power coefficient values for given advance ratio
`[.1496, .1314, .116, -.0521, -.1503, -.2813]` (default) | vector

Tabulated power coefficient values as a function of the advance ratio.

Dependencies

To enable this parameter, set:

Parameterization to Tabulated data for advance ratio
Blade pitch type to Constant

Thrust coefficient table, kT(θ, J) — Tabulated thrust coefficient values for given pitch angle and advance ratio
`[.00019, .013, .0048, -.017, -.03, -.045;` (default) | matrix | ...

Tabulated thrust coefficient values as a function of the pitch angle and the advance ratio. The columns correspond to the elements in the Advance ratio vector, J parameter and the rows correspond to the elements in the Pitch angle vector, θ parameter.

The default value is [.00019, .013, .0048, -.017, -.03, -.045; .00039, .025, .0096, -.037, -.06, -.09; .00061, .047, .032, -.013, -.034, -.063; .00086, .072, .057, .014, -.0076, -.036; .12, .104, .09, .049, .029, .0019].

Dependencies

To enable this parameter, set:

Parameterization to Tabulated data for advance ratio
Blade pitch type to Controlled

Power coefficient table, kP(θ, J) — Tabulated power coefficient values for given pitch angle and advance ratio
`[.029, .029, .016, .06, .009, -.16;` (default) | matrix | ...

Tabulated power coefficient values as a function of the pitch angle and the advance ratio. The columns correspond to the elements in the Advance ratio vector, J parameter and the rows correspond to the elements in the Pitch angle vector, θ parameter.

The default value is [.029, .029, .016, .06, .009, -.16; .059, .054, .031, -.12, -.19, -.29; .15, .13, .12, -.052, -.15, -.28; .26, .24, .22, .097, -.04, -.25; .39, .39, .38, .32, .24, .062].

Dependencies

To enable this parameter, set:

Parameterization to Tabulated data for advance ratio
Blade pitch type to Controlled

Advance angle vector, β — Rising advance angles
`linspace(0, 360, 10)` `deg` (default) | vector of length N

Tabulated advance angles. Use a monotonically increasing vector where the elements are in the range [0, 360] deg. During simulation, the propeller advance angle can be in the range [0, 360) deg, where the block wraps the angle between 0 and 360 degrees.

When you set Extrapolation method to Linear or Nearest:

If the first element is not 0, then the block extrapolates based on the first one or two elements when β is less than the first element.
If the last element is not equivalent to 360 deg, then the block extrapolates nased on the last one or two elements when β is greater than the last element.

Dependencies

To enable this parameter, set Parameterization to Tabulated data for advance angle.

Thrust coefficient vector, Ct(β) — Tabulated thrust coefficients for given advance angle
`0.035 * sind(linspace(0, 360, 10) - 200)` (default) | vector of length N

Tabulated thrust coefficients as a function of the advance angle. This coefficient depends on the blade relative advance velocity at 70% of the blade radius. The elements in this vector must correspond one-to-one with the Advance angle vector, β parameter.

Dependencies

To enable this parameter, set Parameterization to Tabulated data for advance angle and set Blade pitch type to Constant.

Torque coefficient vector, Cq(β) — Tabulated torque coefficients for given advance angle
`0.010 * sind(linspace(0, 360, 10) - 200)` (default) | vector of length N

Tabulated resistive torque coefficient as a function of advance angle. This coefficient is based on blade relative advance velocity at 70% of the blade radius. The elements in this vector must correspond one-to-one with the Advance angle vector, β parameter.

Dependencies

To enable this parameter, set Parameterization to Tabulated data for advance angle and set Blade pitch type to Constant.

Thrust coefficient table, Ct(θ, β) — Tabulated thrust coefficients for given pitch angle and advance angle
`[0.01 * sind(linspace(0, 360, 10) - 200); 0.020 * sind(linspace(0, 360, 10) - 200);` (default) | matrix | ...

Tabulated thrust coefficients as a function of pitch angle and advance angle. The default value is [0.01 * sind(linspace(0, 360, 10) - 200); 0.020 * sind(linspace(0, 360, 10) - 200); 0.035 * sind(linspace(0, 360, 10) - 200); 0.04 * sind(linspace(0, 360, 10) - 200); 0.06 * sind(linspace(0, 360, 10) - 200)].

Dependencies

To enable this parameter, set Parameterization to Tabulated data for advance angle and set Blade pitch type to Controlled.

Torque coefficient table, Cq(θ, β) — Tabulated torque coefficients for given pitch angle and advance angle
`[0.0005 * sind(linspace(0, 360, 10) - 200); 0.0015 * sind(linspace(0, 360, 10) - 200);` (default) | matrix | ...

Tabulated torque coefficients as a function of pitch angle and advance angle. The default value is [0.0005 * sind(linspace(0, 360, 10) - 200); 0.0015 * sind(linspace(0, 360, 10) - 200); 0.0025 * sind(linspace(0, 360, 10) - 200); 0.0035 * sind(linspace(0, 360, 10) - 200); 0.0045 * sind(linspace(0, 360, 10) - 200)].

Dependencies

To enable this parameter, set Parameterization to Tabulated data for advance angle and set Blade pitch type to Controlled.

Interpolation method — Method of interpolation between breakpoint values
`Linear` (default) | `Smooth`

Method to use for lookup table breakpoint interpolation. The block uses the tablelookup function to model nonlinearity by using array data to map input values to output values:

Linear — Select this option for the lowest computational cost.
Smooth — Select this option to produce a continuous curve with continuous first-order derivatives.

For more information, see tablelookup.

Dependencies

To enable this parameter, set Parameterization to Tabulated data for advance ratio or Tabulated data for advance angle.

Extrapolation method — Method of handling input values that fall outside range of breakpoint data set
`Linear` (default) | `Nearest` | `Error`

Method to use for lookup table breakpoint extrapolation. This method determines the output value when the input value is outside the range specified in the argument list. The block uses the tablelookup function to model nonlinearity by using array data to map input values to output values:

Linear — Select this option to produce a curve with continuous first-order derivatives in the extrapolation region and at the boundary with the interpolation region.
Nearest — Select this option to produce an extrapolation that does not go above the highest point in the data or below the lowest point in the data.
Error — Select this option to avoid extrapolating when you want your data to be within the table range. If the input signal is outside the range of the table, the simulation stops and generates an error.

Dependencies

To enable this parameter, set Parameterization to Tabulated data for advance ratio or Tabulated data for advance angle.

Root pitch angle — Root pitch angle
`20` `deg` (default) | scalar

Constant pitch offset angle of the propeller blades.

Dependencies

To enable this parameter, set Parameterization to Tabulated data for airfoil lift and drag coefficients and Blade pitch type to Constant.

Number of blades — Number of blades
`2` (default) | positive scalar

Number of propeller blades.

Dependencies

To enable this parameter, set Parameterization to Tabulated data for airfoil lift and drag coefficients.

Number of blade elements — Number of blade elements
`20` (default) | positive scalar

Number of blade elements for a single blade.

Dependencies

To enable this parameter, set Parameterization to Tabulated data for airfoil lift and drag coefficients.

Nondimensional radial location vector, r — Radial location
`[.1, .12, .2, .4, .6, .8, 1]` (default) | vector

Radial location for a given set of blade dimensions. 1 is equivalent to the radius of the blade. The first element of this vector defines e, the root cutout.

Dependencies

To enable this parameter, set Parameterization to Tabulated data for airfoil lift and drag coefficients.

Blade twist vector, θ_tw(r) — Blade element twist
`[30, 35, 50, 30, 20, 15, 10]` `deg` (default) | vector

Blade twist angles, θ, for a given radial location. The elements of this vector correspond one-to-one with the Nondimensional radial location vector, r parameter.

Dependencies

To enable this parameter, set Parameterization to Tabulated data for airfoil lift and drag coefficients.

Normalized chord length vector, c(r)/D — Blade element chord length
`[.0676, .0666, .0824, .1025, .0885, .0598, .0133]` (default) | vector of length N

Chord length normalized by diameter for a given radial location along the blade. The elements of this vector correspond one-to-one with the Nondimensional radial location vector, r parameter and the columns of the Airfoil lift coefficient table, Cl(α,r) and Airfoil drag coefficient table, Cd(α,r) parameters.

Dependencies

To enable this parameter, set Parameterization to Tabulated data for airfoil lift and drag coefficients.

Airfoil angle of attack vector, α — Angle of attack
`-180 : 10 : 180` `deg` (default) | vector of length M

Angle of attack range. The elements of this vector correspond one-to-one with the rows of the Airfoil lift coefficient table, Cl(α,r) and Airfoil drag coefficient table, Cd(α,r) parameters.

Dependencies

To enable this parameter, set Parameterization to Tabulated data for airfoil lift and drag coefficients.

Airfoil lift coefficient table, Cl(α,r) — Airfoil lift coefficients
M x N matrix | ...

Airfoil lift coefficients for a given angle of attack and radial location along the blade. The rows in this matrix correspond one-to-one with the Airfoil angle of attack vector, α parameter. The columns in this matrix correspond one-to-one with the Nondimensional radial location vector, r parameter.

The default value is [.1326, .1326, .1274, .1274, .1274, .1274, .1274; .3626, .3626, .5002, .5002, .5002, .5002, .5002; .5528, .5528, .8007, .8007, .8007, .8007, .8007; .7256, .7256, 1.0125, 1.0125, 1.0125, 1.0125, 1.0125; .8016, .8016, 1.1556, 1.1556, 1.1556, 1.1556, 1.1556; .7873, .7873, 1.1604, 1.1604, 1.1604, 1.1604, 1.1604; .7031, .7031, 1.0493, 1.0493, 1.0493, 1.0493, 1.0493; .5423, .5423, .7973, .7973, .7973, .7973, .7973; .3537, .3537, .4332, .4332, .4332, .4332, .4332; .1155, .1155, -.0376, -.0376, -.0376, -.0376, -.0376; -.1045, -.1045, -.4096, -.4096, -.4096, -.4096, -.4096; -.2999, -.2999, -.672, -.672, -.672, -.672, -.672; -.4401, -.4401, -.9343, -.9343, -.9343, -.9343, -.9343; -.5186, -.5186, -1.0477, -1.0477, -1.0477, -1.0477, -1.0477; -.5303, -.5303, -1.0387, -1.0387, -1.0387, -1.0387, -1.0387; -.5073, -.5073, -.9565, -.9565, -.9565, -.9565, -.9565; -.442, -.442, -.7713, -.7713, -.7713, -.7713, -.7713; -.2658, -.2658, -.4832, -.4832, -.4832, -.4832, -.4832; .4109, .4109, .3629, .3629, .3629, .3629, .3629; 1.1635, 1.1635, 1.3779, 1.3779, 1.3779, 1.3779, 1.3779; 1.2412, 1.2412, 1.4033, 1.4033, 1.4033, 1.4033, 1.4033; .7434, .7434, 1.3453, 1.3453, 1.3453, 1.3453, 1.3453; .7908, .7908, 1.2862, 1.2862, 1.2862, 1.2862, 1.2862; .7525, .7525, 1.1562, 1.1562, 1.1562, 1.1562, 1.1562; .6722, .6722, .9487, .9487, .9487, .9487, .9487; .5324, .5324, .7047, .7047, .7047, .7047, .7047; .3365, .3365, .382, .382, .382, .382, .382; .0529, .0529, -.0229, -.0229, -.0229, -.0229, -.0229; -.2728, -.2728, -.316, -.316, -.316, -.316, -.316; -.4135, -.4135, -.6195, -.6195, -.6195, -.6195, -.6195; -.5087, -.5087, -.7847, -.7847, -.7847, -.7847, -.7847; -.5342, -.5342, -.8419, -.8419, -.8419, -.8419, -.8419; -.5166, -.5166, -.7658, -.7658, -.7658, -.7658, -.7658; -.4321, -.4321, -.5707, -.5707, -.5707, -.5707, -.5707; -.2864, -.2864, -.3098, -.3098, -.3098, -.3098, -.3098; -.1073, -.1073, -.0893, -.0893, -.0893, -.0893, -.0893; .1326, .1326, .1274, .1274, .1274, .1274, .1274].

Dependencies

To enable this parameter, set Parameterization to Tabulated data for airfoil lift and drag coefficients.

Airfoil drag coefficient table, Cd(α,r) — Airfoil drag coefficients
M x N matrix | ...

Airfoil drag coefficients for a given angle of attack and radial location along the blade. The rows in this matrix correspond one-to-one with the Airfoil angle of attack vector, α parameter. The columns in this matrix correspond one-to-one with the Nondimensional radial location vector, r parameter.

The default value is [.0055, .0055, .3904, .3904, .3904, .3904, .3904; .0774, .0774, .449, .449, .449, .449, .449; .2412, .2412, .5915, .5915, .5915, .5915, .5915; .4342, .4342, .8307, .8307, .8307, .8307, .8307; .679, .679, 1.0909, 1.0909, 1.0909, 1.0909, 1.0909; .9003, .9003, 1.3868, 1.3868, 1.3868, 1.3868, 1.3868; 1.0825, 1.0825, 1.6565, 1.6565, 1.6565, 1.6565, 1.6565; 1.2281, 1.2281, 1.875, 1.875, 1.875, 1.875, 1.875; 1.3205, 1.3205, 2.017, 2.017, 2.017, 2.017, 2.017; 1.3234, 1.3234, 2.0407, 2.0407, 2.0407, 2.0407, 2.0407; 1.2391, 1.2391, 1.9513, 1.9513, 1.9513, 1.9513, 1.9513; 1.0963, 1.0963, 1.7643, 1.7643, 1.7643, 1.7643, 1.7643; .8978, .8978, 1.5048, 1.5048, 1.5048, 1.5048, 1.5048; .6525, .6525, 1.2281, 1.2281, 1.2281, 1.2281, 1.2281; .4203, .4203, .838, .838, .838, .838, .838; .2428, .2428, .5434, .5434, .5434, .5434, .5434; .0951, .0951, .2517, .2517, .2517, .2517, .2517; .0292, .0292, .0698, .0698, .0698, .0698, .0698; .0148, .0148, .0267, .0267, .0267, .0267, .0267; .0808, .0808, .0509, .0509, .0509, .0509, .0509; .2429, .2429, .1561, .1561, .1561, .1561, .1561; .5019, .5019, .3927, .3927, .3927, .3927, .3927; .7217, .7217, .7438, .7438, .7438, .7438, .7438; .9336, .9336, 1.1277, 1.1277, 1.1277, 1.1277, 1.1277; 1.0984, 1.0984, 1.4838, 1.4838, 1.4838, 1.4838, 1.4838; 1.2274, 1.2274, 1.7877, 1.7877, 1.7877, 1.7877, 1.7877; 1.3016, 1.3016, 1.9779, 1.9779, 1.9779, 1.9779, 1.9779; 1.3305, 1.3305, 2.0516, 2.0516, 2.0516, 2.0516, 2.0516; 1.2889, 1.2889, 1.9974, 1.9974, 1.9974, 1.9974, 1.9974; 1.1677, 1.1677, 1.8463, 1.8463, 1.8463, 1.8463, 1.8463; 1.0076, 1.0076, 1.5699, 1.5699, 1.5699, 1.5699, 1.5699; .8068, .8068, 1.2596, 1.2596, 1.2596, 1.2596, 1.2596; .5688, .5688, .9493, .9493, .9493, .9493, .9493; .3604, .3604, .6154, .6154, .6154, .6154, .6154; .1802, .1802, .5015, .5015, .5015, .5015, .5015; .0699, .0699, .4265, .4265, .4265, .4265, .4265; .0055, .0055, .3904, .3904, .3904, .3904, .3904].

Dependencies

To enable this parameter, set Parameterization to Tabulated data for airfoil lift and drag coefficients.

Environment and Dynamics

Fluid density specification — Fluid density selection
`Constant` (default) | `Variable`

Option to specify a constant or variable fluid density.

Fluid density — Constant fluid density value
`1.225` `kg/m^3` (default)

Constant fluid density value.

Dependencies

To enable this parameter, set Fluid density specification to Constant.

Rotational connections — Rotational motion input option
`Physical signals` (default) | `Conserving`

Option to simulate propeller rotational velocity and resistive drag torque as physical signal inputs and outputs, respectively, or as rotational connections. This setting determines the color of the hub in the icon, which indicates whether the block is in the rotational conserving or physical signal domain.

Translational connections — Translational motion input option
`Conserving` (default) | `Physical signals`

Option to simulate advance velocity and propeller thrust as physical signal inputs and outputs, respectively, or as translational connections. This setting determines the color of the of the blades in the icon, which indicates whether the block is in the translational conserving or physical signal domain. When you select Conserving, the constant wake fraction reduces the advance velocity relative to the vehicle velocity.

Model inertia — Inertia option
`off` (default) | `on`

Whether to simulate inertia due to the motion of the rotor. The block applies rotational inertia at port R1 and translational inertia at port R2.

Dependencies

To enable this parameter, set Rotational connections or Translational connections to conserving.

Propeller inertia — Propeller inertia
`1` `kg*m^2` (default) | positive scalar

Inertia of the propeller assembly. The block applies the inertia at port R1.

Dependencies

To enable this parameter, set Rotational connections to conserving and select Model inertia.

Propeller mass — Propeller mass
`10` `kg` (default) | positive scalar

Mass of the propeller assembly. The block applies the translational inertia at port R2.

Dependencies

To enable this parameter, set Translational connections to conserving and select Model inertia.

Advanced

Efficiency sensor — Operating efficiency output option
`off` (default) | `on`

Whether to enable the efficiency port E, which outputs a positive-valued efficiency signal.

Rotational speed threshold — Rotational speed smoothing point
`0.001` `Hz` (default) | positive scalar

Saturation threshold value, n_Thr, beyond which the block applies smoothing up to the point of saturation.

Saturation threshold for nondimensional coefficients — nondimensional coefficient smoothing point
`0.001` (default) | positive scalar

Saturation threshold value, k_Thr, where the block applies smoothing to nondimensional coefficients.

Check if operating beyond normal propeller operation — Operating bounds tolerance
`Warning` (default) | `None` | `Error`

Whether to generate a warning or error when the propeller exceeds the operating parameters. The block checks whether the propeller is operating in the first quadrant. If either V_a or n(t) are not positive, the propeller generates thrust and torque coefficients with the appropriate signs and a warning or error, depending on the parameter setting. As you raise the value for the Rotational speed threshold parameter, the trigger becomes less sensitive.

When you set Parameterization to Polynomial fit, the block generates a warning or error when the propeller exceeds the first positive root of the k_T parameter.

The block approximates the hydrodynamics using symmetric or asymmetric behavior with respect to the first quadrant.

Dependencies

To enable this parameter, set Parameterization to Polynomial fit or Tabulated data for advance ratio.

Power threshold for efficiency calculation — Power threshold
100 `W` (default)

Power threshold when calculating efficiency.

Dependencies

To enable this parameter, set Parameterization to Tabulated data for airfoil lift and drag coefficients and select Efficiency sensor.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced in R2022b

expand all

R2023b: Parameterize by lift and drag coefficients

To parameterize the block by tabulated lift and drag coefficients along the propeller, set Parameterization to Tabulated data for airfoil lift and drag coefficients.

R2023a: Performance updates

Port C1 is no longer required and has been removed.

R2023a: New inertia option

To model inertia, select Model inertia and set Rotational connections or Translational connections to Conserving to enable the Propeller inertia or Propeller mass parameters, respectively.

Aerodynamic Propeller

Description

Parameterizations

Inertia

Assumptions and Limitations

Variables

Examples

Helicopter Transmission

Ports

Inputs

Va — Advance velocity, m/s physical signal

Dependencies

θ — Blade pitch, deg physical signal

Dependencies

Rho — Variable density, kg/m^3 physical signal

Dependencies

w — Propeller rotational velocity, rad/s physical signal

Dependencies

Outputs

Th — Propeller thrust, N physical signal

Dependencies

E — Efficiency, unitless physical signal

Dependencies

Q — Propeller resistive drag, N*m physical signal

Dependencies

Conserving

R1 — Rod interface mechanical rotational

Dependencies

R2 — Vehicle velocity and thrust mechanical translational

Dependencies

C2 — Reference flow mechanical translational

Dependencies

Parameters

Propeller

Parameterization — Propeller parameterization Constant coefficients (default) | Polynomial fit | Tabulated data for advance ratio | Tabulated data for advance angle | Tabulated data for airfoil lift and drag coefficients

Propeller direction — Propeller direction Negative rotational velocity generates positive thrust for positive thrust coefficients (default) | Positive rotational velocity generates positive thrust for positive thrust coefficients

Propeller diameter — Propeller diameter 0.254 m (default) | positive scalar

Blade pitch type — Constant or controllable blade pitch Constant (default) | Controlled

Dependencies

Thrust coefficient, kT — Coefficient of thrust 0.25 (default) | positive scalar

Dependencies

Power coefficient, kP — Coefficient of power 0.13 (default) | positive scalar

kT polynomial coefficients (pN...p0) — Coefficient of thrust polynomial coefficients [.002, .0006, -.0509, .0617] (default) | vector

Dependencies

kP polynomial coefficients (pN...p0) — Coefficient of power polynomial coefficients [-.0752, .0577, -.0622, .16] (default) | vector

Dependencies

Pitch angle vector, θ — Pitch angle [-15, 15, 25, 35, 45] deg (default) | vector of elements in the range [-360,360]

Dependencies

Table of kT polynomial coefficients (θ, pN...p0) — Polynomial thrust coefficients for controllable pitch propellers [.0002, -.00041, -.036, .03; .00026, -.00056, -.048, .04; .002, .00063, -.051, .062; .0014, -.0016, -.048, .087; .00087, -.0036, -.041, .12] (default) | matrix

Dependencies

Table of kP polynomial coefficients (θ, pN...p0) — Polynomial power coefficients for controllable pitch propellers [-.1, .031, .0055, .088; -.081, -.025, .0044, .07; -.075, .058, -.062, .16; -.052, .065, -.08, .3; -.031, .057, -.069, .4] (default) | matrix

Dependencies

Advance ratio vector, J — Range of advance ratios for tabulated thrust and power coefficients [.01, .3, .625, 1.55, 2, 2.6] (default) | vector

Dependencies

Thrust coefficient vector, kT(J) — Tabulated thrust coefficient values for given advance ratio [.0614, .0473, .0318, -.0127, -.0343, -.063] (default) | vector

Dependencies

Power coefficient vector, kP(J) — Tabulated power coefficient values for given advance ratio [.1496, .1314, .116, -.0521, -.1503, -.2813] (default) | vector

Dependencies

Thrust coefficient table, kT(θ, J) — Tabulated thrust coefficient values for given pitch angle and advance ratio [.00019, .013, .0048, -.017, -.03, -.045; (default) | matrix | ...

Dependencies

Power coefficient table, kP(θ, J) — Tabulated power coefficient values for given pitch angle and advance ratio [.029, .029, .016, .06, .009, -.16; (default) | matrix | ...

Dependencies

Advance angle vector, β — Rising advance angles linspace(0, 360, 10) deg (default) | vector of length N

Dependencies

Thrust coefficient vector, Ct(β) — Tabulated thrust coefficients for given advance angle 0.035 * sind(linspace(0, 360, 10) - 200) (default) | vector of length N

Dependencies

Torque coefficient vector, Cq(β) — Tabulated torque coefficients for given advance angle 0.010 * sind(linspace(0, 360, 10) - 200) (default) | vector of length N

Dependencies

Thrust coefficient table, Ct(θ, β) — Tabulated thrust coefficients for given pitch angle and advance angle [0.01 * sind(linspace(0, 360, 10) - 200); 0.020 * sind(linspace(0, 360, 10) - 200); (default) | matrix | ...

Dependencies

Torque coefficient table, Cq(θ, β) — Tabulated torque coefficients for given pitch angle and advance angle [0.0005 * sind(linspace(0, 360, 10) - 200); 0.0015 * sind(linspace(0, 360, 10) - 200); (default) | matrix | ...

Dependencies

Interpolation method — Method of interpolation between breakpoint values Linear (default) | Smooth

Dependencies

Extrapolation method — Method of handling input values that fall outside range of breakpoint data set Linear (default) | Nearest | Error

Dependencies

Root pitch angle — Root pitch angle 20 deg (default) | scalar

Dependencies

Number of blades — Number of blades 2 (default) | positive scalar

Dependencies

Va — Advance velocity, m/s
physical signal

θ — Blade pitch, deg
physical signal

Rho — Variable density, kg/m^3
physical signal

w — Propeller rotational velocity, rad/s
physical signal

Th — Propeller thrust, N
physical signal

E — Efficiency, unitless
physical signal

Q — Propeller resistive drag, N*m
physical signal

R1 — Rod interface
mechanical rotational

R2 — Vehicle velocity and thrust
mechanical translational

C2 — Reference flow
mechanical translational

Parameterization — Propeller parameterization
`Constant coefficients` (default) | `Polynomial fit` | `Tabulated data for advance ratio` | `Tabulated data for advance angle` | `Tabulated data for airfoil lift and drag coefficients`

Propeller direction — Propeller direction
`Negative rotational velocity generates positive thrust for positive thrust coefficients` (default) | `Positive rotational velocity generates positive thrust for positive thrust coefficients`

Propeller diameter — Propeller diameter
`0.254` `m` (default) | positive scalar

Blade pitch type — Constant or controllable blade pitch
`Constant` (default) | `Controlled`

Thrust coefficient, kT — Coefficient of thrust
`0.25` (default) | positive scalar

Power coefficient, kP — Coefficient of power
`0.13` (default) | positive scalar

kT polynomial coefficients (pN...p0) — Coefficient of thrust polynomial coefficients
`[.002, .0006, -.0509, .0617]` (default) | vector

kP polynomial coefficients (pN...p0) — Coefficient of power polynomial coefficients
`[-.0752, .0577, -.0622, .16]` (default) | vector

Pitch angle vector, θ — Pitch angle
`[-15, 15, 25, 35, 45]` `deg` (default) | vector of elements in the range [-360,360]

Table of kT polynomial coefficients (θ, pN...p0) — Polynomial thrust coefficients for controllable pitch propellers
`[.0002, -.00041, -.036, .03; .00026, -.00056, -.048, .04; .002, .00063, -.051, .062; .0014, -.0016, -.048, .087; .00087, -.0036, -.041, .12]` (default) | matrix

Table of kP polynomial coefficients (θ, pN...p0) — Polynomial power coefficients for controllable pitch propellers
`[-.1, .031, .0055, .088; -.081, -.025, .0044, .07; -.075, .058, -.062, .16; -.052, .065, -.08, .3; -.031, .057, -.069, .4]` (default) | matrix

Advance ratio vector, J — Range of advance ratios for tabulated thrust and power coefficients
`[.01, .3, .625, 1.55, 2, 2.6]` (default) | vector

Thrust coefficient vector, kT(J) — Tabulated thrust coefficient values for given advance ratio
`[.0614, .0473, .0318, -.0127, -.0343, -.063]` (default) | vector

Power coefficient vector, kP(J) — Tabulated power coefficient values for given advance ratio
`[.1496, .1314, .116, -.0521, -.1503, -.2813]` (default) | vector

Thrust coefficient table, kT(θ, J) — Tabulated thrust coefficient values for given pitch angle and advance ratio
`[.00019, .013, .0048, -.017, -.03, -.045;` (default) | matrix | ...

Power coefficient table, kP(θ, J) — Tabulated power coefficient values for given pitch angle and advance ratio
`[.029, .029, .016, .06, .009, -.16;` (default) | matrix | ...

Advance angle vector, β — Rising advance angles
`linspace(0, 360, 10)` `deg` (default) | vector of length N

Thrust coefficient vector, Ct(β) — Tabulated thrust coefficients for given advance angle
`0.035 * sind(linspace(0, 360, 10) - 200)` (default) | vector of length N

Torque coefficient vector, Cq(β) — Tabulated torque coefficients for given advance angle
`0.010 * sind(linspace(0, 360, 10) - 200)` (default) | vector of length N

Thrust coefficient table, Ct(θ, β) — Tabulated thrust coefficients for given pitch angle and advance angle
`[0.01 * sind(linspace(0, 360, 10) - 200); 0.020 * sind(linspace(0, 360, 10) - 200);` (default) | matrix | ...

Torque coefficient table, Cq(θ, β) — Tabulated torque coefficients for given pitch angle and advance angle
`[0.0005 * sind(linspace(0, 360, 10) - 200); 0.0015 * sind(linspace(0, 360, 10) - 200);` (default) | matrix | ...

Interpolation method — Method of interpolation between breakpoint values
`Linear` (default) | `Smooth`

Extrapolation method — Method of handling input values that fall outside range of breakpoint data set
`Linear` (default) | `Nearest` | `Error`

Root pitch angle — Root pitch angle
`20` `deg` (default) | scalar

Number of blades — Number of blades
`2` (default) | positive scalar

Number of blade elements — Number of blade elements
`20` (default) | positive scalar

Nondimensional radial location vector, r — Radial location
`[.1, .12, .2, .4, .6, .8, 1]` (default) | vector

Blade twist vector, θ_tw(r) — Blade element twist
`[30, 35, 50, 30, 20, 15, 10]` `deg` (default) | vector

Normalized chord length vector, c(r)/D — Blade element chord length
`[.0676, .0666, .0824, .1025, .0885, .0598, .0133]` (default) | vector of length N

Airfoil angle of attack vector, α — Angle of attack
`-180 : 10 : 180` `deg` (default) | vector of length M

Airfoil lift coefficient table, Cl(α,r) — Airfoil lift coefficients
M x N matrix | ...

Airfoil drag coefficient table, Cd(α,r) — Airfoil drag coefficients
M x N matrix | ...

Fluid density specification — Fluid density selection
`Constant` (default) | `Variable`

Fluid density — Constant fluid density value
`1.225` `kg/m^3` (default)

Rotational connections — Rotational motion input option
`Physical signals` (default) | `Conserving`

Translational connections — Translational motion input option
`Conserving` (default) | `Physical signals`

Model inertia — Inertia option
`off` (default) | `on`

Propeller inertia — Propeller inertia
`1` `kg*m^2` (default) | positive scalar

Propeller mass — Propeller mass
`10` `kg` (default) | positive scalar

Efficiency sensor — Operating efficiency output option
`off` (default) | `on`

Rotational speed threshold — Rotational speed smoothing point
`0.001` `Hz` (default) | positive scalar

Saturation threshold for nondimensional coefficients — nondimensional coefficient smoothing point
`0.001` (default) | positive scalar

Check if operating beyond normal propeller operation — Operating bounds tolerance
`Warning` (default) | `None` | `Error`

Power threshold for efficiency calculation — Power threshold
100 `W` (default)

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.