Minimal Cascade Model for a Mitotic Oscillator

Albert Goldbeter modified a model with enzyme cascades [Goldbeter and Koshland 1981] to fit cell cycle data from studies with embryonic cells [Goldbeter 1991]. He used this model to demonstrate thresholds with enzyme cascades and periodic behavior caused by negative feedback.

There are two SimBiology^® model variations using Goldbeter's model. The first model uses the differential rate equations directly from Goldbeter's paper. The second model is built with reactions using Henri-Michaelis-Menten kinetics.

Goldbeter Model
SimBiology Model with Rate Rules
SimBiology Model with Reactions
References

Goldbeter Model

About the Goldbeter Model
Reaction Descriptions and Model Assumptions
Mathematical Model

About the Goldbeter Model

Albert Goldbeter created a simple cell division model from studies with embryonic cells [Goldbeter 1991]. This model demonstrates thresholds with enzyme cascades and periodic behavior caused by negative feedback.

There are six species in Goldbeter's minimal mitotic oscillator model [Goldbeter 1991].

C — Cyclin. The periodic behavior of cyclin activates and deactivates an enzyme cascade.
M+, M — Inactive (phosphorylated) and active forms of cdc2 kinase. Kinases catalyze the addition of phosphate groups onto amino acid residues.
X+, X — Inactive and active (phosphorylated) forms of a cyclin protease. Proteases degrade proteins by breaking peptide bonds.

The reactions are labeled r1 to r7 on the following diagram.

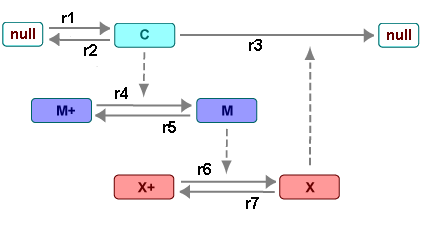
This model shows:

How thresholds with cdc2 kinase activation (M+ -> M) and protease activation (X+ -> X) can occur as the result of covalent modification (for example, phosphorylation or dephosphorylation), but without the need for positive feedback.
How periodic behavior with cdc2 kinase activation can occur with negative feedback and the time delay associated with activation/deactivation enzyme cascades.

Reaction Descriptions and Model Assumptions

The following list describes each of the reactions in Goldbeter's minimal mitotic oscillator with some of the simplifying assumptions. For a more detailed explanation of the model, see [Goldbeter 1991].

Cyclin (C) is synthesized at a constant rate (r1) and degraded at a constant rate (r2).
Cyclin (C) does not complex with cdc2 kinase (M).
Cyclin (C) activates cdc2 kinase (M+ -> M) by increasing the velocity of the phosphatase that activates the kinase. Inactive cdc2 kinase (M+) is activated by removing inhibiting phosphate groups (r4).
The amount of deactivating kinase (not modeled) for the cdc2 kinase (M) is constant. Active cdc2 kinase (M) is deactivated by adding inhibiting phosphate group (r5).
The activation of cyclin protease (X+ -> X) by the active cdc2 kinase (M) is direct without other intervening cascades. Cyclin protease (X) is activated by adding phosphate groups (r6).
The amount of deactivating phosphatase (not modeled) for the cyclin protease (X) is constant. Active cyclin protease (X) is deactivated by removing the activating phosphate groups (r7).
The three species of interest are cyclin (C), active dephosphorylated cdc2 kinase (M), and active phosphorylated protease (X). The total amounts of (M + M+) and (X + X+) are constant.

Mathematical Model

Goldbeter's minimal mitotic oscillator model is defined with three differential rate equations and two algebraic equations that define changing parameters in the rate equations.

Differential Rate Equation 1, Cyclin (C). The following differential rate equation is from [Goldbeter 1991] for cyclin (C).

$\frac{d C}{d t} = v_{i} - v_{d} X \frac{C}{K_{d} + C} - k_{d} C$

Differential Rate Equation 2, Kinase (M). The following differential rate equation is for cdc2 kinase (M). Notice that (1 - M) is the amount of inactive (phosphorylated) cdc2 kinase (M+).

$\frac{d M}{d t} = V_{1} \frac{(1 - M)}{K_{1} + (1 - M)} - V_{2} \frac{M}{K_{2} + M}$

$V_{1} = \frac{V M_{1} [C]}{K_{c} + [C]}$

Differential Rate Equation 3, Protease (X). Differential rate equations for cyclin protease (X). Notice that (1 - X) is the amount of inactive (unphosphorylated) cyclin protease (X+).

$\frac{d X}{d t} = V_{3} \frac{(1 - X)}{K_{3} + (1 - X)} - V_{4} \frac{X}{K_{4} + X}$

$V_{3} = V M_{3} [M]$

Load Goldbeter Model with Rules

Open Live Script

Enter the following command to open the rule-based minimal cascade model for a mitotic oscillator (Goldbeter model).

openExample('simbio/GoldbeterWithRulesSimBiologyExample')

SimBiology Model with Rules

In the literature, many biological models are defined using differential rate and algebraic equations. With SimBiology software, you can enter the equations directly as SBML rules. The example in this section uses Goldbeter's mitotic oscillator to illustrate this point.

Writing differential rate equations in an unambiguous format that a software program can understand is a fairly simple process.

Use an asterisk to indicate multiplication. For example, k[a] is written k*a.
Remove square brackets that indicate concentration from around species. The units associated with the species will indicate concentration (moles/liter) or amount (moles, molecules).
SimBiology software uses square brackets around species and parameter name to allow names that are not valid MATLAB^® variable names. For example, you could have a species named glucose-6-phosphate dehydrogenase but you need to add brackets around the name in reaction rate and rule equations.
Use parentheses to clarify the order of evaluation for mathematical operations. For example, do not write a Henri-Michaelis-Menten rate as Vm*C/Kd + C, because Vm*C is divided by Kd before adding C, and then C is added to the result.

The following equation is the rate rule for Differential Rate Equation 1, Cyclin (C):

dC/dt = vi - (vd*X*C)/(Kd + C) - kd*C

The following equations are the rate and repeatedAssignment rules for Differential Rate Equation 2, Kinase (M):

dM/dt = (V1*Mplus)/(K1 + Mplus) - (V2*M)/(K2 + M)
V1 = (VM1*C)/(Kc + C)
Mplus = Mt - M

The following equations are the rate and repeatedAssignment rules for Differential Rate Equation 3, Protease (X):

dX/dt = (V3*Xplus)/(K3 + Xplus) - (V4*X)/(K4 + X)
V3 = VM3*M
Xplus = Xt - X

Rules. The active (M) and inactive (Mplus) forms of the kinase are assumed to be part of a conserved cycle with the total concentration (Mt) remaining constant during the simulation. You need only one differential rate equation with a mass balance equation to define the amounts of both species. Similarly, the active (X) and inactive (Xplus) forms of the protease are part of a second conserved cycle.

SimBiology Simulation with Rules

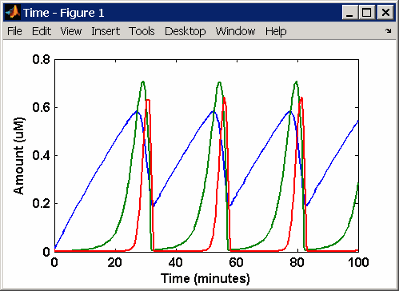
This is a simulation of Goldbeter's minimal mitotic oscillator using differential rate and algebraic equations. Simulate with the sundials solver and plot species C, M, and X. For a description of the model, see SimBiology Model with Rules.

SimBiology Model with Reactions

Load Goldbeter Model with Reactions
Converting Differential Rate Equations to Reactions
Calculating Initial Values for Reactions
SimBiology Simulation with Reactions

Load Goldbeter Model with Reactions

Open Live Script

Enter the following command to open the reaction-based minimal cascade model for a mitotic oscillator (Goldbeter model).

openExample('simbio/GoldbeterWithReactionsSimBiologyExample')

Converting Differential Rate Equations to Reactions

In the literature, many models are defined with differential rate equations. With SimBiology software, creating the differential equations from reactions is unnecessary; you can enter the reactions and let the software calculate the equations.

Some models are defined with differential rate equations, and you might need the reactions to be compatible with your model. Two rules you can use to convert differential rate equations to reactions are:

For a positive term — The species described by the equation is placed on the right as a product, and the species in the term are placed on the left as reactants.
For a negative term — The species described by the equation is placed on the left as a product, and the species in the term are also placed on the left as reactants.
You need to determine the products using additional information, for example, a reaction diagram, a description of the model, or an understanding of a reaction. If a reaction is catalyzed by a kinase, then you can conclude that the product has one or more additional phosphate groups.

A simple first-order reaction has differential rate equation dR/dt = +kr[P] - kf[R]. The negative term implies that the reaction is R -> ? with an unknown product. The positive term identifies the product and completes the reaction, R <-> P.

Reactions R1 to R3 from Equation E1. The differential rate equation 1 is repeated here for comparison with the reactions. See Differential Rate Equation 1, Cyclin (C).

 $\frac{d C}{d t} = v_{i} - v_{d} X \frac{C}{K_{d} + C} - k_{d} C$

The reaction and reaction rate equations from the differential rate equation E1 are given below:

r1      reaction: null -> C
   reaction rate: vi 

r2      reaction: C -> null
   reaction rate: kd*C

r3      reaction: C -> null
   reaction rate: (vd*X*C)/(Kd + C)

Reactions R4 and R5 from Equation E2. The differential rate equation 2 and algebraic equation 2 are repeated here for comparison with the reactions. See Differential Rate Equation 2, Kinase (M).

$\frac{d M}{d t} = V_{1} \frac{(1 - M)}{K_{1} + (1 - M)} - V_{2} \frac{M}{K_{2} + M}$

$V_{1} = \frac{V M_{1} [C]}{K_{c} + [C]}$

The reaction and reaction rate equations from the differential rate equation E2 are given below:

r4              reaction: Mplus -> M
           reaction rate: V1*Mplus/(K1 + Mplus)
 repeatedAssignment rule: V1 = VM1*C/(Kc + C)

r5      reaction: M -> Mplus
   reaction rate: V2*M/(K2 + M)

Reactions R6 and R7 from Equation E3. The differential rate equation for equation 3 and algebraic equation 3 is repeated here for comparison with the reactions.

$\frac{d X}{d t} = V_{3} \frac{(1 - X)}{K_{3} + (1 - X)} - V_{4} \frac{X}{K_{4} + X}$

V3 = VM3*[M]

The reaction and reaction rate equations from the differential rate equation E3 are given below:

r6               reaction: Xplus -> X
            reaction rate: V3*Xplus]/(K3 + Xplus)
  repeatedAssignment rule: V3 = VM3*M

r7      reaction: X -> Xplus
   reaction rate: V4*X/(K4 + X)

Calculating Initial Values for Reactions

After you converted the differential rate equations to the reactions and reaction rate equations, you can start to fill in initial values for the species (reactants and products) and parameters.

The initial values for parameters and amounts for species are listed with four different units in the same dimension:

A — Original units in the Goldbeter 1991 paper.
B — Units of concentration with time converted to second. When converting a to b, use 1 minute = 60 second for parameters.
$\frac{X uM}{minute} x \frac{1e-6 mole/liter}{1 uM} x \frac{1 minute}{60 second} = \frac{Y mole}{liter*second}$
C — Units of amount as moles. When converting concentration to moles, use a cell volume of 1e-12 liter and assume that volume does not change.
$\frac{Y mole}{liter*second} x \frac{1e-12 liter}{} = \frac{Z mole}{second}$
D — Units of amount as molecules. When converting amount as moles to molecules, use 6.022e23 molecules = 1 mole.
$\frac{Z mole}{second} x \frac{6 .022e23 molecule}{1 mole} = \frac{N molecules}{second}$

With dimensional analysis on and unit conversion off, select all of the units for one letter. For example, select all of the As. If dimensional analysis and unit conversion are on, you can mix and match letters and get the same answer.

Reaction 1 Cyclin Synthesis

R1		Value	Units
reaction	null -> C	----	----
reaction rate	vi	----	A. uM/minute
		----	B. mole/(liter*second)
		----	C. mole/second
		----	D. molecule/second
parameters	vi	0.025	A. uM/minute
		4.167e-10	B. mole/(liter*second)
		4.167e-22	C. mole/second
		205	D. molecule/second
species	C	0.01	A. uM
		1e-8	B. mole/liter
		1.0e-20	C. mole
		6.022e+3	D. molecule

Reaction 2 Cyclin Undifferentiated Degradation

R2		Value	Units
reaction	`C -> null`	----	----
reaction rate	`kd*C`	----	A. uM/minute
		----	B. mole/(liter*second)
		----	C. mole/second
		----	D. molecule/second
parameters	`kd`	0.010	A. 1/minute
		1.6667e-4	B, C, D. 1/second
species	`C`	0.01	A. uM
		1e-8	B. mole/liter
		1.0e-20	C. mole
		6.022e+3	D. molecule

Reaction 3 Cyclin Protease Degradation

R3		Value	Units
reaction	`C -> null`	----	----
reaction rate	`(vdXC)/(Kd + C)`	----	A. uM/minute
		----	B. mole/(liter*second)
		----	C. mole/second
		----	D. molecule/second
parameter	`vd`	0.25	A. 1/minute
		0.0042	B, C, D. 1/second
parameter	`Kd`	0.02	A. uM
		2.0e-8	B. mole/liter
		2.0e-020	C. mole
		12044	D. molecule
species	`C` (substrate)	0.01	A. uM
		1e-8	B. mole/liter
		1.0e-20	C. mole
		6.022e+3	D. molecule
species	`X` (enzyme)	0.01	A. uM
		1e-8	B. mole/liter
		1.0e-20	C. mole
		6.022e+3	D. molecule

Reaction 4 Cdc2 Kinase Activation

R4		Value	Units
reaction	`Mplus -> M`	----	----
reaction rate	`(V1*Mplus)/(K1 + Mplus)`	----	A. uM/minute
		----	B. mole/(liter*second)
		----	C. mole/second
		----	D. molecule/second
`repeatedAssignment` rule	`V1 = (VM1*C)/(Kc + C)`	----
parameter	V1 (variable by rule)	0.00	A. uM/minute B. mole/(liter*second) C. mole/second D. molecule/second
parameter	`VM1`	3.0	A. uM/minute
		5.0e-8	B. mole/(liter*second)
		5.0000e-020	C. mole/second
		30110	D. molecule/second
parameter	`Kc`	0.5	A. uM
		5.0000e-7	B. mole/liter
		5.0e-19	C. mole
		3.011e+5	D. molecule
parameter	`K1`	0.005	A. uM
		5e-9	B. mole/liter
		5e-21	C. mole
		3.011e+3	D. molecule
species	`Mplus` (inactive substrate)	0.99	A. uM
		9.9e-7	B. mole/liter
		9.9e-19	C. mole
		5.962e+5	D. molecule
species	`M` (active product)	0.01	A. uM
		1e-8	B. mole/liter
		1.0e-20	C. mole
		6.022e+3	D. molecule
species	`C`	0.01	A. uM
		1e-8	B. mole/liter
		1.0e-20	C. mole
		6.022e+3	D. molecule

Reaction 5 Cdc2 Kinase Deactivation

R5		Value	Units
reaction	`M -> M_plus`	----	----
reaction rate	`(V2*M)/(K2 + M)`	----	A. uM/minute
		----	B. (mole/liter-second)
		----	C. mole/second
		----	D. molecule/second
parameter	`V2`	1.5	A. uM/minute
		2.5000e-008	B. mole/liter-second
		2.5000e-020	C. mole/second
		15055	D. molecule/second
parameter	`K2`	0.005	A. uM
		5.0000e-009	B. mole/liter
		5.0000e-021	C. mole
		3011	D. molecule
		1.0e-20	C. mole
species	`Mplus` (inactive)	0.99	A. uM
		9.9e-7	B. mole/liter
		9.9e-19	C. mole
		5.962e+5	D. molecule
species	`M` (active)	0.01	A. uM
		1e-8	B. mole/liter
		1.0e-20	C. mole
		6.022e+3	D. molecule

Reaction 6 Protease Activation

R6		Value	Units
reaction	`Xplus -> X`	----	----
reaction rate	`(V3*Xplus)/(K3 + Xplus)`	----	A. uM/minute
		----	B. mole/(liter*second)
		----	C. mole/second
		----	D. molecule/second
`repeatedAssignment` rule	`V3 = VM3*M`	----
parameter	`V3` (variable by rule)		A. uM/minute B. mole/liter-second C. mole/second D. molecule/second
parameter	`VM3`	1.0	A. 1/minute
		0.0167	B, C, D. 1/second
parameter	`K3`	0.005	A. uM
		5e-9	B. mole/liter
		5e-21	C. mole
		3.011e+3	D. molecule
species	`Xplus` (inactive substrate)	0.99	A. uM
		9.9e-7	B. mole/liter
		9.9e-19	C. mole
		5.962e+5	D. molecule
species	`X` (active product)	0.01	A. uM
		1e-8	B. mole/liter
		1.0e-20	C. mole
		6.022e+3	D. molecule
species	`M` (enzyme)	0.01	A. uM
		1e-8	B. mole/liter
		1.0e-20	C. mole
		6.022e+3	D. molecule

Reaction 7 Protease Deactivation

R7		Value	Units
reaction	`X -> X_plus`	----	----
reaction rate	`(V4*X)/(K4 + X)`	----	A. uM/minute
		----	B. mole/(liter*second)
		----	C. mole/second
		----	D. molecule/second
parameter	`V4`	0.5	A. uM/minute
		8.3333e-009	B. mole/(liter*second)
		8.3333e-021	C. mole/second
		5.0183e+003	D. molecule/second
parameter	`K4`	0.005	A. uM
		5e-9	B. mole/liter
		5e-21	C. mole
		3011	D. molecule
species	`Xplus` (inactive)	0.99	A. uM
		9.9e-7	B. mole/liter
		9.9e-19	C. mole
		5.962e+5	D. molecule
species	`X` (active)	0.01	A. uM
		1e-8	B. mole/liter
		1.0e-20	C. mole
		6.022e+3	D. molecule

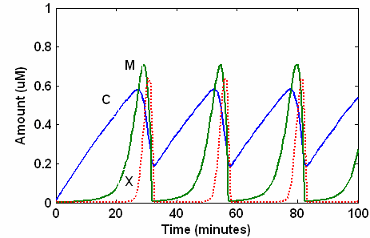
SimBiology Simulation with Reactions

This is a simulation of Goldbeter's minimal mitotic oscillator with rate and algebraic equations. Simulate with the sundials solver and plot species C, M, and X. For a description of the model, see SimBiology Model with Reactions.

References

[1] Goldbeter A. (1991), “A minimal cascade model for the mitotic oscillator involving cyclin and cdc2 kinase,” Proceedings of the National Academy of Sciences USA, 88:9107-9111.

[2] Goldbeter A., Koshland D. (1981), “An amplified sensitivity arising from covalent modification in biological systems,” Proceedings of the National Academy of Sciences USA, 78:6840-6844.

[3] Goldbeter A., Koshland D. (1984), “Ultrasensitivity in biochemical systems controlled by covalent modification,” The Journal of Biological Chemistry, 259:14441-14447.

[4] Goldbeter A., home page on the Web, http://www.ulb.ac.be/sciences/utc/GOLDBETER/agoldbet.html.

[5] Murray A.W., Kirschner M.W. (1989), “Cyclin synthesis drives the early embryonic cell cycle,” Nature, 339:275-280.