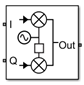
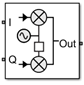
IQ Modulator
Convert baseband signal to RF signal
Libraries:
RF Blockset /
Circuit Envelope /
Systems
Description
The IQ Modulator converts a baseband signal
to RF signal and models an IQ modulator with impairments. I stands
for the in-phase component of the signal and Q stands
for the quadrature phase component of the signal. You can use the IQ
Modulator to design direct conversion transmitters.
The IQ Modulator block mask icons are dynamic and indicate the current state of the applied noise parameter. For more information, see IQ Modulator Icons.
Examples
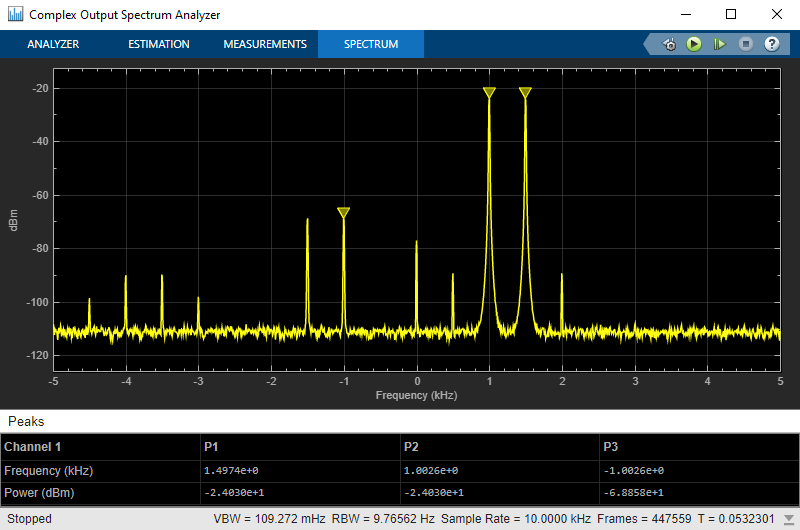
Modulate Two-Tone DC Signal Using IQ Modulator
Use the IQ Modulator block to Modulate a two-tone signal to RF level. Observe the impairments in the modulated output signal such as images due to gain imbalance, intermodulation distortion, and output third-order intercept (OIP3).
Parameters
Main
Source of conversion gain — Source parameter of conversion gain
Available power gain (default) | Open circuit voltage gain | Polynomial coefficients
Source parameter of conversion gain, specified as one of the following:
Available power gain— Relates the ratio of the power of a single sideband (SSB) of the output to the input power at theIbranch. This assumes no gain mismatch and that the input at the Q branch is Qin = - j.IinOpen circuit voltage gain— Value of the open circuit voltage gain parameter as the linear voltage gain term of the polynomial voltage-controlled voltage source (VCVS).Polynomial coefficients— Implements a nonlinear voltage gain according to the polynomial you specify.
Available power gain — Ratio of power of SSB at output to input power at I
0 dB (default) | scalar in dB or a unitless ratio
Ratio of the power of SSB at the output to input power at
I branch, specified as a scalar in dB or a
unitless ratio. For a unitless ratio, select
None.
Dependencies
To enable this parameter, set Source of conversion
gain to Available power
gain.
Open circuit voltage gain — Open circuit voltage gain
0 dB (default) | scalar in dB or a unitless ratio
Open circuit voltage of IQ modulator, specified as a scalar in dB or a
unitless ratio. For a unitless ratio, select
None.
Dependencies
To enable this parameter, set Source of conversion
gain to Open circuit voltage
gain.
Polynomial coefficients — Coefficients of polynomial specifying voltage gain
[0 1] (default) | vector
Polynomial coefficients, specified as a vector.
The order of the polynomial must be less than or equal to 9. The
coefficients must be ordered in ascending powers. If a vector has 10
coefficients,
[,
the polynomial it represents is:a0,a1,a2,
... a9]
Vout = a0 + a1Vin + a2Vin2 + ...
+ a9Vin9
a1
represents the linear gain term, and higher-order terms are modeled
according to [2].
For example, the vector
[
specifies the relation Vout = a0 + a1V1 + a2V12 + a3V13. Trailing zeros are omitted. So
a0,a1,a2,a3][
defines the same polynomial as
a0,a1,a2][.a0,a1,a2,
0]
By default, the value is [0,1], corresponding to the linear relation Vout = Vin.
Dependencies
To enable this parameter, set Source of conversion
gain to Polynomial
coefficients.
Local oscillator frequency — Local oscillator (LO) frequency
0
Hz (default) | scalar
Local oscillator (LO) frequency, specified as a scalar in Hz, kHz, MHz, or GHz.
Input impedance (Ohm) — Input impedance of IQ modulator
50 (default) | scalar
Input impedance of IQ modulator, specified as a scalar in Ohms.
Output impedance (Ohm) — Output impedance of IQ modulator
50 (default) | scalar
Output impedance of IQ modulator, specified as a scalar in Ohms.
Add Image Reject filters — Image reject (IR) filter parameters
off (default) | on
Select to add the IR filter parameter tab. Clear to remove the tab.
Add Channel Select filter — Channel select (CS) filter parameters
off (default) | on
Select to add the CS filter parameter tab. Clear to remove the tab.
Ground and hide negative terminals — Ground and hide terminals
on (default) | off
Select to internally ground and hide the negative terminals. Clear to expose the negative terminals. When the terminals are exposed, you can connect them to other parts of your model.
Edit System — Break IQ modulator block links and replace internal variables by appropriate values
button
Use this button to break IQ modulator links to the library. The internal variables are replaced by their values which are estimated using IQ modulator parameters. The IQ Modulator becomes a simple subsystem masked only to keep the icon.
Use Edit System to edit the internal variables without expanding the subsystem. Use Expand System to expand the subsystem in the Simulink™ canvas and to edit the subsystem.
Impairments
I/Q gain mismatch — Gain difference between I and Q
branches
0
dB (default) | scalar
Gain difference between I and Q
branches, specified as a scalar in dB, or a unitless ratio. Gain
mismatch is assumed to be forward-going, that is, the mismatch does not
affect leakage from LO to RF.
If the gain mismatch is specified, the value relates the ratio of power of the single-sideband
(SSB) at the Q input branch to the output
power.
I/Q phase mismatch — Phase difference between I and Q branches
0
degrees (default) | scalar in degrees or radians
Phase difference between I and Q
branches, specified as a scalar in degrees or radians. This mismatch
affects the LO to input RF leakage.
LO to RF isolation — Ratio of magnitude between LO voltage to leaked RF voltage
inf dB (default) | scalar
Ratio of magnitude between LO voltage to leaked RF voltage, specified
as a scalar in dB, or a unitless ratio. For a unitless ratio, select
None.
Noise floor (dBm/Hz) — Single-sided noise power spectral distribution
-inf (default) | scalar in dBm/Hz
Single-sided noise power spectral distribution, specified as a scalar
in dBm/Hz. This block assumes -174dBm/Hz noise input at both
I and Q branches.
Add phase noise — Add phase noise
off (default) | on
Select this parameter to add phase noise to your IQ modulator system.
Phase noise frequency offset (Hz) — Phase noise frequency offset
1 (default) | scalar | vector | matrix
Phase noise frequency offset, specified as a scalar, vector, or matrix with each element unit in Hz.
If you specify a matrix, each column corresponds to a non-DC carrier frequency of the CW source. The frequency offset values bind the envelope bandwidth of the simulation. For more information, see Configuration.
Dependencies
To enable this parameter, select Add phase noise.
Phase noise level (dBc/Hz) — Phase noise level
-Inf (default) | scalar | vector | matrix
Phase noise level, specified as a scalar, vector, or matrix with element unit in dBc/Hz.
If you specify a matrix, each column corresponds to a non-DC carrier frequency of the CW source. The frequency offset values bind the envelope bandwidth of the simulation. For more information, see Configuration.
Dependencies
To enable this parameter, select Add phase noise.
Automatically estimate impulse response duration — Automatically estimate impulse response duration
on (default) | off
Select to automatically estimate impulse response for phase noise. Clear to specify the impulse response duration using Impulse response duration.
Dependencies
To enable this parameter, select Add phase noise.
Impulse response duration — Impulse response duration
1e-10
s (default) | scalar
Impulse response duration used to simulate phase noise, specified as a scalar in s, ms, us, or ns.
Note
The phase noise profile resolution in frequency is limited by the duration of the impulse response used to simulate it. Increase this duration to improve the accuracy of the phase noise profile. A warning message appears if the phase noise frequency offset resolution is too high for a given impulse response duration. This message also specifies the minimum duration suitable for the required resolution.
Dependencies
To set this parameter, clear Automatically estimate impulse response duration.
Plot phase noise characteristics — Phase noise magnitude response
button
The block plots the phase noise characteristics based in the parameters specified on the Impairments tab and either the Envelope bandwidth parameter in the Configuration block when available or the value specified in the Phase noise frequency offset (Hz) parameter.
Dependencies
To enable this parameter, select Add phase noise.
Nonlinearity
Selecting Polynomial coefficients for
Source of conversion gain in the
Main tab removes the
Nonlinearity parameters.
Nonlinear polynomial type — Polynomial nonlinearity
Even and odd order (default) | Odd order
Polynomial nonlinearity, specified as one of the following:
Even and odd order: The IQ Modulator can produce second-order and third-order intermodulation frequencies, in addition to a linear term.Odd order: The IQ Modulator generates only "odd-order" intermodulation frequencies.The linear gain determines the linear a1 term. The block calculates the remaining terms from the values specified in IP3, 1-dB gain compression power, Output saturation power, and Gain compression at saturation. The number of constraints you specify determines the order of the model. The figure shows the graphical definition of the nonlinear IQ modulator parameters.
Intercept points convention — Intercept points convention
Output (default) | Input
Intercept points convention, specified as
Input (input-referred) or
Output (output-referred). Use this
specification for the intercept points IP2,
IP3, the 1-dB gain compression
power, and the Output saturation
power.
IP2 — Second-order intercept point
inf
dBm (default) | scalar
Second-order intercept point, specified as a scalar in dBm, W, mW, or
dBW. The default value
inf dBm
corresponds to an unspecified point.
Dependencies
To enable this parameter, set Nonlinear polynomial
type to Even and odd
order.
IP3 — Third-order intercept point
inf
dBm (default) | scalar
Third-order intercept point, specified as a scalar in dBm, W, mW, or
dBW. The default value
inf dBm
corresponds to an unspecified point.
Dependencies
To enable this parameter, set Nonlinear polynomial
type to Even and odd
order.
1-dB gain compression power — 1-dB gain compression power
inf
dBm (default) | scalar
1-dB gain compression power, specified as a scalar in dBm, W, mW, or dBW. The 1-dB gain compression point must be less than the output saturation power.
Dependencies
To enable this parameter, set Odd order
in Nonlinear polynomial type tab.
Output saturation power — Output saturation power
inf
dBm (default) | scalar
Output saturation power, specified as a scalar. The block uses this value to calculate the voltage saturation point used in the nonlinear model. In this case, the first derivative of the polynomial is zero, and the second derivative is negative.
Dependencies
To enable this parameter, set Odd order
in Nonlinear polynomial type tab.
Gain compression at saturation — Gain compression at saturation
inf
dBm (default) | scalar
Gain compression at saturation, specified as a scalar.
Dependencies
To enable this parameter, first select Odd
order in Nonlinear polynomial
type tab. Then change the default value of
Output saturation power .
IR Filter
Select Add Image Reject filters in the Main tab to see the IR Filter parameters tab.
Design method — Simulation type
Ideal (default) | Butterworth | Chebyshev
Simulation type. Simulates an ideal, Butterworth, or Chebyshev filter of the type specified in Filter type and the model specified in Implementation.
Filter type — Filter type
Lowpass (default) | Highpass | Bandpass | Bandstop
Filter. Simulates a lowpass, highpass, bandpass, or bandstop filter type of the design specified in Design method
Implementation — Implementation
LC Tee | LC Pi | Transfer function | Constant per carrier | Frequency Domain
Implementation, specified as one of the following:
LC Tee: Model an analog filter with an LC lumped Tee structure when the Design method is Butterworth or Chebyshev.LC Pi: Model an analog filter with an LC lumped Pi structure when the Design method is Butterworth or Chebyshev.Transfer Function: Model an analog filter using two-port S-parameters when the Design method is Butterworth or Chebyshev.Constant per carrier: Model a filter with either full transmission or full reflection set as constant throughout the entire envelope band around each carrier. The Design method is specified as ideal.Filter Domain: Model a filter using convolution with an impulse response. The Design method is specified as ideal. The impulse response is computed independently for each carrier frequency to capture the ideal filtering response. When a transition between full transmission and full reflection of the ideal filter occurs within the envelope band around a carrier, the frequency-domain implementation captures this transition correctly up to a frequency resolution specified in Impulse response duration.Note
Due to causality, a delay of half the impulse response duration is included for both reflected and transmitted signals. This delay impairs the filter performance when the Source and Load resistances differ from the values specified in filter parameters.
By default, the Implementation is
Constant per carrier for an ideal filter
and LC Tee for Butterworth or
Chebyshev.
Passband edge frequency — Passband edge frequency
2 GHz (default) | scalar
Passband edge frequency, specified as a scalar in Hz, kHz, MHZ, or GHz.
Dependencies
To enable this parameter, set Design method
to Ideal and Filter
type to Lowpass or
Highpass.
Implement using filter order — Implement using filter order
on (default) | off
Select this parameter to implement the filter order manually.
Dependencies
To enable this parameter, set Design method
to Butterworth or
Chebyshev.
Filter order — Filter order
3 (default) | scalar
Filter order, specified as a scalar. For a Filter
type of Lowpass or
Highpass, the filter order is the number
of lumped storage elements. For a Filter type of
Bandpass of
Bandstop, the number of lumped storage
elements is twice the filter order.
Note
For even order Chebyshev filters, the resistance ratio for Tee network implementation and for Pi network implementation.
where:
Rp is the passband ripple in dB.
Dependencies
To enable this parameter, select Implement using filter order.
Passband frequency — Passband frequency for lowpass and highpass filters
scalar
Passband frequency for lowpass and highpass filters, specified as a
scalar in Hz, kHz, MHz, or GHz. The default value is 1
GHz for Lowpass filters and
2 GHz for Highpass
filters.
Dependencies
To enable this parameter, set Design method
to Butterworth or
Chebyshev and Filter
type to Lowpass or
Highpass.
Passband frequencies — Passband frequencies for bandpass filters
[2 3] GHz (default) | 2-tuple vector
Passband frequencies for bandpass filters, specified as a 2-tuple vector in Hz, kHz, MHz, or GHz. This option is not available for bandstop filters.
Dependencies
To enable this parameter, set Design method
to Butterworth or
Chebyshev and Filter
type to Bandpass.
Passband attenuation (dB) — Passband attenuation
10*log10(2) (default) | scalar
Passband attenuation, specified as a scalar in dB. For bandpass filters, this value is applied equally to both edges of the passband.
Dependencies
To enable this parameter, set Design method
to Butterworth or
Chebyshev.
Stopband frequencies — Stopband frequencies for bandstop filters
[2.1 2.9] GHz (default) | 2-tuple vector
Stopband frequencies for bandstop filters, specified as a 2-tuple vector in Hz, kHz, MHz, or GHz. This option is not available for bandpass filters.
Dependencies
To enable this parameter, set Design method
to Butterworth or
Chebyshev and Filter
type to Bandstop.
Stopband edge frequencies — Stopband edge frequencies for ideal bandstop filters
[2.1 2.9] GHz (default) | 2-tuple vector
Stopband edge frequencies for bandstop filters, specified as a 2-tuple vector in Hz, kHz, MHz, or GHz. This option is not available for ideal bandpass filters.
Dependencies
To enable this parameter, set Design method
to Ideal and Filter
type to Bandstop.
Stopband attenuation (dB) — Stopband attenuation
40 (default) | scalar
Stopband attenuation, specified as a scalar in dB. For bandstop filters, this value is applied equally to both edges of the stopband.
Dependencies
To enable this parameter, set Design method
to Butterworth or
Chebyshev and Filter
type to Bandstop.
Source impedance (Ohm) — Input source resistance
50 (default) | scalar
Input source resistance, specified as a scalar in Ohms.
Dependencies
To enable this parameter, set Design method
to Butterworth or
Chebyshev.
Load impedance (Ohm) — Output load resistance
50 (default) | scalar
Output load resistance, specified as a scalar in Ohms.
Dependencies
To enable this parameter, set Design method
to Butterworth or
Chebyshev.
Automatically estimate impulse response duration — Automatically estimate impulse response duration
on (default) | off
Select to automatically estimate impulse response for phase noise. Clear to manually specify the impulse response duration using Impulse response duration.
Dependencies
To enable this parameter, set Design method
to Ideal and
Implementation to Frequency
domain.
Impulse response duration — Impulse response duration
1e-10
s (default) | scalar
Impulse response duration used to simulate phase noise, specified as a scalar in s, ms, us, or ns. You cannot specify impulse response if the amplifier is nonlinear.
Note
The phase noise profile resolution in frequency is limited by the duration of the impulse response used to simulate it. Increase this duration to improve the accuracy of the phase noise profile. A warning message appears if the phase noise frequency offset resolution is too high for a given impulse response duration. This message also specifies the minimum duration suitable for the required resolution
Dependencies
To enable this parameter, clear Automatically estimate impulse response duration.
Export — Save filter design to a file
button
Use this button to save filter design to a file. Valid file types are
.mat and .txt.
Dependencies
To enable this parameter, set Design method
to Butterworth or
Chebyshev.
CS Filter
Select Add Channel Select filter in the Main tab to see the CS Filter parameters.
Design method — Simulation type
Ideal (default) | Butterworth | Chebyshev
Simulation type. Simulates an ideal, Butterworth, or Chebyshev filter of the type specified in Filter type and the model specified in Implementation.
Filter type — Filter type
Lowpass (default) | Highpass | Bandpass | Bandstop
Filter. Simulates a lowpass, highpass, bandpass, or bandstop filter type of the design specified in Design method.
Implementation — Implementation
LC Tee | LC Pi | Transfer function | Constant per carrier | Frequency Domain
Implementation, specified as one of the following:
LC Tee: Model an analog filter with an LC lumped Tee structure when the Design method is Butterworth or Chebyshev.LC Pi: Model an analog filter with an LC lumped Pi structure when the Design method is Butterworth or Chebyshev.Transfer Function: Model an analog filter using two-port S-parameters when the Design method is Butterworth or Chebyshev.Constant per carrier: Model a filter with either full transmission or full reflection set as constant throughout the entire envelope band around each carrier. The Design method is specified as ideal.Filter Domain: Model a filter using convolution with an impulse response. The Design method is specified as ideal. The impulse response is computed independently for each carrier frequency to capture the ideal filtering response. When a transition between full transmission and full reflection of the ideal filter occurs within the envelope band around a carrier, the frequency-domain implementation captures this transition correctly up to a frequency resolution specified in Impulse response duration.Note
Due to causality, a delay of half the impulse response duration is included for both reflected and transmitted signals. This delay impairs the filter performance when the Source and Load resistances differ from the values specified in filter parameters.
By default, the Implementation is
Constant per carrier for an ideal filter
and LC Tee for Butterworth or
Chebyshev.
Passband edge frequency — Passband edge frequency
2 GHz (default) | scalar
Passband edge frequency, specified as a scalar in Hz, kHz, MHz, or GHz.
Dependencies
To enable this parameter, set Design method
to Ideal.
Implement using filter order — Implement using filter order
on (default) | off
Select this parameter to implement the filter order manually.
Dependencies
To enable this parameter, set Design method
to Butterworth or
Chebyshev.
Filter order — Filter order
3 (default) | scalar
Filter order, specified as a scalar. This order is the number of
lumped storage elements in lowpass or
highpass. In bandpass or
bandstop, the number of lumped storage elements
are twice the value.
Note
For even order Chebyshev filters, the resistance ratio for Tee network implementation and for Pi network implementation.
where:
Rp is the passband ripple in dB.
Dependencies
To enable this parameter, select Implement using filter order.
Passband frequency — Passband frequency for lowpass and highpass filters
scalar
Passband frequency for lowpass and highpass filters, specified as a
scalar in Hz, kHz, MHz, or GHz. By default, the passband frequency is
1 GHz for Lowpass
filters and 2 GHz for
Highpass filters.
Dependencies
To enable this parameter, set Design method
to Butterworth or
Chebyshev and Filter
type to Lowpass or
Highpass.
Passband frequencies — Passband frequencies for bandpass filters
[2 3] GHz (default) | 2-tuple vector
Passband frequencies for bandpass filters, specified as a 2-tuple vector in Hz, kHz, MHz, or GHz. This option is not available for bandstop filters.
Dependencies
To enable this parameter, set Design method
to Butterworth or
Chebyshev and Filter
type to Bandpass.
Passband attenuation (dB) — Passband attenuation
10*log10(2) (default) | scalar
Passband attenuation, specified as a scalar in dB. For bandpass filters, this value is applied equally to both edges of the passband.
Dependencies
To enable this parameter, set Design method
to Butterworth or
Chebyshev.
Stopband frequencies — Stopband frequencies for bandstop filters
[2.1 2.9] GHz (default) | 2-tuple vector
Stopband frequencies for bandstop filters, specified as a 2-tuple vector in Hz, kHz, MHz, or GHz. This option is not available for bandpass filters.
Dependencies
To enable this parameter, set Design method
to Butterworth or
Chebyshev and Filter
type to Bandstop.
Stopband edge frequencies — Stopband edge frequencies for ideal bandstop filters
[2.1 2.9] GHz (default) | 2-tuple vector
Stopband edge frequencies for bandstop filters, specified as a 2-tuple vector in Hz, kHz, MHz, or GHz. This option is not available for ideal bandpass filters.
Dependencies
To enable this parameter, set Design method
to Ideal and Filter
type to Bandstop.
Stopband attenuation (dB) — Stopband attenuation
40 (default) | scalar
Stopband attenuation, specified as a scalar in dB. For bandstop filters, this value is applied equally to both edges of the stopband.
Dependencies
To enable this parameter, set Design method
to Butterworth or
Chebyshev and Filter
type to Bandstop.
Source impedance (Ohm) — Input source resistance
50 (default) | scalar
Input source resistance, specified as a scalar in Ohms.
Dependencies
To enable this parameter, set Design method
to Butterworth or
Chebyshev.
Load impedance (Ohm) — Output load resistance
50 (default) | scalar
Output load resistance, specified as a scalar in Ohms.
Dependencies
To enable this parameter, set Design method
to Butterworth or
Chebyshev.
Automatically estimate impulse response duration — Automatically estimate impulse response duration
on (default) | off
Select to automatically estimate impulse response for phase noise. Clear to specify the impulse response duration using Impulse response duration.
Dependencies
To enable this parameter, set Design method
to Ideal and
Implementation to Frequency
domain.
Impulse response duration — Impulse response duration
1e-10s (default) | scalar
Impulse response duration used to simulate phase noise, specified as a scalar in s, ms, us, or ns. You cannot specify impulse response if the amplifier is nonlinear.
Note
The phase noise profile resolution in frequency is limited by the duration of the impulse response used to simulate it. Increase this duration to improve the accuracy of the phase noise profile. A warning message appears if the phase noise frequency offset resolution is too high for a given impulse response duration. This message also specifies the minimum duration suitable for the required resolution
Dependencies
To set this parameter, clear Automatically estimate impulse response duration.
Export — Save filter design to a file
button
Use this button to save filter design to a file. Valid file types are
.mat and .txt.
Dependencies
To enable this parameter, set Design method
to Butterworth or
Chebyshev.
Algorithms
IQ Modulator Icons
This table shows you how the icons on this block will vary based on how you set the Noise figure (dB) and Add LO phase noise parameters on the block.
| Noise figure (dB) | Add LO phase noise: off | Add LO phase noise: on |
|---|---|---|
0 |
|
|
10 |
|
|
References
[1] Razavi, Behzad. RF Microelectronics. Upper Saddle River, NJ: Prentice Hall, 2011.
[2] Grob, Siegfried and Lindner, Jurgen, “Polynomial Model Derivation of Nonlinear Amplifiers”, Department of Information Technology, University of Ulm, Germany.
Version History
Introduced in R2017aSee Also
You can also select a web site from the following list
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)
Asia Pacific
- Australia (English)
- India (English)
- New Zealand (English)
- 中国
- 日本Japanese (日本語)
- 한국Korean (한국어)