Main Content

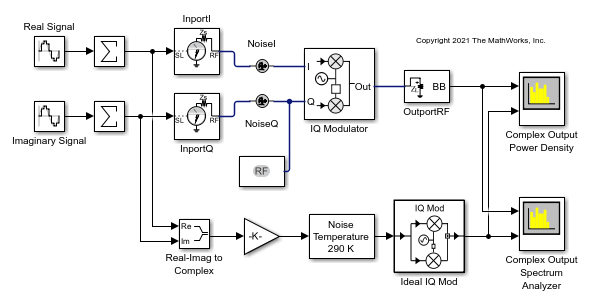
Modulate Quadrature Baseband Signals Using IQ Modulators

This example uses:

Open Script

This example shows how to modulate quadrature baseband signals using two different RF Blockset™ blocks. You can use either an idealized baseband Mixer block or a circuit envelope IQ Modulator block in your model to modulate quadrature baseband signals to the RF level. Observe the impairments in the modulated output signal due to gain imbalance, third-order intercepts (OIP3) and system noise in the complex output power density and output power spectrum analyzers.

The input in-phase and quadrature baseband signals are each composed of two tones at 10 MHz and 15 MHz and the power of each baseband signal is -30 dBm. When using a circuit envelope IQ Modulator block to modulate the signal, you must use Inport and Outport blocks to set the input and output carrier frequencies. The explicit noise sources in the model set the noise floor in each signal branch.

Set Parameters

For idealized baseband Mixer block

  • Mixer type — IQ Modulator

  • Sideband — Upper

  • Gain (dB) — 10 dB

  • IIP3 (dBm) — 10 dBm

  • Select Include mixer noise

  • I/Q gain imbalance (dB) — 0.1 dB

  • Noise figure (dB) — 3.9752 dB

The Noise figure (dB) is calculated using this equation

(Room Temperature Noise Floor,Boltmanns x 290) – dB_to_dBm – CE_IQModulator_Noise_Floor – IDBB_Mixer_Conversion_Gain

= 10 x log10(1.3806452e-23 x 290) – 30 – 160 – 10 = 3.9752 dB

For circuit envelope IQ Modulator block

  • Available power gain — 10 dB

  • Local oscillator frequency — 2 GHz

  • IP3 — 10 dBm

  • I/Q gain mismatch — 0.1 dB

  • LO to RF Isolation — inf dB

  • Noise Floor — –160 dBm/Hz

  • Select Add Image Reject filter

Since the input signals are baseband signals, the inport blocks Carrier frequencies are set to 0 and the input signal power is interpreted correctly. For the Ideal Baseband Mixer branch, a Gain block with Gain equal to 1/(sqrt(2)) is required. If the input signals are complex baseband, then the gain is set to 1/2.

Run the model and observe the output of the Spectrum Analyzer blocks.

Analyze Complex Output Power Density Plot

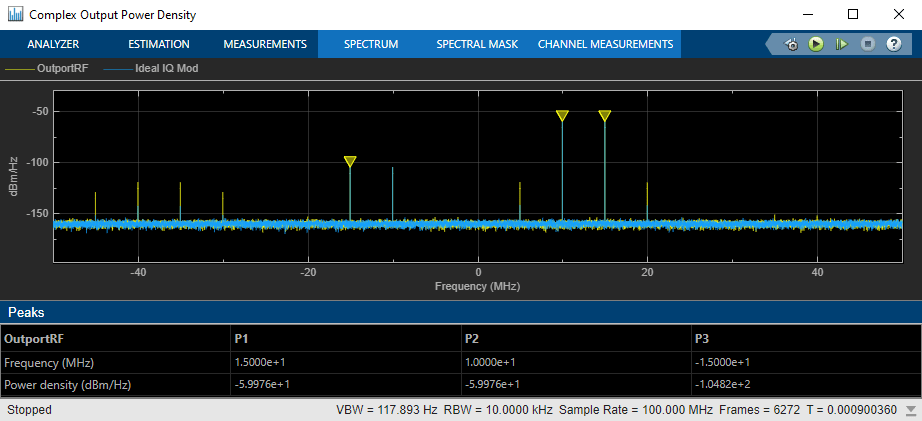
In the complex output power density spectrum analyzer plot, the noise floor of the signal is at – 160 dBm/Hz for the two output signals OutportRF and Ideal IQ Mod.

Analyze Complex Output Spectrum Analyzer Plot

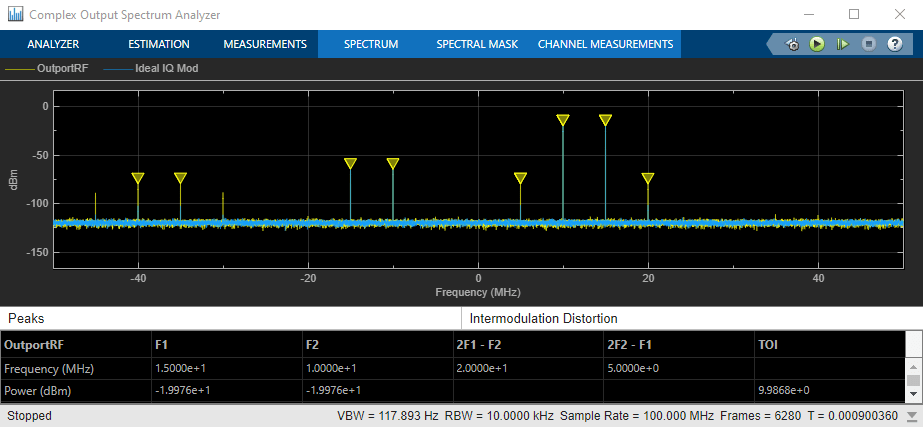
In the complex output spectrum analyzer plot, the modulated signal along with other signal tones produced by the impairments are shown. The output power levels at 10 MHz and 15 MHz are – 20 dBm. The level of the other output tones are correct for circuit envelope, since it is a multi-tone simulator. Any differences between the modulated signals, 10 MHz and 15 MHz, result from different model implementations for the I/Q gain and phase mismatch. You can calculate the output power level using this formula:

Output_Power_Level(dBm) = Input_Power_Level(dBm) + Gain(dBm) = – 30 + 10 = – 20

See Also

Related Topics