Main Content

Examine Effect of Diffusion Coefficient and Volume Fraction on Battery Terminal Voltage

Since R2024b
Open Live Script

This example shows how the diffusion coefficient and the volume fraction of the electrode active material of a Battery Single Particle block affect the battery terminal voltage.

For a single-particle-model battery, the diffusion coefficient quantifies the rate at which lithium ions diffuse inside the active particles of the electrode material and is essential for the charge and discharge cycles of the battery. You can use the diffusion coefficient to calculate the concentration gradient and flux of lithium ions in the electrode particles during their insertion or removal. To describe this ion movement, the single-particle model usually assumes spherical particles and applies Fick's laws of diffusion.

The active material volume fraction represents the proportion of the electrode volume that the active material occupies. The terminal voltage of a battery is inversely related to the rate of the active material depletion due to the changes in the battery capacity and in the rate at which the state of charge (SOC) decreases during the discharge.

This figure shows the change in the lithium-ion normalized concentration inside the anode and the cathode, and the terminal voltage of the battery during a discharging cycle:

Media1.gif (2).gif

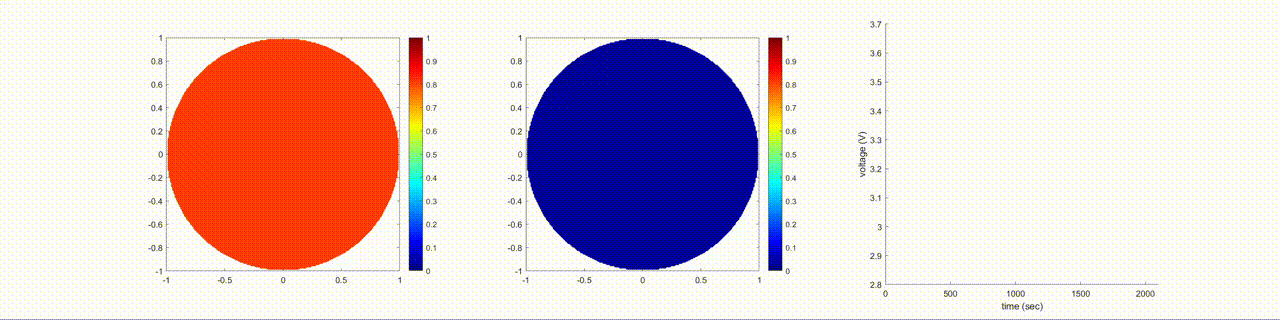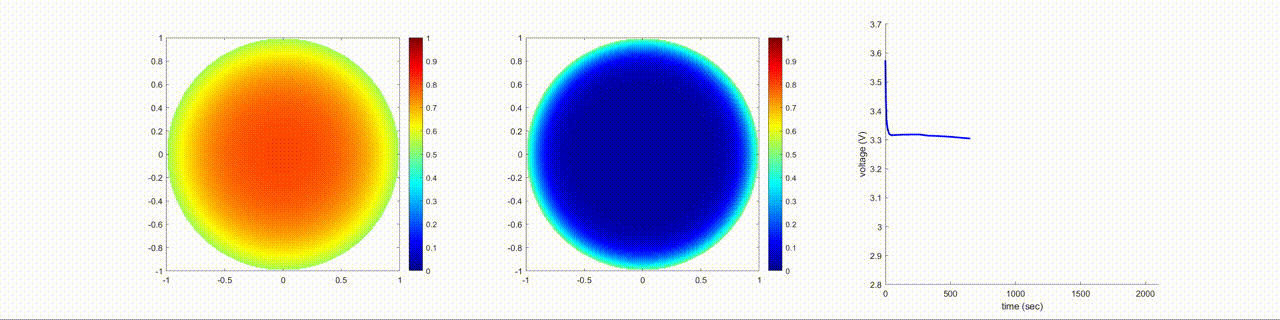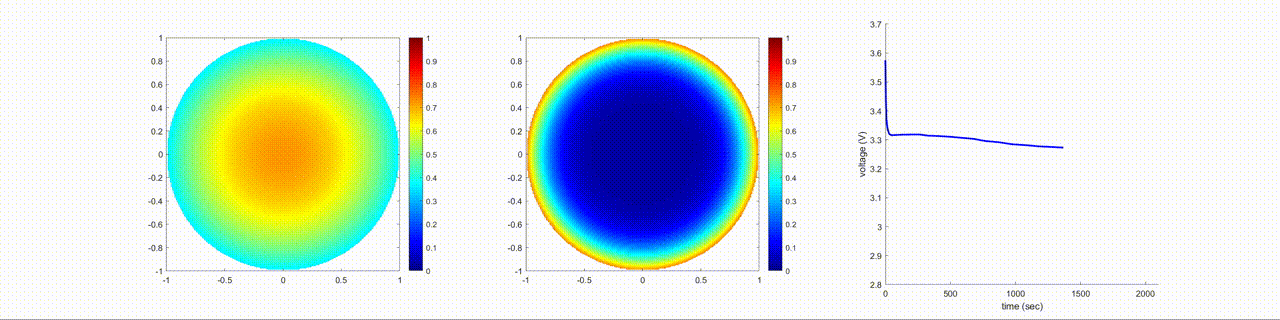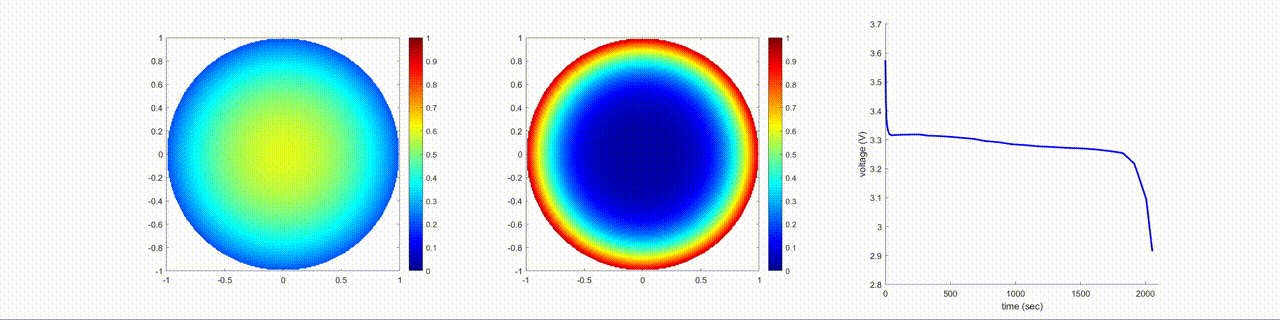
Examine Effect of Cathode Diffusion Coefficient

The diffusion coefficient of the active material in the cathode affects these characteristics of a battery during the charging and discharging cycles:

  • Speed of lithium ions — With a higher diffusion coefficient, the lithium ions in the cathode material move faster and the battery operates at higher charge and discharge rates. Conversely, a lower diffusion coefficient limits the speed of the lithium ions, reducing the battery ability to rapidly charge and discharge.

  • Distribution of lithium ions — A uniform distribution of the lithium ions in the cathode particles enhances the capacity of the battery. If the diffusion coefficient is too low, the lithium ions do not penetrate deeply enough inside the cathode particles, especially during fast charging or discharging cycles. This poor penetration reduces the effective capacity of the battery.

  • Voltage efficiency — Poor diffusion leads to larger concentration gradients of the lithium ions inside the cathode particles, resulting in higher overpotentials during charging and discharging. The energy efficiency of the battery decreases.

  • Thermal behavior — Faster diffusion rates maintain more uniform reaction rates throughout the electrode and contribute to the thermal management. However, if a slow diffusion results in a high concentration gradient, the battery can experience localized heating and stress inside the particles.

Open Model

Open the BatterySingleParticleDiffusion model. In this example, a Controlled Current Source block discharges the Battery Single Particle block with a current of -0.5A for 500 seconds. After 500 seconds, the current immediately becomes 0 A and the battery undergoes a period of relaxation. 

open_system("BatterySingleParticleDiffusion");

Set the state of charge of the battery to 0.72. This value means that the battery is not fully charged at the start of the simulation.

set_param('BatterySingleParticleDiffusion/Battery Single Particle','stateOfCharge','0.72');

Modify Cathode Diffusion Coefficient and Simulate Model

Specify two values for the diffusion coefficient of the active material in the cathode. The second diffusion coefficient is 10 times greater than the first diffusion coefficient.

FirstDiffusionCoefficient = 5e-20;
SecondDiffusionCoefficient = 10*FirstDiffusionCoefficient;

Set the Diffusion coefficient of cathode active material parameter of the battery to the value of the first diffusion coefficient and simulate the model.

set_param('BatterySingleParticleDiffusion/Battery Single Particle','ActiveMaterialDiffusionCoefficientCathode','FirstDiffusionCoefficient')
out = sim('BatterySingleParticleDiffusion.slx');
FirstDiffusionCoefficientVoltage = out.logsout{1}.Values;

Set the Diffusion coefficient of cathode active material parameter of the battery to the value of the second diffusion coefficient and simulate the model.

set_param('BatterySingleParticleDiffusion/Battery Single Particle','ActiveMaterialDiffusionCoefficientCathode','SecondDiffusionCoefficient')
out = sim('BatterySingleParticleDiffusion.slx');
SecondDiffusionCoefficientVoltage = out.logsout{1}.Values;

Plot and Compare Results

Plot and compare the results of the two simulations with two different diffusion coefficients.

figure(Name='Diffusion Coefficient for ExamineEffectOfCoefficientsOnTerminalVoltageExample',Position=[0 0 1600 500]);
subplot(1,2,1), plot(FirstDiffusionCoefficientVoltage); hold on; 
subplot(1,2,2), plot(FirstDiffusionCoefficientVoltage); hold on; 
subplot(1,2,1), plot(SecondDiffusionCoefficientVoltage); 
subplot(1,2,2), plot(SecondDiffusionCoefficientVoltage); 
legend_str{1} = num2str(FirstDiffusionCoefficient); 
legend_str{2} = num2str(SecondDiffusionCoefficient);
legend(legend_str);
subplot(1,2,1), xlim([0 1500]); title('Diffusion Coefficient Effect')
subplot(1,2,2), xlim([1000 7200]); title('Diffusion Coefficient Effect')

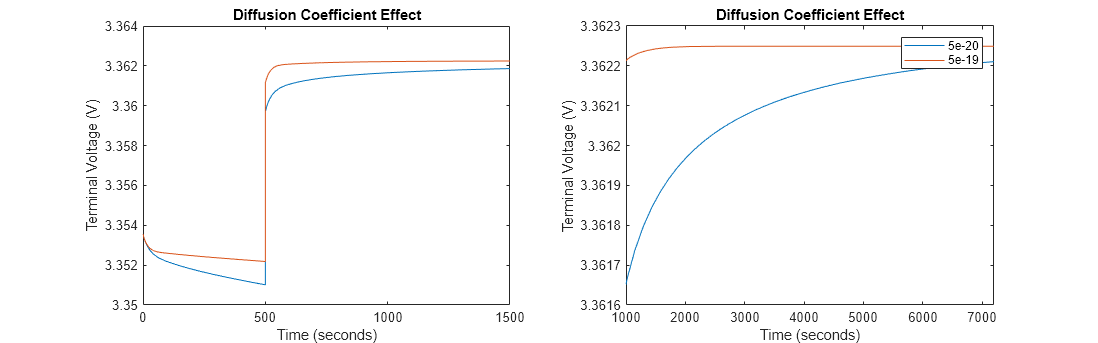
Figure Diffusion Coefficient for ExamineEffectOfCoefficientsOnTerminalVoltageExample contains 2 axes objects. Axes object 1 with title Diffusion Coefficient Effect, xlabel Time (seconds), ylabel Terminal Voltage (V) contains 2 objects of type line. Axes object 2 with title Diffusion Coefficient Effect, xlabel Time (seconds), ylabel Terminal Voltage (V) contains 2 objects of type line. These objects represent 5e-20, 5e-19.

During the discharging step, in the battery with a diffusion coefficient equal to 5e-20 m^2/s, the lithium ions move slowly inside the cathode material. This slower movement leads to a significant concentration gradient of lithium ions, resulting in a higher concentration overpotential. The significant concentration overpotential due to the lower diffusion coefficient results in a more substantial drop in terminal voltage during discharge. In the battery with a diffusion coefficient that is 10 times higher, the lithium ions move quickly inside the cathode material. This faster movement reduces the concentration gradient, resulting in a lower concentration overpotential. The drop in terminal voltage during the discharge is less severe compared to the scenario with the lower diffusion coefficient. The battery then operates more efficiently, with a higher terminal voltage under the same discharge conditions.

After the discharge step, in the relaxation period, the concentration gradients dissipate as the system moves towards the equilibrium. In the battery with a diffusion coefficient equal to 5e-20 m^2/s, the terminal voltage recovers towards the open-circuit voltage (OCV) as the concentration overpotential decreases. However, due to the lower diffusion coefficient, this recovery is slow as concentration gradients take longer to equalize across the cathode material. In the battery with a diffusion coefficient that is 10 times higher, the equalization of the lithium-ion concentration inside the cathode material is faster and the terminal voltage recovers more rapidly towards the OCV compared to the scenario with the lower diffusion coefficient.

Examine Effect of Active Material Volume Fraction

The active material volume fraction represents the proportion of the electrode volume that the active material occupies. The active material is the material that participates in the electrochemical reactions. Changing this fraction affects the capacity of the battery and the rate at which it delivers current.

Open Model

Open the BatterySingleParticleVolumeFraction model. In this example, a Controlled Current Source block discharges the Battery Single Particle block with a constant current of -1.16 A for 700 seconds.

open_system("BatterySingleParticleVolumeFraction");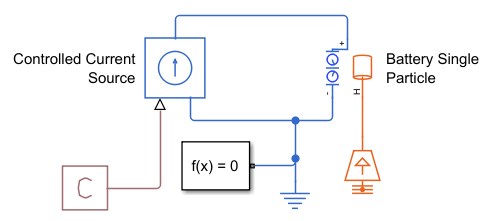

Set the state of charge of the battery to 1. This value means that the battery is fully charged at the start of the simulation.

set_param('BatterySingleParticleVolumeFraction/Battery Single Particle','stateOfCharge','1');

Modify Cathode Diffusion Coefficient and Compare Results

Specify the values of the active material volume fraction for the anode and cathode. These values are the baseline against which you compare the effect of modifying the active material volume fraction of the battery. 

VolumeFractionAnode = 0.58;
VolumeFractionCathode = 0.374;

Run four simulations and plot the results. In each simulation, you are setting the Volume fraction of anode active material and Volume fraction of cathode active material parameters of the Battery Single Particle block to the baseline values you specified before multiplied by a scaling factor of 0.9, 1, 1.1, and 1.2, respectively.

j = 1;
figure(Name='Volume Fraction for ExamineEffectOfCoefficientsOnTerminalVoltageExample');
for ScalingFactor = 0.9:0.1:1.2
    set_param('BatterySingleParticleVolumeFraction/Battery Single Particle','ActiveMaterialVolumeFractionAnode','VolumeFractionAnode*ScalingFactor');
    set_param('BatterySingleParticleVolumeFraction/Battery Single Particle','ActiveMaterialVolumeFractionCathode','VolumeFractionCathode*ScalingFactor');
    out = sim('BatterySingleParticleVolumeFraction.slx');
    TerminalVoltage = out.logsout{1}.Values;
    plot(TerminalVoltage); hold on;
    legend_str{j} = strcat(num2str(ScalingFactor),' x baseline');
    j = j + 1;
end
legend(legend_str);
title('Active Material Volume Fraction Effect')

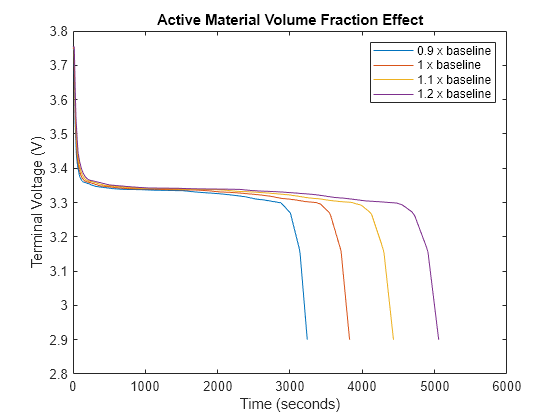
Figure Volume Fraction for ExamineEffectOfCoefficientsOnTerminalVoltageExample contains an axes object. The axes object with title Active Material Volume Fraction Effect, xlabel Time (seconds), ylabel Terminal Voltage (V) contains 4 objects of type line. These objects represent 0.9 x baseline, 1 x baseline, 1.1 x baseline, 1.2 x baseline.

The terminal voltage is inversely related to the rate of the active material depletion due to the changes in the battery capacity and in the rate at which the SOC decreases during the discharge. Lower volume fractions lead to faster voltage drops, while higher volume fractions lead to slower voltage drops, resulting in higher terminal voltages at the same discharge time points.

Examine the four different scenarios more closely:

  • Scaling factor equal to 0.9 — The volume fraction of the active material inside the battery is 10% lower than the baseline value. The effective capacity of the battery reduces because there is less active material available for the electrochemical reactions. The terminal voltage drops more quickly compared to the baseline scenario because the reduced volume fraction of the active material leads to faster depletion of the available charge. The battery reaches a lower SOC value faster, resulting in a lower terminal voltage at the same time points.

  • Scaling factor equal to 1 — This is the baseline value of the volume fraction of the active material. The terminal voltage follows the expected discharge curve based on the constant current and volume fraction.

  • Scaling factor equal to 1.1 — The volume fraction of the active material inside the battery is 10% higher than the baseline value. The effective capacity of the battery increases because there is more active material available for the electrochemical reactions. The terminal voltage decreases more slowly compared to the baseline scenario. The increased active material volume fraction means that the battery sustains the discharge current for a longer period before reaching the same SOC value. Therefore, at the same time points, the terminal voltage is higher than in the baseline scenario.

  • Scaling factor equal to 1.2 — The volume fraction of the active material inside the battery is 20% higher than the baseline value. The effective capacity further increases. The terminal voltage decreases even more slowly compared to the other scenarios. The battery delivers the discharge current for an even longer period before reaching the same SOC value. Therefore, at the same time points, the terminal voltage is higher than in all other scenarios.

See Also