Battery Single Particle

Battery model with single-particle approach

Since R2024a

Libraries:
Simscape / Battery / Cells

Description

The Battery Single Particle block represents a battery by using a single-particle model. This implementation considers the ohmic and mass transport overpotentials in both the liquid electrolyte and solid electrode phases. Additionally, it considers the reaction kinetics and the current collector resistance.

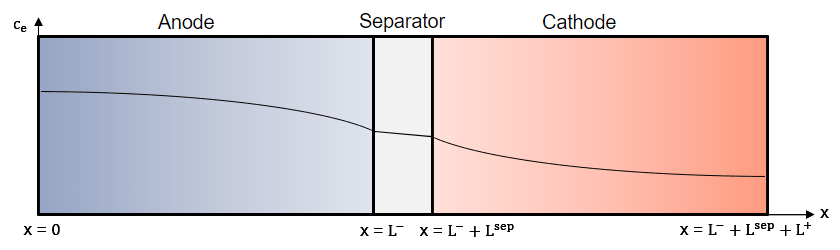
The battery comprises two electrodes, the anode and cathode, and a porous separator between the electrodes. In this block, the anode refers to the negative electrode during discharge and the cathode refers to the positive electrode during discharge. The block models the ohmic overpotentials of the electrodes and electrolyte, as well as the concentration across the cell cross section from the anode current collector to the cathode current collector, in a one-dimensional framework.

This figure illustrates a representative concentration in the electrolyte during discharge. The model comprises the anode (x=[0 … L^-]), the separator (x=[L^- … L^-+L^sep]) and the cathode (x=[L^-+L^sep… L^-+L^sep+L⁺]).

Representative concentration in the electrolyte during discharge. The model comprises the anode, the separator, and the cathode.

The block calculates the concentration in the electrodes in representative spherical particles across the radial dimension r. This figure shows the concentration gradient in the representative particles during a continuous discharge of the battery:

Concentration gradient in the representative particles during a continuous discharge of the battery.

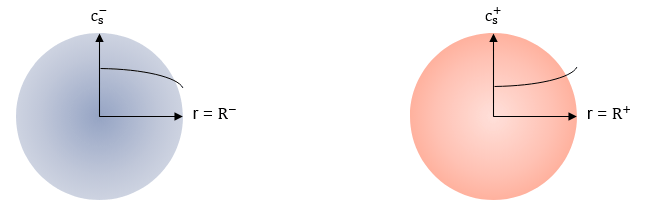
Species Conservation in Solid Phase

When the block is in solid phase, the single-particle approach models the positive and negative electrodes as a single representative spherical particle.

Note

The superscripts in these equations refer to the respective electrodes. A + superscript refers to the cathode. A - superscript refers to the anode. A sep superscript refers to the separator. A ± superscript means that the equation applies to both anode and cathode. For example, c⁺_s is the solid-phase concentration of the cathode and c^-_s is the solid-phase concentration of the anode.

This equation uses Fick's law to describe the concentration, c, of the cation in the negative or positive electrode. The block uses the radial coordinates only to calculate the concentration in the electrodes. The diffusion in the spherical particle drives the mass transfer,

$\frac{\partial c_{s}^{\pm}}{\partial t} (r, t) = \frac{\partial}{\partial r} [D_{s}^{\pm} \frac{\partial c_{s}^{\pm}}{\partial r} (r, t)],$

where:

c_s is the solid-phase concentration.
D_s is the diffusion coefficient in solid phase.
r is the radius.
t is the time.

At the center of the particle, the concentration gradient is equal to 0:

$D_{s}^{\pm} \frac{\partial c_{s}^{\pm}}{\partial r} (0, t) = 0.$

This equation calculates the ion concentration gradient at the surface of the particle:

$D_{s}^{\pm} \frac{\partial c_{s}^{\pm}}{\partial r} (R_{s}^{\pm}, t) = \mp \frac{J_{s}^{\pm}}{a_{s}^{\pm} F} .$

In this equation, F is Faraday's constant, and J is the molar flux,

$J^{\pm} (t) = \frac{I (t)}{A L^{\pm}},$

where:

I is the current applied to the cell.
A is the total area of the current collector.
L is the length of the respective electrode.

Additionally, a is the active surface area per electrode unit volume,

$a^{\pm} = \frac{3 ε^{\pm}}{R^{\pm}},$

where:

ε is the active material fraction of the electrode.
R is the total radius of the active particle.

To solve the differential equation, the Battery Single Particle block discretizes the particle with the radius R into n shells. Each shell has a radial distance equal to $δ r = \frac{R}{n}$ from the adjacent spheres.

For the ith sphere, this equation calculates the rate of change of concentration, δc/δt:

${\dot{c}}_{s_{i}} = \frac{D_{s}}{δ r^{2}} {(\frac{i - 1}{i}) c_{s_{i - 1}} - 2 c_{s_{i}} + (\frac{i + 1}{i}) c_{s_{i + 1}}} .$

For the innermost shell in the particle, the block implements this boundary condition:

${\dot{c}}_{1} = \frac{2 D_{s}}{δ r^{2}} {c_{s_{2}} - c_{s_{1}}} .$

To implement the boundary condition at the surface of the particle, the block adds an additional node around the surface. The block does not calculate the concentration of this node because it does not physically exist. The block uses this node to calculate the boundary condition between the outermost shell in the particle and the non-existent shell around it by using the Neumann boundary condition. This equation describes the discretized result at the surface of the particle:

${\dot{c}}_{s_{e n d}} = \frac{2 D_{s}}{δ r^{2}} {c_{s_{e n d - 1}} - c_{s_{e n d}}} - 2 \frac{n + 1}{n} \frac{J}{F A δ r} .$

Mass Transport Overpotential in Solid Phase

When the block is in solid phase, the open-circuit potential depends on the concentration. To calculate the mass transport overpotential at the electrodes, the Battery Single Particle block subtracts the open-circuit potential of the average relative concentration in the particle from the open-circuit potential of the average relative concentration at the surface,

$η^{\pm}_{diffusion, s} = {ocp}^{\pm} (c_{s, surface, relative}^{\pm}) - {ocp}^{\pm} ({\bar{c}}_{s, relative}^{\pm}),$

where:

η_diffusion_,s is the solid-phase mass transport overpotential.
ocp(c_s,_{surface,relative}) is the open-circuit potential for the concentration at the surface of the particle.
ocp(c_s_relative) is the open-circuit potential for the average concentration of the particle.

The block uses the same equation to calculate the mass transport overpotential for both the anode and the cathode.

Ohmic Overpotential in Solid Phase

To calculate the ohmic overpotential when the block is in the solid phase, the Battery Single Particle block linearly approximates the current across the electrodes and the current at the current collector to a value equal to the electric current applied to the cell. The current at the interface between the current separator and the electrode is zero. This equation defines the ohmic overpotential in the solid phase,

$η^{\pm}_{o h m i c, s} = \frac{I_{b a t t}}{2 A} * \frac{L^{\pm}}{κ^{\pm}},$

where:

η_ohmic,s is the solid-phase ohmic overpotential.
I_batt/A is the cell cross section.
L is the length of the respective electrode and depends on the thickness of the anode or cathode.
κ is the conductivity. The conductivity depends on the temperature of the cell. κ is equal to the Anode conductivity parameter when the block calculates the ohmic overpotential of the anode and is equal to the Cathode conductivity parameter when the block calculates the ohmic overpotential of the cathode.

The block uses the same equation to calculate the ohmic overpotential in solid phase for both the anode and the cathode.

Species Conservation in Liquid Phase

When the block is in liquid phase, this equation describes the concentration in the electrolyte at both electrodes and at the separator. To calculate the concentration across the separator, the block considers the diffusive flow induced by concentration gradient,

$\frac{\partial c_{ε}^{\pm}}{\partial t} (x, t) = \frac{\partial}{\partial x} [D_{ε} \frac{\partial c_{ε}^{\pm}}{\partial x} (x, t)],$

where:

c_ε is the concentration in the electrolyte.
D_ε is the diffusion coefficient in liquid phase.
x is the location in the thickness of the battery, from the anode current collector to the cathode current collector.
t is the time.

At the positive and negative electrodes, the block considers both the diffusive flow and the cation flux from the solid electrode into the electrolyte,

$\in_{ε}^{\pm} \frac{\partial c_{ε}^{\pm}}{\partial t} (x, t) = \frac{\partial}{\partial x} [D_{ε}^{e f f} \frac{\partial c_{ε}^{\pm}}{\partial x} (x, t) \pm \frac{(1 - t_{+}^{0}) J}{F}],$

where:

∈ is the volume fraction of the electrolyte.
D^eff_ε is the diffusion coefficient in the liquid phase that considers the porosity of the material. The diffusivity of the liquid electrolyte depends on the properties of the surrounding solid electrode material. The electrode comprises multiple components, such as the active material and the filler, that form a characteristic porous material.
J is the molar flux.
t⁺ is the transference number of the cation.
F is Faraday's constant.

Because the electrolyte is a continuous fluid, the cation concentration at the border between the negative and positive electrodes and the separator must be equal. For the concentration in the electrolyte at the anode-separator and cathode-separator interfaces, the block must define the boundary conditions between the three sections of the battery. The block represents both electrodes and the separator as cuboids.

This block considers the electrolyte as a continuous medium across the electrodes and the separator. Because the concentrations on both sides of the interface must be equal, a continuity boundary condition exists for the interface between the electrodes and the separator.

This equation describes the continuity boundary condition for the concentration at the interface between the anode and the separator,

$c_{ε}^{-} (L^{-}, t) = c_{ε}^{s e p} (L^{-}, t),$

where:

$c_{ε}^{-} (L^{-}, t)$ is the concentration in the anode at the border between the anode and the separator.
$c_{ε}^{s e p} (L^{-}, t)$ is the concentration in the separator at the border between the anode and the separator.

This equation describes the continuity boundary condition for the concentration at the interface between separator and cathode,

$c_{ε}^{s e p} (L^{-} + L^{s e p}, t) = c_{ε}^{+} (L^{-} + L^{s e p}, t),$

where:

$c_{ε}^{s e p} (L^{-} + L^{s e p}, t)$ is the concentration in the separator at the border between the separator and the cathode.
$c_{ε}^{+} (L^{-} + L^{s e p}, t)$ is the concentration in the cathode at the border between the separator and the cathode.

The block also applies a flux boundary condition to the interfaces between the electrodes and the separator. The flux at both sides of the interface must be equal,

$\begin{array}{l} D_{e f f}^{-} \frac{\partial c_{ε}^{-}}{\partial x} (L^{-}, t) = D_{e f f}^{s e p} \frac{\partial c_{ε}^{s e p}}{\partial x} (L^{-}, t) \\ D_{e f f}^{+} \frac{\partial c_{ε}^{+}}{\partial x} (L^{-} + L^{s e p}, t) = D_{e f f}^{s e p} \frac{\partial c_{ε}^{s e p}}{\partial x} (L^{-} + L^{s e p}, t) \end{array}$

where:

$D_{e f f}^{-}$ is the diffusion coefficient of the anode.
$D_{e f f}^{+}$ is the diffusion coefficient of the cathode.
$D_{e f f}^{s e p}$ is the diffusion coefficient of the separator.
$\frac{\partial c_{ε}^{-}}{\partial x} (L^{-}, t)$ is the concentration gradient of the anode at the border between the anode and the separator.
$\frac{\partial c_{ε}^{s e p}}{\partial x} (L^{-}, t)$ is the concentration gradient of the separator at the border between the anode and the separator.
$\frac{\partial c_{ε}^{+}}{\partial x} (L^{-} + L^{s e p}, t)$ is the concentration gradient of the cathode at the border between the cathode and the separator.
$\frac{\partial c_{ε}^{s e p}}{\partial x} (L^{-} + L^{s e p}, t)$ is the concentration gradient of the separator at the border between the cathode and the separator.

This equation specifies the concentration at the boundaries between the electrodes and the current collectors. The flux is proportional to the flux at the current collector, which is equal to zero because the block does not store any ions there. Hence the resulting flux at the interface is zero,

$\frac{\partial c_{ε}^{-}}{\partial x} (0, t) = \frac{\partial c_{ε}^{+}}{\partial x} (L^{-} + L^{s e p} + L^{+}, t) = 0,$

where:

$\frac{\partial c_{ε}^{-}}{\partial x} (0, t)$ is the concentration gradient in the anode at the border between the anode and the leftmost current collector.
$\frac{\partial c_{ε}^{+}}{\partial x} (L^{-} + L^{s e p} + L^{+}, t)$ is the concentration gradient in the cathode at the border between the cathode and the rightmost current collector.

Similar to the solid phase, the block solves the differential equation by dividing the electrolyte into n sections of equal size. This equation expresses the concentration in the ith section with a distance δx between sections, and is valid for all [1,M_s-1] sections:

$\frac{\partial c_{ε}}{\partial t} (x, t) = D_{ε, e f f}^{\pm} \frac{c_{i + 1} + c_{i - 1} - 2 c_{i}}{\partial x^{2}} + \frac{(1 - t_{+}^{0}) J}{F} .$

The block discretizes the separator using the equation:

$\frac{\partial c_{ε}}{\partial t} (x, t) = D_{ε, e f f}^{s e p} \frac{c_{i + 1} + c_{i - 1} - 2 c_{i}}{δ x^{2}} .$

To calculate the concentrations at the interfaces between the electrodes and the separator, the block applies all the boundary conditions. For example, for the interface between the anode and the separator, the block applies the equation:

$c_{ε, i = 1}^{s e p} = \frac{ε_{ε}^{-}}{ε_{ε}^{s e p}} \frac{c_{ε, i = 0} - c_{ε, i = - 1}^{s e p}}{\partial x} \partial x - c_{ε, i = 0} .$

Mass Transport Overpotential in Liquid Phase

When the block is in the liquid phase, it uses the concentrations at the interfaces between the current collector and the anode and at the interfaces between the cathode and the current collector to calculate the mass transport overpotential in the electrolyte using the equation,

$η_{d i f f u s i o n, ε} = \frac{2 R T}{F} (1 - t_{ε}^{0}) \ln \frac{c_{ε} (L^{-} + L^{s e p} + L^{+}, t)}{c_{ε} (0, t)},$

where:

R is the universal gas constant.
T is the temperature.
F is Faraday's constant.

Ohmic Overpotential in Liquid Phase

When the block is in the liquid phase, it calculates the ohmic overpotential by linearly approximating the ionic current in each section of the battery. For the electrodes, the ionic current at the interface to the current collector is zero. At the interface to the separator, the ionic current is equal to the electric current of the battery, I_batt. Across the separator, the block approximates the ionic current as constant and equal to the electric current applied to the battery. The block calculates the ohmic overpotential using the equation

$η_{o h m i c, ε} = - \frac{I_{b a t t}}{2 A} * (\frac{L^{+}}{κ_{e f f}^{+}} + 2 \frac{L^{s e p}}{κ_{e f f}^{s e p}} + \frac{L^{-}}{κ_{e f f}^{-}}),$

where κ_eff is the effective conductivity that the block calculates by using the Bruggeman coefficient. For more information about effective parameters, see the Effective Electrolyte Properties section.

Charge Transfer Overpotential

To model the charge transfer overpotential, this block uses the Butler-Volmer equation. The Butler-Volmer equation describes the relationship between the current density, j, and the overpotential, η, which is the difference between the actual electrode potential and the thermodynamic equilibrium potential. The Butler-Volmer equation is

$J^{\pm} (t) = j_{0, k} (t) [\exp (\frac{α n_{ε} F}{R T} η^{\pm} (t)) - \exp (- \frac{(1 - α) n_{ε} F}{R T} η^{\pm} (t))],$

where:

α is the charge transfer coefficient for the oxidation and reduction.
j₀ is the exchange current density.

Solving the equation for the electrode overpotential results in these equations:

$\begin{array}{l} η_{kinetic,s} = \frac{R T}{α F} \ln (ξ^{\pm} + \sqrt{{(ξ^{\pm})}^{2} + 1}) \\ ξ^{\pm} = \frac{j^{\pm}}{2 a^{\pm} i_{0}^{\pm}} \end{array}$

i^±₀ is the exchange current density in the anode and in the cathode and is equal to

$i_{0}^{\pm} = k^{\pm} {[{\bar{c}}_{ε}^{\pm} (c_{s, \max}^{\pm} - c_{s, s u r f}^{\pm}) c_{s, s u r f}^{\pm}]}^{α},$

where:

k is the charge transfer rate constant and is equal to the value of the Charge transfer rate constant for Anode parameter for the anode and to the value of the Charge transfer rate constant for Cathode parameter for the cathode.
${\bar{c}}_{ε}^{\pm}$ is the average electrolyte concentration.
c_s,max is the maximum electrode concentration.
c_s,surf is the electrode surface concentration.

To calculate the kinetic overpotential of the complete cell, the block subtracts the kinetic overpotential at the anode from the kinetic overpotential at the cathode:

$η_{kinetic,s} = η^{+}_{kinetic,s} - η^{-}_{kinetic,s} .$

Current Collector Resistance

This block models the current collector resistance as a single resistance. You can set the current collector resistance by specifying the Current collector resistance parameter.

Cell Voltage

To model the cell voltage, this block considers the potentials at the surfaces of each electrode, the overpotentials, and the voltage loss due to the current collector resistance by using the equation

$V (t) = {ocp}^{+} (c_{surface,relative}^{+}) - {ocp}^{-} (c_{surface,relative}^{-}) + η_{diffusion, ε} + η_{o h m i c, ε} + η_{kinetic, s} + η_{o h m i c}^{-} + η_{o h m i c}^{+} + I_{batt} R_{CurrentCollector},$

where:

ocp⁺(c⁺_{surface,relative}) is the open-circuit potential for the concentration at the surface of the cathode particle.
ocp^-(c^-_{surface,relative}) is the open-circuit potential for the concentration at the surface of the anode particle.
η_diffusion,ε is the mass transport overpotential in the electrolyte.
η_ohmic,ε is the ohmic overpotential in the electrolyte.
η_kinetic,s is the charge transfer overpotential in the electrodes.
η^-_ohmic is the ohmic overpotential in the anode.
η⁺_ohmic is the ohmic overpotential in the cathode.
I_batt is the battery current.
R_{CurrentCollector} is the resistance of the current collector.

You can parameterize the open-circuit potential as table data by using the relative concentration as the breakpoints by specifying the Anode open-circuit potential, Cathode open-circuit potential, and Normalized stoichiometry breakpoints parameters.

To calculate the relative concentration, the block considers the maximum concentration and the maximum and minimum stoichiometry of each electrode. The Anode maximum ion concentration and the Cathode maximum ion concentration parameters represent the theoretically possible maximum concentration of each electrode. To obtain the achievable maximum and minimum concentrations, the block multiplies the values of these parameters with the value of the Anode maximum stoichiometry, Anode minimum stoichiometry, Cathode maximum stoichiometry, and Cathode minimum stoichiometry parameters, respectively. Then, the block calculates the relative concentration by using the equation

$c_{s,relative} = \frac{\frac{c_{s}}{c_{s, \max}} - Ν_{\min}}{Ν_{\max} - Ν_{\min}},$

where:

c_s,_max is the maximum concentration.
N_max is the maximum stoichiometry.
N_min is the minimum stoichiometry.

Effective Electrolyte Properties

Set the values of these parameters based on the microstructure of the porous electrodes you want to model:

Diffusion coefficient of electrolyte — Set this parameter to the value of the diffusion coefficient of the electrolyte that influences the mass transport in the electrolyte.
Electrolyte conductivity — Set this parameter to the value of the conductivity of the electrolyte.

To model this dependency, this block uses the Bruggeman correlation,

${Parameter}_{effective} = {Parameter}_{block} * φ_{ε}^{α},$

where:

φ_ε is the volume fraction of the electrolyte. This value is equal to the value of the Volume fraction of electrolyte in anode, Volume fraction of electrolyte in separator, and Volume fraction of electrolyte in cathode parameters, accordingly.
α is the Bruggeman exponent. This value is equal to the value of the Anode Bruggeman exponent, Separator Bruggeman exponent, and Cathode Bruggeman exponent parameters, accordingly.

Thermal

The block considers the temperature constant across the cell. These block parameters depend on the temperature of the cell:

Diffusion coefficient of anode active material and Diffusion coefficient of cathode active material— These parameters are the diffusion coefficients of electrodes that influence the mass transport in the electrodes.
Diffusion coefficient of electrolyte — This parameter is the diffusion coefficient of electrolyte that influences the mass transport in the electrolyte.
Electrolyte conductivity — This parameter is the conductivity of the electrolyte.
Anode conductivity and Cathode conductivity — These parameters are the conductivity of the electrodes.
Charge transfer rate constant for Anode and Charge transfer rate constant for Cathode — These parameters are the charge transfer rate constants of the electrodes.

To calculate the temperature-adjusted values of these parameters, the block uses the Arrhenius equation,

${Parameter}_{T-adjusted} = {Parameter}_{block} * e^{\frac{E_{a}}{R} (\frac{1}{T_{r e f}} - \frac{1}{T})},$

where:

Parameter_block is the value of the temperature-dependent parameters.
E_a is the activation energy and is equal to the value of the activation energy parameters in the Thermal settings.
T_ref is the value of the Arrhenius reference temperature parameter.
T is the battery temperature.

Heat Generation of Battery

This block models the battery as a lumped thermal mass. The single-particle model calculates the irreversible heat generation that the overpotentials cause in the battery by using this equation:

$Q = I_{b a t t} (η_{diffusion, ε} + η_{o h m i c, ε} + η_{o h m i c, s}^{-} + η_{o h m i c, s}^{+} + I_{batt} R_{CurrentCollector} + η_{kinetic, s} + η^{+}_{diffusion} + η^{-}_{diffusion}) .$

Public Variables

You can use the Probe block to access these variables in the Battery Single Particle block. The units are the default values.

anodeModel.averageStoichiometry — Average stoichiometry in the anode.
anodeModel.massTransportOverpotential — Mass transport overpotential, in volts.
anodeModel.normalizedAverageStoichiometry — Average stoichiometry normalized to the minimum and maximum values.
anodeModel.normalizedSurfaceStoichiometry — Surface stoichiometry normalized to the minimum and maximum values.
anodeModel.ohmicOverpotential — Ohmic overpotential of the anode, in volts.
anodeModel.shellConcentration — Concentration of the modeled shells, in mol/m^3. The number of shells is equal to the value of the Anode Shell Count parameter.
anodeModel.shellStoichiometry — Stoichiometry of the modeled shells. The number of shells is equal to the Anode Shell Count parameter.
anodeModel.surfaceConcentration — Concentration at the surface of the particle, in mol/m^3.
anodeModel.surfacePotential — Potential at the surface of the particle, in volts.
anodeModel.temperatureAdjustedConductivity — Conductivity adjusted to the battery temperature, in S/m.
anodeModel.temperatureAdjustedDiffusionCoefficient — Diffusion coefficient adjusted to the battery temperature, in m^2/s.
averageElectrolyteConcentration — Average concentration in the particle, in mol/m^3.
batteryCurrent — Total current measured through the battery terminals, in amperes.
batteryTemperature — Battery average temperature that the block uses for the table lookup of resistances and open-circuit voltage. If you set the Thermal model parameter to Constant temperature, the batteryTemperature variable is equal to the specified temperature value. If you set the Thermal model parameter to Lumped thermal mass, the batteryTemperature variable is a differential state that varies during the simulation.
batteryVoltage — Battery terminal voltage, or the voltage difference between the positive and the negative terminals, in volts.
cathodeModel.averageStoichiometry — Average stoichiometry in the cathode.
cathodeModel.massTransportOverpotential — Mass transport overpotential, in volts.
cathodeModel.normalizedAverageStoichiometry — Average stoichiometry normalized to the minimum and maximum values.
cathodeModel.normalizedSurfaceStoichiometry — Surface stoichiometry normalized to the minimum and maximum values.
cathodeModel.ohmicOverpotential — Ohmic overpotential of the cathode, in volts.
cathodeModel.shellConcentration — Concentration of the modeled shells, in mol/m^3. The number of shells is equal to the value of the Anode Shell Count parameter.
cathodeModel.shellStoichiometry — Stoichiometry of the modeled shells. The number of shells is equal to the Anode Shell Count parameter.
cathodeModel.surfaceConcentration — Concentration at the surface of the particle, in mol/m^3.
cathodeModel.surfacePotential — Potential at the surface of the particle, in volts.
cathodeModel.temperatureAdjustedConductivity — Conductivity adjusted to the battery temperature, in S/m.
cathodeModel.temperatureAdjustedDiffusionCoefficient — Diffusion coefficient adjusted to the battery temperature, in m^2/s.
electrolyteModel.averageConcentration — Average concentration in the electrolyte across the whole cell, in mol/m^3.
electrolyteModel.averageConcentrationAnode — Average concentration in the electrolyte inside the anode, in mol/m^3.
electrolyteModel.averageConcentrationCathode — Average concentration in the electrolyte inside the cathode, in mol/m^3.
electrolyteModel.averageConcentrationSeparator — Average concentration in the electrolyte inside the separator, in mol/m^3.
electrolyteModel.concentrationAnode — Concentration of the modeled layers of the electrolyte in the anode, in mol/m^3. The number of elements is equal to the Electrolyte layer count of anode parameter.
electrolyteModel.concentrationCathode — Concentration of the modeled layers of the electrolyte in the cathode, in mol/m^3. The number of elements is equal to the Electrolyte layer count of cathode parameter.
electrolyteModel.concentrationSeparator — Concentration of the modeled layers of the electrolyte in the separator, in mol/m^3. The number of elements is equal to the Electrolyte layer count of electrolyte parameter.
electrolyteModel.currentDensityAnode — Current density in the anode, in A/m^3.
electrolyteModel.currentDensityCathode — Current density in the cathode, in A/m^3.
electrolyteModel.diffusionCoefficientAnode — Temperature-adjusted effective diffusion coefficient of the electrolyte in the anode, in m^s/s.
electrolyteModel.diffusionCoefficientCathode — Temperature-adjusted effective diffusion coefficient of the electrolyte in the cathode, in m^s/s.
electrolyteModel.diffusionCoefficientSeparator — Temperature-adjusted effective diffusion coefficient of the electrolyte in the separator, in m^s/s.
electrolyteModel.conductivityAnode — Temperature-adjusted effective conductivity of the electrolyte in the anode, in S/m.
electrolyteModel.conductivityCathode — Temperature-adjusted effective conductivity of the electrolyte in the cathode, in S/m.
electrolyteModel.effectiveConductivitySeparator — Temperature-adjusted effective conductivity of the electrolyte in the separator, in S/m.
electrolyteModel.massTransportOverpotential — Mass transport overpotential of the electrolyte, in volts.
electrolyteModel.ohmicOverpotential — Ohmic overpotential of the electrolyte, in volts.
electrolyteModel.temperatureAdjustedConductivity — Temperature-adjusted conductivity of the electrolyte, in S/m.
electrolyteModel.temperatureAdjustedDiffusionCoefficient — Temperature adjusted diffusion coefficient of the electrolyte, in m^s/s.
heatGenerationRate — Total battery heat generation rate, in watts. The block calculates the heat generation rate by adding the resistive losses and the reversible heating contributions.
power_dissipated — Resistive heat generation rate or dissipated power, in watts.
reactionKineticsModel.chargeTransferOverpotential — Charge transfer overpotential of the battery, in volts.
reactionKineticsModel.exchangeCurrentDensityAnode — Exchange current density in the anode, in C/(m^2*s).
reactionKineticsModel.exchangeCurrentDensityCathode — Exchange current density in the cathode, in C/(m^2*s).
reactionKineticsModel.temperatureAdjustedChargeTransferRateAnode — Temperature-adjusted charge transfer rate constant for the anode, in m^(5/2)/(mol^(1/2) * s).
reactionKineticsModel.temperatureAdjustedChargeTransferRateCathode — Temperature-adjusted charge transfer rate constant for the cathode, in m^(5/2)/(mol^(1/2) * s).
stateOfCharge — Battery state of charge obtained from Coulomb counting.
thermalModel.batteryTemperature — Temperature of the battery, in K.
thermalModel.cellTemperature — Temperature output by the cell.
thermalModel.heatDissipationRate — Heat dissipation rate of the battery, in watts.
thermalModel.heatGeneration — Heat that the battery generates, in watts.
thermalModel.thermalMass — Thermal mass of the battery, in J/K.

Examples

New

Examine Effect of Diffusion Coefficient and Volume Fraction on Battery Terminal Voltage

How the diffusion coefficient and the volume fraction of the electrode active material of a Battery Single Particle block affect the battery terminal voltage.

Since R2024b
Open Live Script

Ports

Conserving

expand all

+ — Positive terminal
electrical

Electrical conserving port associated with the positive battery terminal.

- — Negative terminal
electrical

Electrical conserving port associated with the negative battery terminal.

H — Battery thermal mass
thermal

Thermal conserving port associated with the thermal mass of the battery.

Parameters

expand all

To edit block parameters interactively, use the Property Inspector. From the Simulink^® Toolstrip, on the Simulation tab, in the Prepare gallery, select Property Inspector.

Main

Extrapolation method for all tables — Method of extrapolation for tables
`Nearest` (default) | `Linear` | `Error`

Extrapolation method for the table-based parameters:

Linear — Estimate values beyond the data by creating a tangent line at the end of the known data and extending it beyond that limit.
Nearest — Extrapolate a value at a query point that is the value at the nearest sample grid point.
Error — Return an error if the value goes beyond the known data. If you select this option, the block does not use extrapolation.

Programmatic Use

To set the block parameter value programmatically, use the set_param function.

Parameter:	`ExtrapolationMethod`
Values:	`"nearest"` (default) \| `"linear"` \| `"error"`

Geometry

Anode thickness — Thickness of anode
`3.4E-5` `m` (default) | positive scalar

Thickness of the anode.

Electrolyte layer count of anode — Electrolyte layer count of anode
`10` (default) | scalar greater than 3

Electrolyte layer count of the anode.

Separator thickness — Thickness of separator
`2.5E-5m` (default) | positive scalar

Thickness of the separator.

Electrolyte layer count of separator — Electrolyte layer count of separator
`5` (default) | scalar greater than 3

Electrolyte layer count of the separator.

Cathode thickness — Thickness of cathode
`8E-5m` (default) | positive scalar

Thickness of the cathode.

Electrolyte layer count of cathode — Electrolyte layer count of cathode
`10` (default) | scalar greater than 3

Electrolyte layer count of the cathode.

Electrode plate area — Area of electrode plate
`1.8E-1m^2` (default) | positive scalar

Area of the electrode plate.

Anode particle radius — Particle radius of anode
`5E-6m` (default) | positive scalar

Particle radius of the anode.

Anode shell count — Number of shells for anode
`10` (default) | positive scalar greater than 3

Number of shells for the anode.

Cathode particle radius — Particle radius of cathode
`5E-8m` (default) | positive scalar

Particle radius of the cathode.

Cathode shell count — Number of shells for cathode
`10` (default) | positive scalar greater than 3

Number of shells for the cathode.

Electrodes Properties

Volume fraction of anode active material — Volume fraction of active material in anode
`0.58` (default) | scalar in the range (0,1)

Volume fraction of the active material in the anode.

Volume fraction of cathode active material — Volume fraction of active material in cathode
`0.374` (default) | scalar in the range (0,1)

Volume fraction of the active material in the cathode.

Anode open-circuit potential — Open-circuit potential of anode
`[.484; .335; .253; .209; .2; .181; .165; .151; .139; .131; .128; .125; .124; .124; .123; .122; .119; .117; .111; .108; .101; .098; .095; .093; .092; .088; .088; .088; .088; .087; .087; .087; .085; .082; .079; .071; .064; .049; .026]` `V` (default) | vector of positive elements

Open-circuit potential of the anode. The size of this parameter must be equal to the size of the Normalized stoichiometry breakpoints parameter.

Cathode open-circuit potential — Open-circuit potential of cathode
`[3.81; 3.608; 3.512; 3.478; 3.459; 3.453; 3.45257; 3.45214; 3.45171; 3.45128; 3.45085; 3.45042; 3.44999; 3.44956; 3.44913; 3.4487; 3.44827; 3.44784; 3.44741; 3.44698; 3.44655; 3.44612; 3.44569; 3.44526; 3.44483; 3.4444; 3.44397; 3.44354; 3.44311; 3.44268; 3.44225; 3.44182; 3.44139; 3.44096; 3.44053; 3.44; 3.412; 3.304; 2.968]` `V` (default) | vector of positive elements

Open-circuit potential of the cathode. The size of this parameter must be equal to the size of the Normalized stoichiometry breakpoints parameter.

Normalized stoichiometry breakpoints — Stoichiometry breakpoints for open-circuit potential of electrode
`linspace(0.025, 0.975, 39)` (default) | vector of elements in the range [0,1]

Stoichiometry breakpoints for the open-circuit potential of the electrode. The size of this parameter must be equal to the size of the Anode open-circuit potential and Cathode open-circuit potential parameters.

Note

A value of 0 means that the stoichiometry of the particle is equal to the minimum stoichiometry of the electrode, as you specify in the Anode minimum stoichiometry and Cathode minimum stoichiometry parameters. A value of 1 means that the stoichiometry of the particle is equal to the maximum stoichiometry of the electrode, as you specify in the Anode maximum stoichiometry and Cathode maximum stoichiometry parameters.

Overall, the block calculates the values of the normalized stoichiometry by using this equation:

$NormalizedSurfaceStoichiometry = \frac{ElectrodeStoichiometry(end) - MinimumStoichiometry}{MaximumStoichiometry - MinimumStoichiometry} .$

Anode maximum ion concentration — Maximum ion concentration in anode
`30555` `mol/m^3` (default) | positive scalar

Maximum ion concentration in the anode.

Anode maximum stoichiometry — Maximum stoichiometry in anode
`0.811` (default) | positive scalar

Maximum stoichiometry in the anode. The value of this parameter must be greater than the value of the Anode minimum stoichiometry parameter.

Anode minimum stoichiometry — Minimum stoichiometry in anode
`0.0132` (default) | positive scalar

Minimum stoichiometry in the anode. The value of this parameter must be less than the value of the Anode maximum stoichiometry parameter.

Cathode maximum ion concentration — Maximum ion concentration in cathode
`22806` `mol/m^3` (default) | positive scalar

Maximum ion concentration in the cathode.

Cathode maximum stoichiometry — Maximum stoichiometry in cathode
`0.74` (default) | positive scalar

Maximum stoichiometry in the cathode. The value of this parameter must be greater than the value of the Cathode minimum stoichiometry parameter.

Cathode minimum stoichiometry — Minimum stoichiometry in cathode
`0.035` (default) | positive scalar

Minimum stoichiometry in the cathode. The value of this parameter must be less than the value of the Cathode maximum stoichiometry parameter.

Diffusion coefficient of anode active material — Diffusion coefficient of active material in anode
`3E-15` `m^2/s` (default) | positive scalar

Diffusion coefficient of the active material in the anode.

Diffusion coefficient of cathode active material — Diffusion coefficient of active material in cathode
`5.9E-20` `m^2/s` (default) | positive scalar

Diffusion coefficient of the active material in the cathode.

Anode conductivity — Conductivity of anode
`100` `S/m` (default) | positive scalar

Conductivity of the anode.

Cathode conductivity — Conductivity of cathode
`0.5` `S/m` (default) | positive scalar

Conductivity of the cathode.

Current collector resistance — Resistance of current collector
`0` `Ohm` (default) | nonnegative scalar

Resistance of the current collector.

Electrolyte Properties

Volume fraction of electrolyte in anode — Fraction of volume of electrolyte in anode
`0.3874` (default) | scalar in the range (0,1)

Fraction of the volume of the electrolyte in the anode.

Volume fraction of electrolyte in separator — Fraction of volume of electrolyte in separator
`0.45` (default) | scalar in the range (0,1)

Fraction of the volume of the electrolyte in the separator.

Volume fraction of electrolyte in cathode — Fraction of volume of electrolyte in cathode
`0.5725` (default) | scalar in the range (0,1)

Fraction of the volume of the electrolyte in the cathode.

Electrolyte conductivity — Conductivity of electrolyte
`0.29` `S/m` (default) | positive scalar

Conductivity of the electrolyte.

Anode Bruggeman exponent — Bruggeman exponent of anode
`1.5` (default) | scalar greater than or equal to 1

Bruggeman exponent of the anode.

Separator Bruggeman exponent — Bruggeman exponent of separator
`1.5` (default) | scalar greater than or equal to 1

Bruggeman exponent of the separator.

Cathode Bruggeman exponent — Bruggeman exponent of cathode
`1.5` (default) | scalar greater than or equal to 1

Bruggeman exponent of the cathode.

Transference number — Fraction of total electric current that ion carries in electrolyte
`0.363` (default) | scalar in the range [0,1]

Fraction of the total electric current that an ion carries in an electrolyte.

Diffusion coefficient of electrolyte — Diffusion coefficient of electrolyte
`2E-10` `m^2/s` (default) | positive scalar

Diffusion coefficient of the electrolyte that the block uses inside the Fick's Law equation.

Reaction Kinetics

Charge transfer rate constant for Anode — Rate constant of charge transfer for anode
`8.8E-11` `m^(5/2)/(mol^(1/2)*s)` (default) | positive scalar

Rate constant of the charge transfer for the anode. The block uses this value in the Butler-Volmer equation to model the electrochemical kinetics at the electrode-electrolyte interface.

Charge transfer rate constant for Cathode — Rate constant of charge transfer for cathode
`2.8E-13` `m^(5/2)/(mol^(1/2)*s)` (default) | positive scalar

Rate constant of the charge transfer for the cathode. The block uses this value in the Butler-Volmer equation to model the electrochemical kinetics at the electrode-electrolyte interface.

Thermal

Battery thermal mass — Thermal mass of battery associated with thermal port
`77` `J/K` (default) | positive scalar

Thermal mass at the thermal port H. This parameter represents the energy required to raise the temperature of the thermal port by one kelvin.

Arrhenius reference temperature — Arrhenius reference temperature
`298.15` `K` (default) | positive scalar

Arrhenius reference temperature.

Activation energy for diffusion in anode active material — Activation energy for diffusion inside active material of anode
`39000` `J/mol` (default) | positive scalar

Activation energy for the diffusion inside the active material of the anode.

Activation energy for diffusion in cathode active material — Activation energy for diffusion inside active material of cathode
`35000` `J/mol` (default) | positive scalar

Activation energy for the diffusion inside the active material of the cathode.

Activation energy for diffusion in electrolyte — Activation energy for diffusion inside electrolyte
`26600` `J/mol` (default) | positive scalar

Activation energy for the diffusion inside the electrolyte.

Activation energy for conduction in anode — Activation energy for conduction inside anode
`3000` `J/mol` (default) | positive scalar

Activation energy for the conduction inside the anode.

Activation energy for conduction in cathode — Activation energy for conduction inside cathode
`3000` `J/mol` (default) | positive scalar

Activation energy for the conduction inside the cathode.

Activation energy for conduction in electrolyte — Activation energy for conduction inside electrolyte
`11000` `J/mol` (default) | positive scalar

Activation energy for the conduction inside the electrolyte.

Activation energy for charge transfer in Anode — Activation energy for charge transfer inside anode
`13000` `J/mol` (default) | positive scalar

Activation energy for the charge transfer inside the anode.

Activation energy for charge transfer in Cathode — Activation energy for charge transfer inside cathode
`20000` `J/mol` (default) | positive scalar

Activation energy for the charge transfer inside the cathode.

References

[1] Prada, E., D. D. Domenico, Y. Creff, J. Bernard, V. Sauvant-Moynot, and F. Huet. “Simplified Electrochemical and Thermal Model of LiFePO₄-Graphite Li-Ion Batteries for Fast Charge Applications.” Journal of The Electrochemical Society 159, no. 9 (August 2012): A1508–A1519. https://doi.org/10.1149/2.064209jes.

[2] Kemper, P. and D. Kum. “Extended Single Particle Model of Li-Ion Batteries Towards High Current Applications”. In 2013 IEEE Vehicle Power and Propulsion Conference (VPPC), 1–6, 2013. https://doi.org/10.1109/VPPC.2013.6671682.

[3] Weaver, T., A. Allam, and S. Onori. “A Novel Lithium-Ion Battery Pack Modeling Framework - Series-Connected Case Study.” In 2020 American Control Conference (ACC), 365–372. Denver, CO, USA: IEEE, 2020. https://doi.org/10.23919/ACC45564.2020.9147546.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced in R2024a

Battery Single Particle

Description

Species Conservation in Solid Phase

Mass Transport Overpotential in Solid Phase

Ohmic Overpotential in Solid Phase

Species Conservation in Liquid Phase

Mass Transport Overpotential in Liquid Phase

Ohmic Overpotential in Liquid Phase

Charge Transfer Overpotential

Current Collector Resistance

Cell Voltage

Effective Electrolyte Properties

Thermal

Heat Generation of Battery

Public Variables

Examples

Examine Effect of Diffusion Coefficient and Volume Fraction on Battery Terminal Voltage

Ports

Conserving

+ — Positive terminal electrical

- — Negative terminal electrical

H — Battery thermal mass thermal

Parameters

Main

Extrapolation method for all tables — Method of extrapolation for tables Nearest (default) | Linear | Error

Programmatic Use

Geometry

Anode thickness — Thickness of anode 3.4E-5 m (default) | positive scalar

Electrolyte layer count of anode — Electrolyte layer count of anode 10 (default) | scalar greater than 3

Separator thickness — Thickness of separator 2.5E-5m (default) | positive scalar

Electrolyte layer count of separator — Electrolyte layer count of separator 5 (default) | scalar greater than 3

Cathode thickness — Thickness of cathode 8E-5m (default) | positive scalar

Electrolyte layer count of cathode — Electrolyte layer count of cathode 10 (default) | scalar greater than 3

Electrode plate area — Area of electrode plate 1.8E-1m^2 (default) | positive scalar

Anode particle radius — Particle radius of anode 5E-6m (default) | positive scalar

Anode shell count — Number of shells for anode 10 (default) | positive scalar greater than 3

Cathode particle radius — Particle radius of cathode 5E-8m (default) | positive scalar

Cathode shell count — Number of shells for cathode 10 (default) | positive scalar greater than 3

Electrodes Properties

Volume fraction of anode active material — Volume fraction of active material in anode 0.58 (default) | scalar in the range (0,1)

Volume fraction of cathode active material — Volume fraction of active material in cathode 0.374 (default) | scalar in the range (0,1)

Normalized stoichiometry breakpoints — Stoichiometry breakpoints for open-circuit potential of electrode linspace(0.025, 0.975, 39) (default) | vector of elements in the range [0,1]

Anode maximum ion concentration — Maximum ion concentration in anode 30555 mol/m^3 (default) | positive scalar

Anode maximum stoichiometry — Maximum stoichiometry in anode 0.811 (default) | positive scalar

Anode minimum stoichiometry — Minimum stoichiometry in anode 0.0132 (default) | positive scalar

Cathode maximum ion concentration — Maximum ion concentration in cathode 22806 mol/m^3 (default) | positive scalar

Cathode maximum stoichiometry — Maximum stoichiometry in cathode 0.74 (default) | positive scalar

Cathode minimum stoichiometry — Minimum stoichiometry in cathode 0.035 (default) | positive scalar

Diffusion coefficient of anode active material — Diffusion coefficient of active material in anode 3E-15 m^2/s (default) | positive scalar

Diffusion coefficient of cathode active material — Diffusion coefficient of active material in cathode 5.9E-20 m^2/s (default) | positive scalar

Anode conductivity — Conductivity of anode 100 S/m (default) | positive scalar

Cathode conductivity — Conductivity of cathode 0.5 S/m (default) | positive scalar

Current collector resistance — Resistance of current collector 0 Ohm (default) | nonnegative scalar

Electrolyte Properties

Volume fraction of electrolyte in anode — Fraction of volume of electrolyte in anode 0.3874 (default) | scalar in the range (0,1)

Volume fraction of electrolyte in separator — Fraction of volume of electrolyte in separator 0.45 (default) | scalar in the range (0,1)

Volume fraction of electrolyte in cathode — Fraction of volume of electrolyte in cathode 0.5725 (default) | scalar in the range (0,1)

Electrolyte conductivity — Conductivity of electrolyte 0.29 S/m (default) | positive scalar

Anode Bruggeman exponent — Bruggeman exponent of anode 1.5 (default) | scalar greater than or equal to 1

Separator Bruggeman exponent — Bruggeman exponent of separator 1.5 (default) | scalar greater than or equal to 1

Cathode Bruggeman exponent — Bruggeman exponent of cathode 1.5 (default) | scalar greater than or equal to 1

Transference number — Fraction of total electric current that ion carries in electrolyte 0.363 (default) | scalar in the range [0,1]

Diffusion coefficient of electrolyte — Diffusion coefficient of electrolyte 2E-10 m^2/s (default) | positive scalar

Reaction Kinetics

Charge transfer rate constant for Anode — Rate constant of charge transfer for anode 8.8E-11 m^(5/2)/(mol^(1/2)*s) (default) | positive scalar

Charge transfer rate constant for Cathode — Rate constant of charge transfer for cathode 2.8E-13 m^(5/2)/(mol^(1/2)*s) (default) | positive scalar

Thermal

Battery thermal mass — Thermal mass of battery associated with thermal port 77 J/K (default) | positive scalar

Arrhenius reference temperature — Arrhenius reference temperature 298.15 K (default) | positive scalar

Activation energy for diffusion in anode active material — Activation energy for diffusion inside active material of anode 39000 J/mol (default) | positive scalar

Activation energy for diffusion in cathode active material — Activation energy for diffusion inside active material of cathode 35000 J/mol (default) | positive scalar

Activation energy for diffusion in electrolyte — Activation energy for diffusion inside electrolyte 26600 J/mol (default) | positive scalar

Activation energy for conduction in anode — Activation energy for conduction inside anode 3000 J/mol (default) | positive scalar

Activation energy for conduction in cathode — Activation energy for conduction inside cathode 3000 J/mol (default) | positive scalar

Activation energy for conduction in electrolyte — Activation energy for conduction inside electrolyte 11000 J/mol (default) | positive scalar

Activation energy for charge transfer in Anode — Activation energy for charge transfer inside anode 13000 J/mol (default) | positive scalar

Activation energy for charge transfer in Cathode — Activation energy for charge transfer inside cathode 20000 J/mol (default) | positive scalar

References

Extended Capabilities

C/C++ Code Generation Generate C and C++ code using Simulink® Coder™.

+ — Positive terminal
electrical

- — Negative terminal
electrical

H — Battery thermal mass
thermal

Extrapolation method for all tables — Method of extrapolation for tables
`Nearest` (default) | `Linear` | `Error`

Anode thickness — Thickness of anode
`3.4E-5` `m` (default) | positive scalar

Electrolyte layer count of anode — Electrolyte layer count of anode
`10` (default) | scalar greater than 3

Separator thickness — Thickness of separator
`2.5E-5m` (default) | positive scalar

Electrolyte layer count of separator — Electrolyte layer count of separator
`5` (default) | scalar greater than 3

Cathode thickness — Thickness of cathode
`8E-5m` (default) | positive scalar

Electrolyte layer count of cathode — Electrolyte layer count of cathode
`10` (default) | scalar greater than 3

Electrode plate area — Area of electrode plate
`1.8E-1m^2` (default) | positive scalar

Anode particle radius — Particle radius of anode
`5E-6m` (default) | positive scalar

Anode shell count — Number of shells for anode
`10` (default) | positive scalar greater than 3

Cathode particle radius — Particle radius of cathode
`5E-8m` (default) | positive scalar

Cathode shell count — Number of shells for cathode
`10` (default) | positive scalar greater than 3

Volume fraction of anode active material — Volume fraction of active material in anode
`0.58` (default) | scalar in the range (0,1)

Volume fraction of cathode active material — Volume fraction of active material in cathode
`0.374` (default) | scalar in the range (0,1)

Normalized stoichiometry breakpoints — Stoichiometry breakpoints for open-circuit potential of electrode
`linspace(0.025, 0.975, 39)` (default) | vector of elements in the range [0,1]

Anode maximum ion concentration — Maximum ion concentration in anode
`30555` `mol/m^3` (default) | positive scalar

Anode maximum stoichiometry — Maximum stoichiometry in anode
`0.811` (default) | positive scalar

Anode minimum stoichiometry — Minimum stoichiometry in anode
`0.0132` (default) | positive scalar

Cathode maximum ion concentration — Maximum ion concentration in cathode
`22806` `mol/m^3` (default) | positive scalar

Cathode maximum stoichiometry — Maximum stoichiometry in cathode
`0.74` (default) | positive scalar

Cathode minimum stoichiometry — Minimum stoichiometry in cathode
`0.035` (default) | positive scalar

Diffusion coefficient of anode active material — Diffusion coefficient of active material in anode
`3E-15` `m^2/s` (default) | positive scalar

Diffusion coefficient of cathode active material — Diffusion coefficient of active material in cathode
`5.9E-20` `m^2/s` (default) | positive scalar

Anode conductivity — Conductivity of anode
`100` `S/m` (default) | positive scalar

Cathode conductivity — Conductivity of cathode
`0.5` `S/m` (default) | positive scalar

Current collector resistance — Resistance of current collector
`0` `Ohm` (default) | nonnegative scalar

Volume fraction of electrolyte in anode — Fraction of volume of electrolyte in anode
`0.3874` (default) | scalar in the range (0,1)

Volume fraction of electrolyte in separator — Fraction of volume of electrolyte in separator
`0.45` (default) | scalar in the range (0,1)

Volume fraction of electrolyte in cathode — Fraction of volume of electrolyte in cathode
`0.5725` (default) | scalar in the range (0,1)

Electrolyte conductivity — Conductivity of electrolyte
`0.29` `S/m` (default) | positive scalar

Anode Bruggeman exponent — Bruggeman exponent of anode
`1.5` (default) | scalar greater than or equal to 1

Separator Bruggeman exponent — Bruggeman exponent of separator
`1.5` (default) | scalar greater than or equal to 1

Cathode Bruggeman exponent — Bruggeman exponent of cathode
`1.5` (default) | scalar greater than or equal to 1

Transference number — Fraction of total electric current that ion carries in electrolyte
`0.363` (default) | scalar in the range [0,1]

Diffusion coefficient of electrolyte — Diffusion coefficient of electrolyte
`2E-10` `m^2/s` (default) | positive scalar

Charge transfer rate constant for Anode — Rate constant of charge transfer for anode
`8.8E-11` `m^(5/2)/(mol^(1/2)*s)` (default) | positive scalar

Charge transfer rate constant for Cathode — Rate constant of charge transfer for cathode
`2.8E-13` `m^(5/2)/(mol^(1/2)*s)` (default) | positive scalar

Battery thermal mass — Thermal mass of battery associated with thermal port
`77` `J/K` (default) | positive scalar

Arrhenius reference temperature — Arrhenius reference temperature
`298.15` `K` (default) | positive scalar

Activation energy for diffusion in anode active material — Activation energy for diffusion inside active material of anode
`39000` `J/mol` (default) | positive scalar

Activation energy for diffusion in cathode active material — Activation energy for diffusion inside active material of cathode
`35000` `J/mol` (default) | positive scalar

Activation energy for diffusion in electrolyte — Activation energy for diffusion inside electrolyte
`26600` `J/mol` (default) | positive scalar

Activation energy for conduction in anode — Activation energy for conduction inside anode
`3000` `J/mol` (default) | positive scalar

Activation energy for conduction in cathode — Activation energy for conduction inside cathode
`3000` `J/mol` (default) | positive scalar

Activation energy for conduction in electrolyte — Activation energy for conduction inside electrolyte
`11000` `J/mol` (default) | positive scalar

Activation energy for charge transfer in Anode — Activation energy for charge transfer inside anode
`13000` `J/mol` (default) | positive scalar

Activation energy for charge transfer in Cathode — Activation energy for charge transfer inside cathode
`20000` `J/mol` (default) | positive scalar

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.