Isothermal Liquid Properties (IL)
Physical properties of isothermal liquid
Libraries:
Simscape /
Foundation Library /
Isothermal Liquid /
Utilities
Description
The Isothermal Liquid Properties (IL) block defines the liquid properties that act as global parameters for all the blocks connected to a circuit. The default liquid is water.
Each topologically distinct isothermal liquid circuit in a diagram can have a Isothermal Liquid Properties (IL) block connected to it. If no Isothermal Liquid Properties (IL) block is attached to a circuit, the blocks in this circuit use the properties corresponding to the default Isothermal Liquid Properties (IL) block parameter values.
The Isothermal Liquid Properties (IL) block provides a choice of modeling options:
Mixture bulk modulus: either constant or a linear function of pressure
Entrained air: zero, constant, or a linear function of pressure
Equations used to compute various liquid properties depend on the selected isothermal liquid model. For detailed information, see Isothermal Liquid Modeling Options.
Ideal Fluid Models
Entrained air is the relative amount of nondissolved gas trapped in the fluid. Fluid with zero entrained air is ideal, that is, it represents pure liquid.
In its default configuration, the Isothermal Liquid Properties (IL) block models an ideal fluid with a constant bulk modulus:
Isothermal bulk modulus model is
ConstantEntrained air model is
ConstantEntrained air-to-liquid volumetric ratio at atmospheric pressure is
0
In this model, the liquid bulk modulus is assumed to be constant and therefore the liquid density increases exponentially with the liquid pressure:
where:
βL is liquid bulk modulus.
ρL is liquid density.
ρL0 is liquid density at reference pressure.
p is liquid pressure.
p0 is reference pressure. By default, the block assumes reference pressure to be the atmospheric pressure,
0.101325 MPa, but you can specify a different value.
In systems where the liquid pressure can change over a wide range, and the assumption of constant bulk modulus is not valid anymore, you can use the Isothermal bulk modulus model parameter to define the liquid bulk modulus as a linear function of pressure:
where:
βL0 is liquid bulk modulus at reference pressure.
Kβp is the coefficient of proportionality between the bulk modulus and pressure increase.
If liquid pressure decreases below the reference pressure p0, the liquid bulk modulus value in the previous equation can become negative, which is nonphysical. To ensure that the liquid bulk modulus always stays positive, use the Minimum valid pressure parameter to specify the minimum valid pressure, pmin:
If liquid pressure drops below the Minimum valid pressure parameter value, simulation issues an error.
Fluid Models with Entrained Air
In practice, working fluid is a mixture of liquid and a small amount of entrained air.
To model this type of fluid, specify a nonzero value for the Entrained
air-to-liquid volumetric ratio at atmospheric pressure parameter, but keep the
Entrained air model as Constant.
The mixture density at a given pressure is defined as the total mass of liquid and entrained air over the total volume of the liquid and the entrained air at that pressure. While the total mass of the mixture is conserved as the pressure changes, the mixture volume does not stay constant. The entrained air is given by a volumetric fraction:
where:
α0 is entrained air-to-liquid volumetric ratio at reference (atmospheric) pressure.
Vg0 is air volume at reference pressure.
VL0 is pure liquid volume at reference pressure.
The entrained air is assumed to follow the ideal gas law. The compression or expansion of air in the liquid is a polytropic process, in which the air pressure and liquid pressure are identical:
where:
Vg is air volume.
n is air polytropic index.
To model the air dissolution effects into the fluid, select the Model air dissolution check box.
The process of dissolving air into the fluid is described by Henry’s law. At pressures less than or equal to the reference pressure, p0 (which is assumed to be equal to atmospheric pressure), all the air is assumed to be entrained. At pressures equal or higher than pressure pc, all the entrained air has been dissolved into the liquid. At pressures between p0 and pc, the volumetric fraction of entrained air that is not lost to dissolution, θ(p), is a linear function of the pressure, and is approximated by a third-order polynomial function to smoothly connect the density and bulk modulus values between the three pressure regions:
Data Visualization
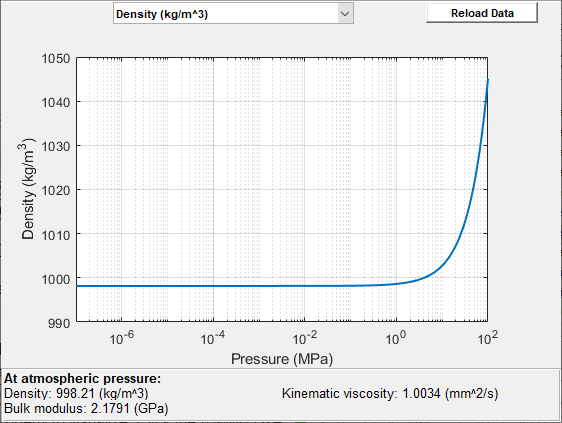
The block provides the option to plot the specified fluid properties (density and isothermal bulk modulus) as a function of pressure. Plotting the properties lets you visualize the data before simulating the model.
To plot the data, right-click the Isothermal Liquid Properties (IL) block in your model and, from the context menu, select Foundation Library > Plot Fluid Properties. Use the drop-down list located at the top of the plot to select the fluid property to visualize. Click the Reload button to regenerate a plot following a block parameter update.
Isothermal Liquid Properties Plot