Configure the S-Function Builder Settings

Specify the number of discrete states and their initial conditions, the sample mode, and the sample time of the S-function. This example contains two discrete states, each initialized to 1, and a discrete sample mode with a sample time of 1. Ensure that the Direct feedthrough is selected, because the current values of the S-function inputs are used to compute its outputs.

Define Ports and Parameters

Use the Ports and Parameters table on the bottom of the editor to specify the ports and parameters of the S-function. For this example, we have one input, one output port, and four parameters.

To set or change the values of the block parameters, you can:

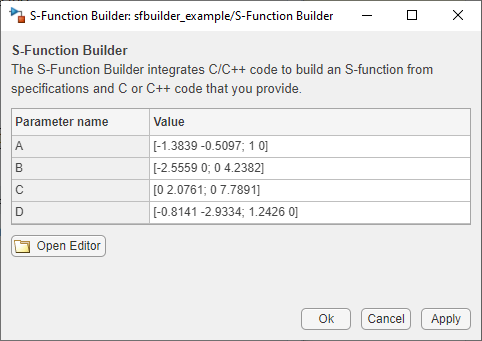
Alternatively, you can store the state-space matrices in variables in the MATLAB^® workspace and enter the variable names into the Value field for each parameter. Enter the values in the image for state-space parameters on the Value field of the Block Parameters table.

Define the Output Method

In this example, The Outputs_wrapper method calculates the S-function output as a function of the input and state vectors and the state-space matrices. In the outputs code, reference S-function parameters using the parameter names defined on the Ports and Parameters table. Index into 2-D matrices using a scalar index, again keeping in mind that S-functions use zero-based indexing. For example, to access the element C(2,1) in the S-function parameter C, use C[1]in the S-function code.

void dsfunc_builder_Outputs_wrapper(const real_T *u,
                                real_T *y,
                                const real_T *xD,
                                const real_T *xC,
                                const real_T *A, const int_T p_width0,
                                const real_T *B, const int_T p_width1,
                                const real_T *C, const int_T p_width2,
                                const real_T *D, const int_T p_width3)
{
/* Output_BEGIN */
    y[0]=C[0]*xD[0]+C[2]*xD[1]+D[0]*u[0]+D[2]*u[1];
    y[1]=C[1]*xD[0]+C[3]*xD[1]+D[1]*u[0]+D[3]*u[1];
/* Output_END */
}

Define the Update Method

The Update_wrapper method updates the discrete states. As with the outputs code, use the S-function parameter names and index into 2-D matrices using a scalar index, keeping in mind that S-functions use zero-based indexing. For example, to access the element A(2,1) in the S-function parameter A, use A[1]in the S-function code. The variable xD stores the final values of the discrete states. Enter the following code in the Update_wrapper function.

void dsfunc_builder_Update_wrapper(const real_T *u,
                               real_T *y,
                               real_T *xD,
                               const real_T *A, const int_T p_width0,
                               const real_T *B, const int_T p_width1,
                               const real_T *C, const int_T p_width2,
                               const real_T *D, const int_T p_width3)
{
/* Update_BEGIN */
    real_T   tempX[2] = {0.0, 0.0};
    tempX[0]=A[0]*xD[0]+A[2]*xD[1]+B[0]*u[0]+B[2]*u[1];
    tempX[1]=A[1]*xD[0]+A[3]*xD[1]+B[1]*u[0]+B[3]*u[1];
   			 
    xD[0] = tempX[0];
    xD[1] = tempX[1];
/* Update_END */
}

Build the State-Space System

Click the arrow under Build and select the following options:

To learn more about what each option does, see Build S-Functions Automatically Using S-Function Builder.

To build your S-function, click Build on the toolstrip to create an executable file for this S-function. You can now run the model and compare the output to the original discrete state-space S-function contained in sfcndemo_dsfunc.