Developing the Apollo Lunar Module Digital Autopilot

This example uses:

"Working on the design of the Lunar Module digital autopilot was the highlight of my career as an engineer. When Neil Armstrong stepped off the LM (Lunar Module) onto the moon's surface, every engineer who contributed to the Apollo program felt a sense of pride and accomplishment. We had succeeded in our goal. We had developed technology that never existed before, and through hard work and meticulous attention to detail, we had created a system that worked flawlessly." -Richard J. Gran, The Apollo 11 Moon Landing: Spacecraft Design Then and Now.

This example shows how Richard and the other engineers who worked on the Apollo Lunar Module digital autopilot design team could have done it using Simulink® and Aerospace Blockset™ if they had been available in 1961.

Model Description

Developing the autopilot in Simulink takes a fraction of the time it took for the original design of the Apollo Lunar Module autopilot.

if ~bdIsLoaded("aero_dap3dof")
    open_system("aero_dap3dof");
end

Figure Apollo Lunar Module Descent Animation contains objects of type hgjavacomponent, uimenu, uipanel, uitoolbar.

Lunar module digital autopilot design model

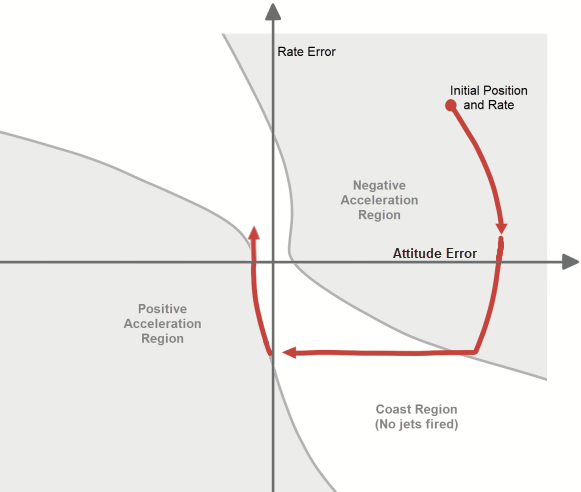
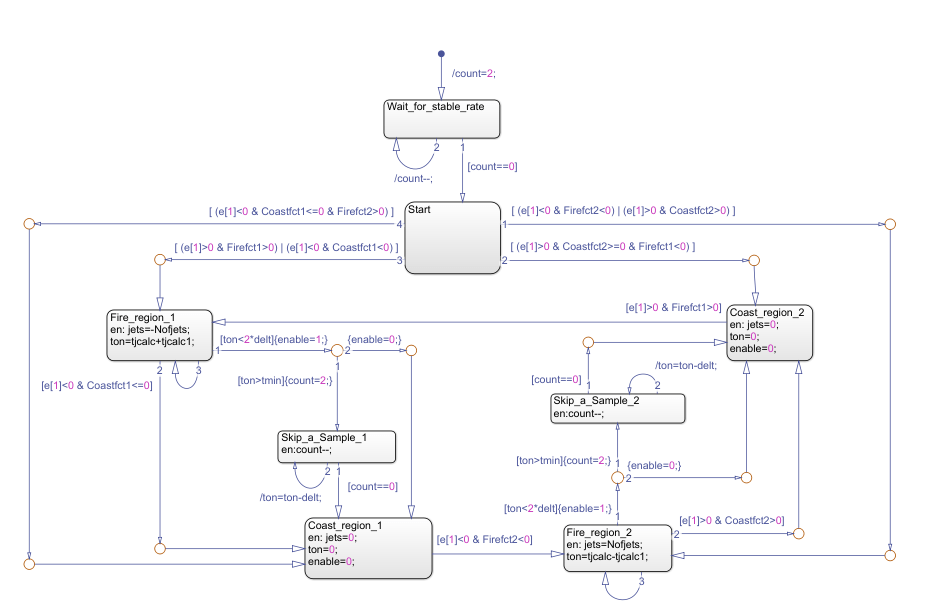
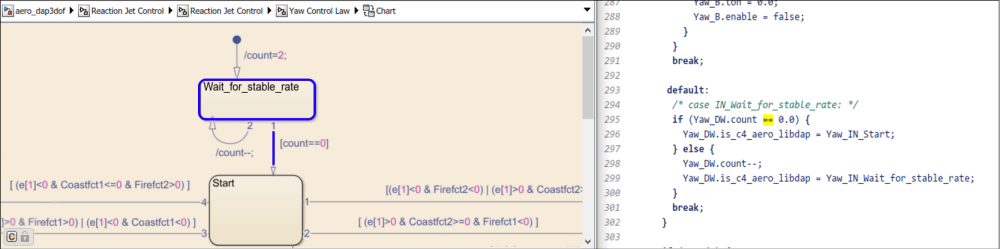
The Reaction Jet Control subsystem models the digital autopilot design proposed (and implemented) by MIT Instrumentation Laboratories (MIT IL), now called Draper Laboratory. A Stateflow® diagram in the model specifies the logic that implements the phase-plane control algorithm described in the technical article The Apollo 11 Moon Landing: Spacecraft Design Then and Now. Depending on which region of the diagram the Lunar Module is executing, the Stateflow diagram is in either a Fire_region or a Coast_region. Note, the transitions between these different regions depend on certain parameters. The Stateflow diagram determines whether to transition to another state and then computes which reaction jets to fire.

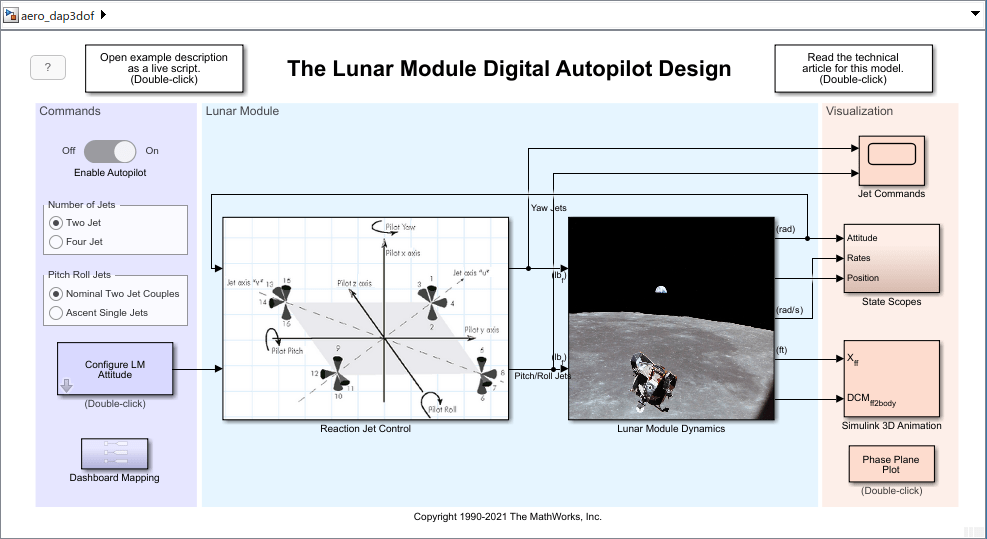
DevelopingTheApolloLunarModuleDigitalAutopilotExample_08.png

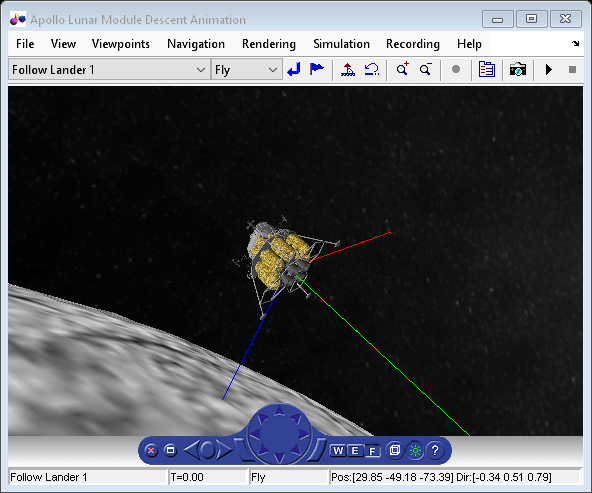
Translational and rotational dynamics of the Lunar Module are approximated in the Lunar Module Dynamics subsystem. Access various visualization methods of the Lunar Module states and autopilot performance in the Visualization area of the model, including Simulink scopes, animation with Simulink 3D Animation™, and a phase plane plot.

Phase plane plot for lunar module year axis digital control and animation with Simulink 3D Animation

Interactive Controls

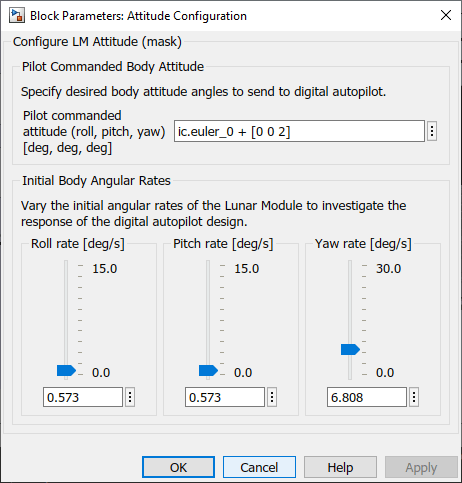
To interact with the Lunar Module model, vary autopilot settings and Lunar Module initial states in the Commands area. For example, to observe how the digital autopilot design handles increased initial body rates, use the slider components in Configure LM Attitude.

Interactive controls for lunar module model

Mission Description

The LM digital autopilot has three degrees of freedom. This means that by design, the reaction jet thrusters are configured and commanded to rotate the vehicle without impacting the vehicle's orbital trajectory. Therefore, the translational dynamics in his model are approximated via orbit propagation using the Spacecraft Dynamics block from Aerospace Blockset. The block is configured to use Moon spherical harmonic gravity model LP-100K.

LM digital autopilot subsystem block

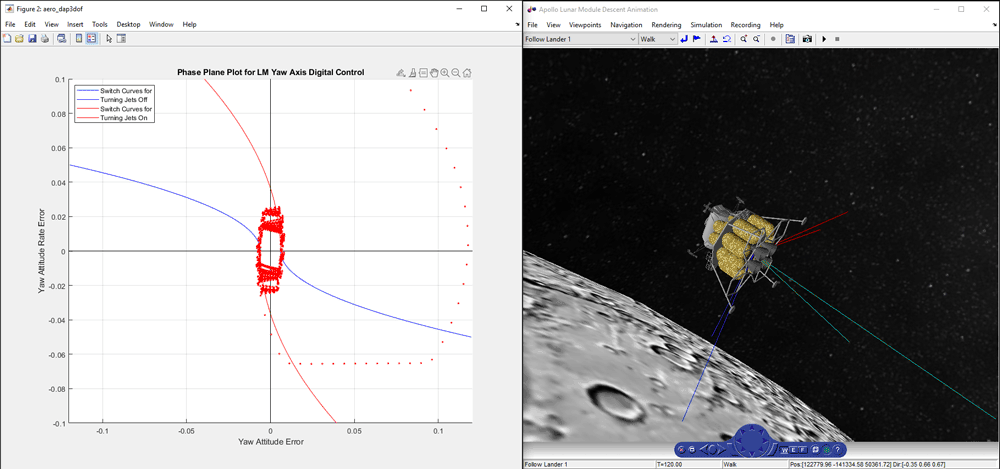
To demonstrate the digital autopilot design behavior, the "Descent Orbit Insertion" mission segment, just prior to the initiation of the powered descent, was selected from the Apollo 11 Mission Report.

Graphic of descent orbit insertion

(Image Credit: NASA)

The "Descent Orbit Insertion" burn began 101 hours, 36 minutes, and 14 seconds after lift-off and lasted 30 seconds. The burn set the Lunar module on a trajectory to lower its orbit from approximately 60 nautical miles to 50,000 ft over about an hour. At 50,000 ft, the Module initiated its powered descent.

Initialize the model aero_dap3dof with the approximate trajectory of the Lunar Module immediately after the descent orbit insertion burn.

mission.t_rangeZero             = datetime(1969,7,16,13,32,0); % lift-off
mission.t_descentInsertionStart = mission.t_rangeZero + hours(101) + minutes(36) + seconds(14);
mission.t_descentInsertion      = mission.t_descentInsertionStart + seconds(30);
mission.t_poweredDescentStart   = mission.t_rangeZero + hours(102) + minutes(33) + seconds(5.2);

disp(timetable([mission.t_rangeZero, mission.t_descentInsertionStart, ...
    mission.t_descentInsertion, mission.t_poweredDescentStart]', ...
    {'Range Zero (lift-off)', 'Descent Orbit Insertion (Engine ignition)', ...
    'Descent Orbit Insertion (Engine cutoff)', 'Powered Descent (Engine ignition)'}', VariableNames="Mission Phase"));

            Time                            Mission Phase                
    ____________________    _____________________________________________

    16-Jul-1969 13:32:00    {'Range Zero (lift-off)'                    }
    20-Jul-1969 19:08:14    {'Descent Orbit Insertion (Engine ignition)'}
    20-Jul-1969 19:08:44    {'Descent Orbit Insertion (Engine cutoff)'  }
    20-Jul-1969 20:05:05    {'Powered Descent (Engine ignition)'        }

The trajectory of the module at "Descent Orbit Insertion (Engine cutoff)" and "Powered Descent Initiation (Engine ignition)" is provided in the Apollo 11 Mission Report (Table 7-II.- Trajectory Parameters).

mission.Latitude_deg  = [-1.16, 1.02]';    % [deg]
mission.Longitude_deg = [-141.88, 39.39]'; % [deg]
mission.Altitude_mi   = [57.8, 6.4]';      % [nautical miles]
mission.Altitude_ft   = convlength(mission.Altitude_mi, 'naut mi', 'ft');
mission.Velocity_fps  = [5284.9, 5564.9]'; % [ft/s] (in Inertial frame)
mission.FlightPathAngle_deg = [-0.06, 0.03]'; % [deg] (measured upward from local horizontal plane)
mission.HeadingAngle_deg = [-75.19 -101.23]'; % [deg] (measured East of North)
disp(table({'Range Zero (lift-off)'; 'Descent Orbit Insertion (Engine ignition)'}, ...
    mission.Latitude_deg, mission.Longitude_deg, mission.Altitude_mi, ...
    mission.Velocity_fps, mission.FlightPathAngle_deg, mission.HeadingAngle_deg, ...
    VariableNames=["Mission Phase", ...
    "Latitude (deg)", "Longitude (deg)", "Altitude (mi)", ...
    "Velocity (ft/s)", "Flight path angle (deg)", "Heading (deg)"]));

                    Mission Phase                    Latitude (deg)    Longitude (deg)    Altitude (mi)    Velocity (ft/s)    Flight path angle (deg)    Heading (deg)
    _____________________________________________    ______________    _______________    _____________    _______________    _______________________    _____________

    {'Range Zero (lift-off)'                    }        -1.16             -141.88            57.8             5284.9                  -0.06                 -75.19   
    {'Descent Orbit Insertion (Engine ignition)'}         1.02               39.39             6.4             5564.9                   0.03                -101.23

Model Initialization

Initialize model parameters for the mission phase "Descent Orbit Insertion (Engine cutoff)" using the data defined above.

The initialization function aero_dap3dofdata requires information about the orientation of the Moon, which can be calculated using the Aerospace Blockset function moonLibration. This function requires "Ephemeris Data for Aerospace Toolbox". Use aeroDataPackage to install this data if it is not already installed.

mission.LibrationAngles_deg = moonLibration(juliandate(mission.t_descentInsertion), "405");

This example uses saved libration angle data corresponding with t_descentInsertion. Use the above command after installing the required ephemeris data.

mission.LibrationAngles_deg = [0.006379917345247; 0.382328074214300; 6.535718297208969];

Run the initialization function:

[moon, ic, vehicle, rcs] = aero_dap3dofdata(...
    mission.Latitude_deg(1), mission.Longitude_deg(1), mission.Altitude_ft(1), ...
    mission.Velocity_fps(1), mission.FlightPathAngle_deg(1), ...
    mission.HeadingAngle_deg(1), mission.LibrationAngles_deg)

moon = struct with fields:
    r_moon_eq: 5702428
       f_moon: 0.0012

ic = struct with fields:
       t_runtime: 120
    pos_inertial: [-3.6488e+06 -4.4381e+06 -1.9070e+06]
    vel_inertial: [4.0625e+03 -3.3792e+03 86.4867]
         euler_0: [-30 -10 -60]

vehicle = struct with fields:
    inertia_0: [3x3 double]
       mass_0: 33296

rcs = struct with fields:
     Force: 100
     L_arm: 5.5000
        DB: 0.0060
      tmin: 0.0140
     alph1: 0.0550
     alph2: 0.0039
     alph3: 0.0050
     alphu: 0.0063
     alphv: 7.8553e-04
    alphs1: 0.0055
    alphsu: 6.2855e-04
    alphsv: 7.8553e-05
    clockt: 0.0050
      delt: 0.1000

Closing Remarks

Building a digital autopilot was a daunting task in 1961 because there was very little industrial infrastructure for it - everything about it was in the process of being invented. Here is an excerpt from the technical article The Apollo 11 Moon Landing: Spacecraft Design Then and Now:

"One reason why the [autopilot's machine code] was so complex is that the number of jets that could be used to control the rotations about the pilot axes was large. A decision was made to change the axes that the autopilot was controlling to the "jet axes" shown in aero_dap3dof. This change dramatically reduced the number of lines of code and made it much easier to program the autopilot in the existing computer. Without this improvement, it would have been impossible to have the autopilot use only 2000 words of storage. The lesson of this change is that when engineers are given the opportunity to code the computer with the system they are designing, they can often modify the design to greatly improve the code."

References

[1] National Aeronautics and Space Administration Manned Spacecraft Center, Mission Evaluation Team. (November 1969). Apollo 11 Mission Report MSC-00171. Retrieved from https://www.nasa.gov/specials/apollo50th/pdf/A11_MissionReport.pdf

[2] Richard J. Gran, MathWorks. (2019). The Apollo 11 Moon Landing: Spacecraft Design Then and Now. Retrieved from https://www.mathworks.com/company/technical-articles/the-apollo-11-moon-landing-spacecraft-design-then-and-now.html