使用使能子系统实现控制算法
此示例说明如何使用使能子系统基于二进制逻辑信号实现控制算法。当二进制信号具有正值时,使能子系统执行并实现控制算法。在此示例中,使用超螺旋控制算法来稳定不稳定的动态系统。超螺旋算法是以稳健性能闻名的滑动模式控制方法之一。
打开模型。
mdl = "enablesub.slx";
open_system(mdl)
动态系统
所考虑的动态系统由以下方程控制:
是控制输入, 是外部扰动。
控制器和控制信号
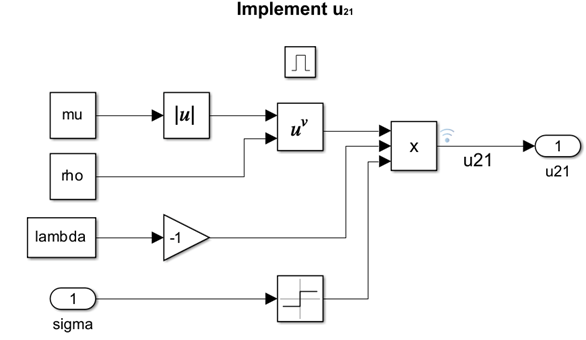
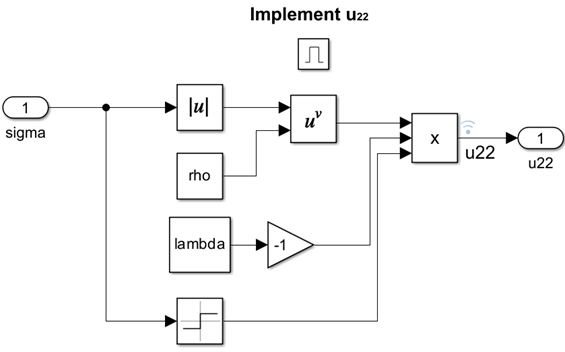
控制输入 () 有两个组件,即 和 ,它们由超螺旋算法控制。 的基于逻辑的设计是使用使能子系统实现的。
、 和 。这些参数从模型回调参数 PreLoadFcn 加载。
运行仿真并可视化结果
运行仿真并使用 Scope 模块和 Simulink 数据检查器可视化结果。
out = sim(mdl);
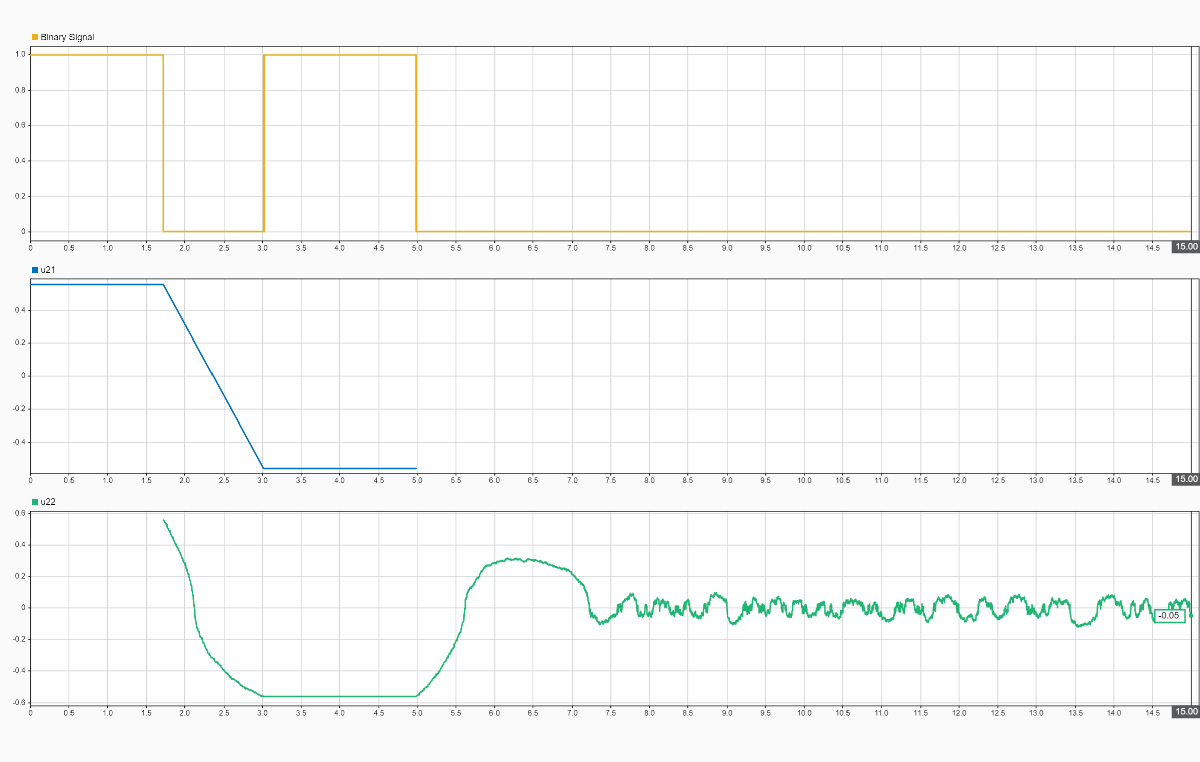
可视化控制器输入
Simulink 数据检查器显示基于二进制信号的子系统输出。输出 和 是控制器增益 的两个组件。
包含 的子系统在 0 到 1.8 秒之间和 3 到 5 秒之间启用。
包含 的子系统在 1.8 到 3 秒之间和 5 到 15 秒之间启用。
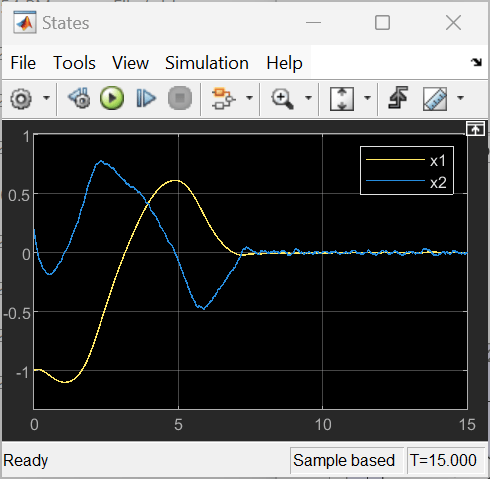
状态输出
状态输出显示控制器稳定了系统。
另请参阅
Enabled Subsystem | From | Goto | Integrator | Saturation
主题
参考
[1] Shtessel, Yuri, Christopher Edwards, Leonid Fridman, and Arie Levant. "Sliding mode control and observation." Vol. 10. New York: Springer New York, 2014. https://link.springer.com/book/10.1007/978-0-8176-4893-0