Main Content

自动气候控制系统仿真

此示例使用:

打开模型

此示例说明如何使用 Simulink® 和 Stateflow® 对汽车中自动气候控制系统进行仿真。

  • 在 User Setpoint in Celsius 模块中，输入车内所需的气温值。

  • 在 External Temperature in Celsius 模块中，输入外部气温值。

  • Thermometer Display 模块指示安装在驾驶员头部后面的温度传感器的读数。这是驾驶员感受到的温度。

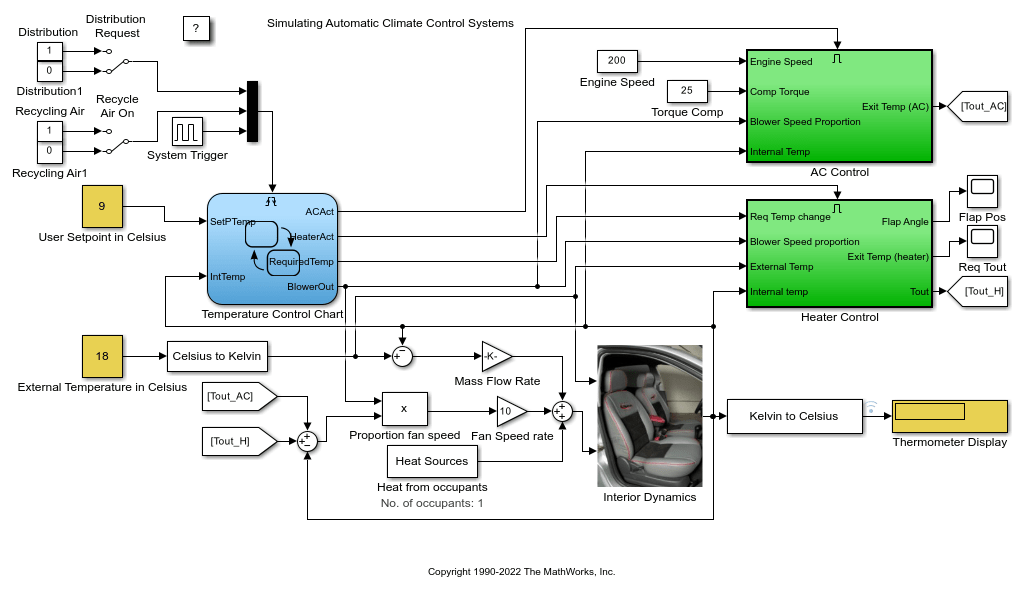
图 1：自动气候控制系统。

Stateflow® 控制器

Stateflow 实现监督控制器。要查看控制逻辑，请打开图。

Heater_AC 状态显示，输入的设定点温度比车内当前温度高至少 0.5 摄氏度时，加热器系统会打开。加热器保持活动状态，直到车内的当前温度在设定温度的上下 0.5 摄氏度范围内。同样，当输入比当前车内温度低 0.5 摄氏度（或更低）的设定点时，空调会打开。空调将保持活动状态，直到车内气温在设定温度上下 0.5 摄氏度范围内。为了避免连续打开和关闭加热器，该逻辑实现一个 0.5 摄氏度的死区。

在 Blower 状态下，设定点温度和当前温度之间的差值越大，风扇吹得越强劲。这可确保温度在合理时间内达到要求的值（即使存在温差）。当车内气温在设定温度上下 0.5 摄氏度范围内时，系统将关闭。

两个开关触发控制 Air Distribution(AirDist) 和 Recycling Air (Recyc_Air) 状态的 Stateflow 图。为了便于对车窗进行有效除霜，控制器在这两种状态下实现内部转移。当除霜状态激活时，控制器关闭空气循环功能。

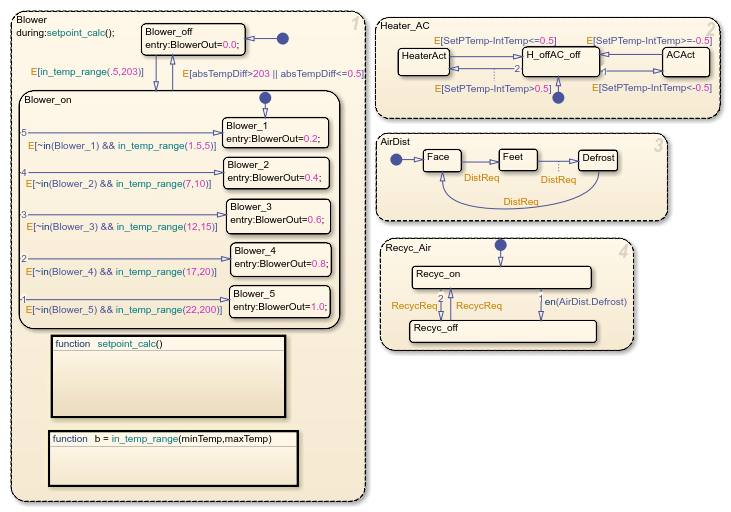
图 2：Stateflow 中的监督控制逻辑。

加热器和空调模型

加热器模型实现以下热交换方程：

Tout = Ts - (Ts-Tin)e^[(-pi*D*L*hc)/(m_dot*Cp)]

其中：

  • Ts = 常量（散热器壁温）

  • D = 0.004m（通道直径）

  • L = 0.05m（散热器厚度）

  • N = 30000（通道数）

  • k = 0.026 W/mK = 常量（空气的热导率）

  • Cp = 1007 J/kgK = 常量（空气的比热）

  • 层流 (hc = 3.66(k/D) = 23.8 W/m2K)

模型说明加热器挡板的工作原理。与吹风机的运行类似，所需设定点温度和车内当前温度之间的温差越大，加热效果越大。

空调模型实现以下方程：

y*(w*Tcomp) = m_dot*(h4-h1)

其中：

  • y = 效率

  • m_dot = 质量流量

  • w = 发动机的转速

  • Tcomp = 压缩机扭矩

  • h4、h1 = 焓

空调系统的 Bang-Bang 控制使用发动机转速和压缩机扭矩来确定空调吹出的气温。

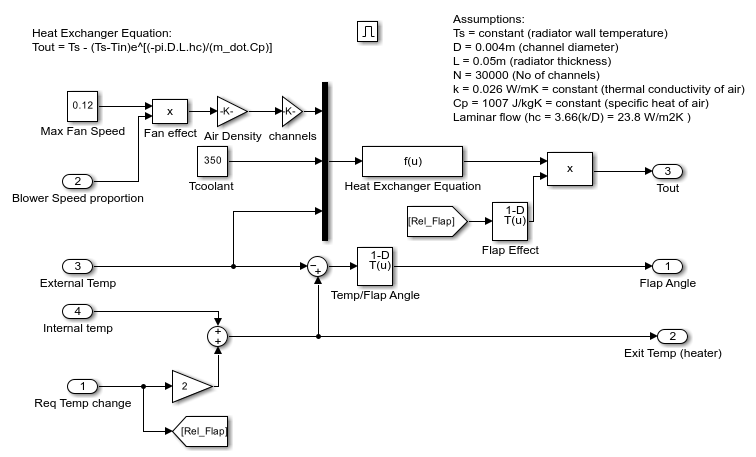
图 3：加热器控制子系统。

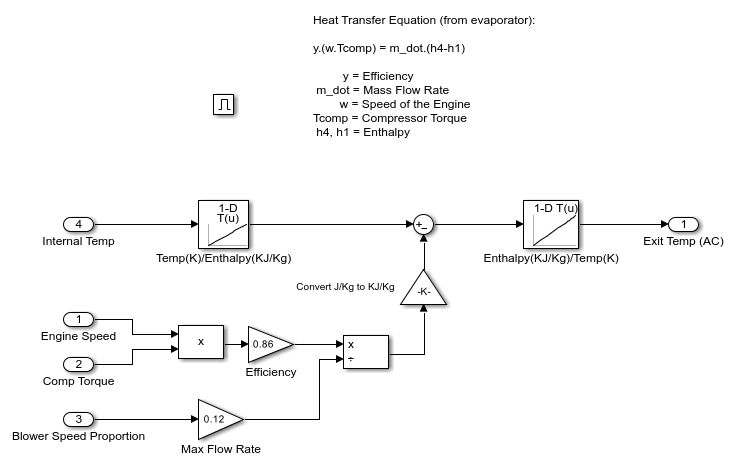
图 4：空调控制子系统。

车舱热传递

下列因素会影响驾驶员感受到的气温：

  • 通风口吹出的气温

  • 室外气温

  • 车内人数

这些因素是车舱内部的热力学模型的输入。为了计算从通风口吹出的气温，该模型计算通风口气温和车内当前温度之间的差值，并将其乘以风扇速度比例（质量流量）。该模型针对车内每个乘客增加 100 W 的能量。为了计算从车外到车内的空气辐射，该模型将车内外气温之差乘以较小的质量流量。

Thermometer Display 模块显示内部动态模型输出。它是安装在驾驶员头部后面的温度传感器的读数。如果使用默认设置运行仿真，温度读数从车外温度 18 °C 开始，然后冷却至用户设定值点 9 °C。

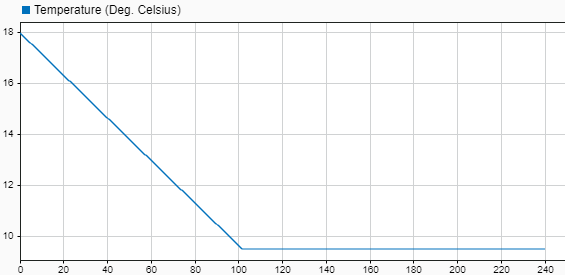
图 5：时间-温度计显示图

相关主题