比较求解器
求解器通过使用模型提供的信息,计算动态系统在指定时间范围内连续时间步的状态,从而对动态系统进行仿真。根据系统模型计算系统连续状态的过程称为解算模型。没有任何一种模型解算方法可满足所有系统需要。因此,Simulink® 提供一组称为求解器的程序,每个程序都利用一种特定方法来解算模型。“配置参数”对话框允许您选择最适合您的模型的求解器。
定步长和变步长求解器
您可以根据 Simulink 提供的求解器计算步长的方式来选择求解器:定步长和变步长。
定步长求解器按固定时间间隔在从仿真开始到仿真结束的时间段内解算模型。间隔的大小称为步长。您可以指定步长,也可以让求解器选择步长。一般情况下,减小步长将提高结果的准确性,但会增加系统仿真所需的时间。
变步长求解器会在仿真过程中改变步长。它们在模型状态快速变化时,会减小步长以提高准确性;当模型状态缓慢变化时,增加步长以避免执行不必要的时间步。计算步长会增加每个步长的计算开销,但可以减少对具有快速变化的状态或分段连续状态的模型维护指定级别的准确性所需的总时间步数,从而缩短仿真时间。
定步长和变步长求解器将下一个仿真时间计算为当前仿真时间与步长之和。求解器配置窗格上的类型控件用于选择求解器类型。对于定步长求解器,步长在仿真过程中保持不变。对于变步长求解器,每一个时间步的步长可能各不相同,具体情况取决于模型的动态特性。具体来讲,就是变步长求解器会增加或减少步长,以满足您指定的误差容限。
选择哪一种求解器取决于您计划如何部署模型以及模型的动态特性。如果您计划从模型中生成代码,然后在实时计算机系统上运行代码,请选择定步长求解器来进行模型仿真。您不能将变步长映射到实时时钟。
如果您不打算以生成代码的形式来部署模型,则选择变步长求解器还是定步长求解器取决于模型的动态特性。变步长求解器也许能显著缩短模型的仿真时间。变步长求解器之所以能够节省仿真时间,是因为求解器可以根据需要动态调整步长来达到给定级别的准确性。这种方法可以减少所需的步长数。定步长求解器必须根据准确性要求在整个仿真过程中使用一种步长。为了在整个仿真过程中满足这些要求,定步长求解器通常需要较小的步长。
例如,假设模型有两个采样时间,0.5 和 0.75。为了涵盖两个速率的执行,定步长求解器必须使用步长 0.25,这是两个采样时间的最小公分母。定步长仿真的时间步包括:
[0.0 0.25 0.5 0.75 1.0 1.25 1.5 ...]
变步长求解器可以对每个时间步采用不同步长。对于此模型,变步长求解器仅在具有每个采样时间的模块执行时执行一个时间步。变步长仿真的时间步包括:
[0.0 0.5 0.75 1.0 1.5 ...]
为了达到仿真时间 1.5,定步长仿真需要七个步骤,而变步长仿真只需五个步骤。随着模型复杂度和仿真持续时间的增加,变步长求解器可以显著减少仿真模型所需的时间步数。
连续与离散求解器
Simulink 同时提供连续和离散求解器。
选择求解器类型时,您还可以选择特定的求解器。两组求解器都包括离散求解器和连续求解器。离散和连续求解器依赖于模型的模块来计算任何离散状态的值。定义离散状态的模块负责计算这些状态在每个时间步的值。但是,与离散求解器不同,连续求解器运用数值积分方法来计算模块定义的连续状态。选择求解器时,首先要确定是要使用离散求解器,还是要使用连续求解器。
如果您的模型没有连续状态,Simulink 将切换到定步长离散求解器或变步长离散求解器。如果您的模型只有连续状态,或者同时具有连续状态和离散状态,请根据模型的动态特性从其余的求解器选项中选择一种连续求解器。否则,将产生错误。
连续求解器使用数值积分方法,根据模型在之前的时间步的状态和状态导数来计算模型在当前时间步的连续状态。连续求解器依赖单个模块来计算模型在每个时间步的离散状态值。
离散求解器主要用于解算纯离散模型。它们只计算模型的下一个仿真时间步。执行这种计算时,它们依赖于模型中的每个模块来更新其各个离散状态。它们不计算连续状态。
求解器库中包含两种离散求解器:定步长离散求解器和变步长离散求解器。默认情况下,定步长求解器会选择足够快的步长和仿真速率,以跟踪模型中速度最快的模块的状态变化。变步长求解器会调整仿真步长,以便与离散状态的实际变化速度保持同步。这种调整可以避免不必要的仿真步,并缩短多速率模型的仿真时间。有关详细信息,请参阅 系统和子系统中的采样时间。
注意
您必须使用连续求解器来解算同时包含连续和离散状态的模型,因为离散求解器无法处理连续状态。另一方面,如果您对没有状态或只具有离散状态的模型选择连续求解器,Simulink 软件将使用离散求解器。
显式与隐式连续求解器
您可以用以下方程表示显式系统:
对于任何给定的 x 值,您可以通过代换 f(x) 中的 x 并求解该方程来计算 。
形式的方程被认为是隐式的。对于任何给定的 值,您必须求解此方程来计算 。
线性隐式系统可以用以下方程表示
M(x) 称为质量矩阵, 是外力函数。当您在模型中使用物理建模模块时,系统将变成线性隐式系统。
虽然使用隐式或显式连续求解器都可以解算所有这些系统,但隐式求解器通常更适合解算刚性系统。显式求解器用于解算非刚性系统。对于常微分方程问题,如果所需的解变化缓慢,但存在变化很快的较接近解,则称为刚性问题。数值方法必须执行较小的时间步来解算此类系统。刚度涉及到效率问题。系统的刚度越强,显式求解器执行计算的时间越长。刚性方程组具有缓慢变化和快速变化两种连续动态。
与显式求解器相比,隐式求解器为振动行为提供更高的稳定性。但是,隐式求解器的计算开销也更高。它们在每个时间步使用类牛顿法生成雅可比矩阵并解算一组代数方程。为了减少这种额外的成本,隐式求解器提供了一个求解器雅可比矩阵方法参数,可以提高隐式求解器的仿真性能。有关详细信息,请参阅Choose a Jacobian Method for an Implicit Solver。解算线性隐式系统时,隐式求解器比显式求解器更高效。
单步与多步连续求解器
Simulink 求解器库中提供了单步和多步求解器。单步求解器使用上一个时间点 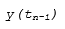 的解以及 tn 与 tn-1 之间的多个点的导数值来估算
的解以及 tn 与 tn-1 之间的多个点的导数值来估算 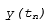 。这些点是子时间步。
。这些点是子时间步。
多步求解器使用前面几个时间步的结果来计算当前解。Simulink 提供一个显式多步求解器 ode113 和一个隐式多步求解器 ode15s。二者都是变步长求解器。
单阶与变阶连续求解器
这种区分基于求解器解算方程组时使用的阶次。求解器库中包含两个变阶求解器 ode15s 和 ode113。它们使用多阶来解算方程组。具体来讲,隐式变步长 ode15s 求解器使用一阶到五阶方程,而显式变步长 ode113 求解器使用一阶到十三阶方程。对于 ode15s,您可以通过最大阶数参数限制应用的最高阶次。有关详细信息,请参阅Maximum Order。
另请参阅
过零检测 | Simulink 模型 | 动态系统的仿真阶段