过零检测
变步长求解器可动态调整时间步大小,使其在某个变量缓慢变化时增加,在该变量迅速变化时减小。此行为使求解器在不连续点的附近执行许多小的时间步,因为该变量在此区域中迅速变化。这可以提高精确性,但可能会导致过多的仿真时间。
Simulink® 使用一种称为过零检测的技术来准确定位不连续性,无需借助于过小的时间步。通常这种方法可以缩短仿真运行时间,但它可能会导致某些仿真在预期完成时间之前停止。
Simulink 为此使用两种算法:非自适应算法和自适应算法。有关这些方法的信息,请参阅Zero-Crossing Algorithms。
仿真中过多的过零检测的影响
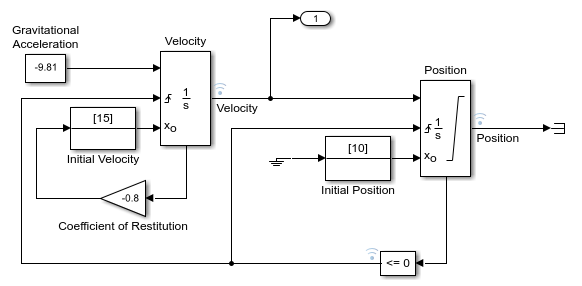
此示例使用模型 example_bounce_two_integrators 演示在仿真中过多的过零检测的影响,此模型使用两个 Integrator 模块对弹球的动力学特性进行建模。出于性能原因,建议尽可能使用 Second-Order Integrator 模块,而不是使用两个单独的 Integrator 模块。有关如何使用 Second-Order Integrator 模块对弹球的动力学特性进行建模的示例,请参阅弹球的仿真。
打开模型 example_bounce_two_integrators。
mdl = "example_bounce_two_integrators";
open_system(mdl)
要查看过多的过零检测的影响,请将模型配置为使用非自适应过零检测算法。
要打开“配置参数”对话框,请在 Simulink® 工具条中建模选项卡的设置下,点击模型设置。
在“配置参数”对话框的求解器窗格中,展开求解器详细信息。
在求解器详细信息中,在过零选项下,将算法参数设置为
Nonadaptive。点击确定。
或者,使用 set_param 函数将 ZeroCrossAlgorithm 参数设置为 Nonadaptive。
set_param(mdl,ZeroCrossAlgorithm="Nonadaptive")对模型进行仿真,直到 20 秒处的停止时间。
nonadaptive = sim(mdl,StopTime="20");绘制弹球的位置和速度。每次弹跳时,最大高度和最大速度都会降低。
nonadaptivePosition = getElement(nonadaptive.yout,"Position").Values; nonadaptiveVelocity = getElement(nonadaptive.yout,"Velocity").Values; tiledlayout(2,1) ax1 = nexttile; plot(nonadaptivePosition) grid(ax1,"on") title("Nonadaptive Zero-Crossing Detection Algorithm Results") ax2 = nexttile; plot(nonadaptiveVelocity) grid(ax2,"on") title("")

仅绘制最后一秒的仿真结果。在仿真的最后一秒,速度值接近零。
tiledlayout(2,1) ax1 = nexttile; plot(nonadaptivePosition) grid(ax1,"on") title("Nonadaptive Zero-Crossing Detection Algorithm Results") axis([19 20 0 0.11]) ax2 = nexttile; plot(nonadaptiveVelocity) grid(ax2,"on") title("") axis([19 20 -1.5 1.5])
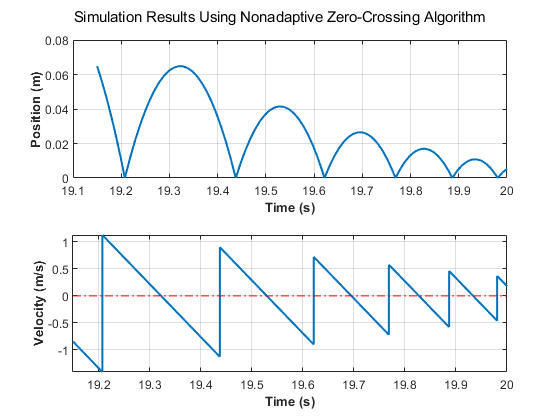
随着位置和速度值接近零,弹跳之间的时间间隔也会缩短。每次球弹跳时,位置和速度信号都会出现过零点。随着弹跳之间的时间间隔缩短,过零点变得更加频繁。
再次对模型进行仿真。这次,仿真的停止时间设为 25 秒,以观察非自适应过零算法如何处理仿真中频率增加的过零点。启用 CaptureErrors 参数以确保即使频繁的过零点在仿真中导致运行时错误,sim 函数仍返回结果。
nonadaptive25 = sim(mdl,StopTime="25",CaptureErrors="on");
要查看仿真停止的原因,请检查仿真元数据中的执行信息。
st = nonadaptive25.SimulationMetadata.ExecutionInfo.StopEventDescription
st =
'Simulink will stop the simulation of model 'example_bounce_two_integrators' because the 2 zero crossing signal(s) identified below caused 1000 consecutive zero crossing events in time interval between 20.357636989536076 and 20.357636990631594.
--------------------------------------------------------------------------------
Number of consecutive zero-crossings : 1000
Zero-crossing signal name : RelopInput
Block type : RelationalOperator
Block path : 'example_bounce_two_integrators/Compare To Zero/Compare'
--------------------------------------------------------------------------------
--------------------------------------------------------------------------------
Number of consecutive zero-crossings : 500
Zero-crossing signal name : x Lower Saturation
Block type : Integrator
Block path : 'example_bounce_two_integrators/Position'
--------------------------------------------------------------------------------
'
由于模型中名为 Compare To Zero 和 Position 的模块发生过多连续过零事件,导致运行时错误,仿真停止。
非自适应过零检测算法会围捕每个检测到的过零事件,以确定仿真期间发生的每个过零点的位置。尽管非自适应算法能够满足许多模型和仿真的要求,但在具有高度震颤或 Zeno 行为的系统中,非自适应算法会导致时间步之间的间隔非常小,仿真速度极慢。
如果过零信号值足够接近于零,并且连续过零点的数量已达到限制,自适应过零检测算法会停止围捕处理。如果自适应算法因过多的连续过零点而禁用围捕处理,默认情况下,仿真会发出关于忽略过零事件的警告。
尝试使用自适应过零检测算法对模型进行仿真,直到 25 秒处的停止时间。要隐藏关于忽略的过零点的警告,请将忽略的过零点参数设置为 none。
在“配置参数”对话框的求解器窗格中,在过零选项下,将算法参数设置为
Adaptive。在“配置参数”对话框的诊断窗格中,点击省略号以展开高级参数。然后,将忽略的过零点参数设置为
none。
或者,使用 set_param 函数将 ZeroCrossAlgorithm 参数设置为 Adaptive,并将 IgnoredZcDiagnostic 参数设置为 none。
set_param(mdl,ZeroCrossAlgorithm="Adaptive",IgnoredZcDiagnostic="none")
再次对模型进行仿真,直到 25 秒处的停止时间。启用 CaptureErrors 参数,以确保即使仿真因频繁过零点发出运行时错误,sim 函数仍返回结果。
adaptive = sim(mdl,StopTime="25",CaptureErrors="on");
要查看仿真停止的原因,请检查仿真元数据中的执行信息。
st = adaptive.SimulationMetadata.ExecutionInfo.StopEventDescription
st = 'Reached stop time of 25'
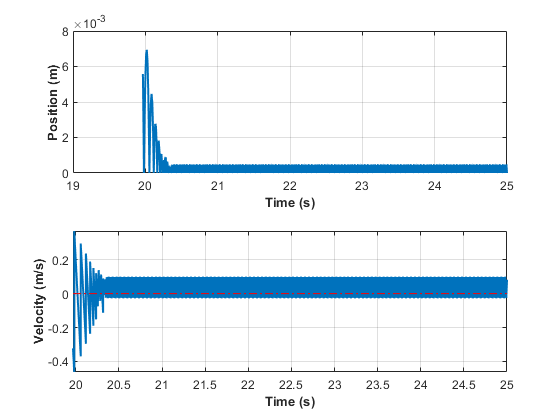
仿真在达到 25 秒处的停止时间后停止。绘制弹球的位置和速度。在 20 秒的仿真时间内,结果与使用非自适应过零检测算法的 20 秒仿真结果一致。在 20 秒后,位置和速度似乎均为零。
adaptivePosition = getElement(adaptive.yout,"Position").Values; adaptiveVelocity = getElement(adaptive.yout,"Velocity").Values; tiledlayout(2,1) ax1 = nexttile; plot(adaptivePosition) grid(ax1,"on") title("Adaptive Zero-Crossing Detection Algorithm Results") ax2 = nexttile; plot(adaptiveVelocity) grid(ax2,"on") title("")

仅绘制仿真结果的最后 5 秒。结果更完整,更接近控制弹球动力学特性的方程的预期解析解。随着系统状态值接近零,结果中的震颤在数值仿真的预期之内。
tiledlayout(2,1) ax1 = nexttile; plot(adaptivePosition) grid(ax1,"on") title("Adaptive Zero-Crossing Detection Algorithm Results") axis([20 25 0 0.01]) ax2 = nexttile; plot(adaptiveVelocity) grid(ax2,"on") title("") axis([20 25 -0.5 0.5])
防止过多过零
可以使用下表帮助您防止模型中出现过多过零错误。
| 更改类型 | 更改过程 | 优势 |
|---|---|---|
增加允许的过零数量 | 增加“配置参数”对话框中求解器窗格上连续过零点数选项的值。 | 这可能会给您的模型提供足够多的时间来解决过零情况。 |
放宽信号阈值 | 在“配置参数”对话框的求解器窗格上,从算法下拉列表中选择自适应,并增加信号阈值选项的值。 | 求解器需要较少的时间来准确定位过零点。这可以缩短仿真时间,并消除过多的连续过零错误数。不过,放宽信号阈值可能会降低精度。 |
使用自适应算法 | 在“配置参数”对话框的求解器窗格上,从算法下拉列表中选择自适应。 | 此算法会动态调整过零阈值,这可提高准确性,并减少检测到的连续过零点数。借助该算法,您可以同时指定时间容差和信号阈值。 |
对特定模块禁用过零检测 |
| 在本地禁用过零检测可以防止特定模块由于出现过多连续过零点而停止仿真。所有其他模块将继续受益于过零检测所提供的更高准确性。 |
对整个模型禁用过零检测 | 在“配置参数”对话框的求解器窗格上,从过零控制下拉列表中选择 | 这可防止在您模型中的任意位置检测到过零点。结果是您的模型将无法再受益于过零检测所提供的更高准确性。 |
如果使用 | 在“配置参数”对话框的求解器窗格上,从 | 有关详细信息,请参阅 Maximum order。 |
减小最大步长 | 在“配置参数”对话框的求解器窗格上,为 | 求解器可以采用足够小的步长来解决过零情况。但是,减小步长可能会增加仿真时间,在使用自适应算法时很少有必要这么做。 |
仿真器如何错过过零事件
弹球的仿真和Double Bouncing Ball: Use of Adaptive Zero-Crossing Location中的弹球和双弹球模型显示了有关不连续性的高频率波动(震颤)可能会导致仿真过早停止。
如果求解器误差容限太大,求解器还可能会完全错过过零点。这可能是因为过零检测方法会检查信号值在主时间步之后是否发生变化。符号变化指示出现过零,然后过零算法将搜索精确的过零时间。但是,如果某个时间步内发生过零,但该时间步开始和结尾的值没有指示符号变化,则求解器将越过过零而不检测它。
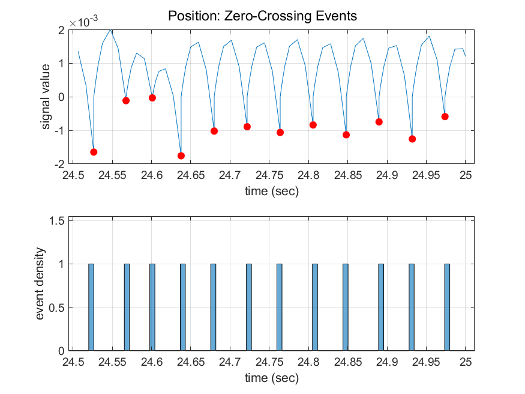
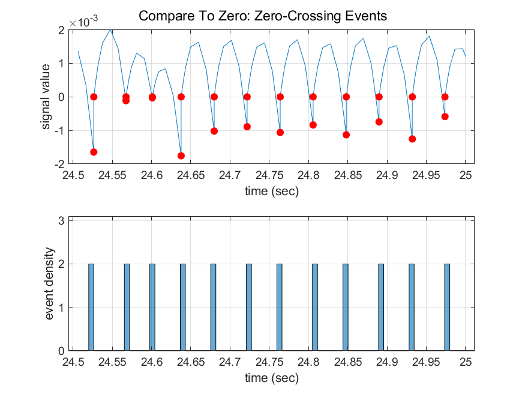
下图显示过零的信号。在第一个实例中,积分器越过该事件,因为符号在时间步之间没有变化。在第二实例中,求解器检测到符号变化,因此检测过零事件。

以弹球模型的双积分器实现为例。
使用求解器探查工具对仿真的最后 0.5 秒进行探查显示,仿真在 Compare To Zero 模块检测到 44 个过零事件,在 Position 模块的输出端检测到 22 个事件。

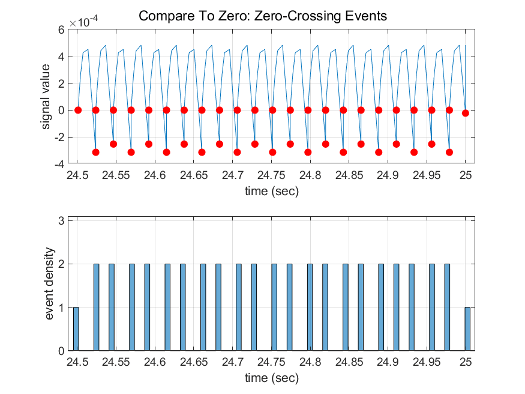
将相对容差参数的值增加到 1e-2,而不是默认的 1e-3。您可以在配置参数对话框的求解器窗格的求解器详细信息部分更改此参数,或使用 set_param 将 RelTol 指定为 '1e-2'。
用求解器的新相对容差对仿真的最后 0.5 秒进行探查,结果表明,它仅在 Compare To Zero 模块上检测到 24 个过零事件,在 Position 模块的输出端检测到 12 个事件。
模块中的过零检测
模块可以记录一系列过零变量,其中每个变量都是关于可能出现不连续点的状态变量的函数。当出现不连续点时,过零函数会发生由正值或负值穿过零值的相应情况。记录的过零变量将在每个仿真步的末尾更新,符号有变化的任何变量都将视为出现了过零事件。
如果检测到任何过零点,Simulink 软件会在符号有变化的每个变量的上一个值和当前值之间进行插值,以估计过零(即不连续点)时间。
注意
过零检测算法只能包含 double 数据类型的信号的过零事件。
记录过零点的模块
下表列出了记录过零点的模块,并解释了模块如何使用过零点。
| 模块 | 过零检测次数 |
|---|---|
一个:用于检测输入信号在上升或下降方向上过零的情况。 | |
两个,一个用于检测达到上阈值的情况,一个用于检测达到下阈值的情况。 | |
一个:用于检测信号等于常量的情况。 | |
一个:用于检测信号等于零的情况。 | |
两个:一个用于检测进入死区(输入信号减去下限)的情况,一个用于检测退出死区(输入信号减去上限)的情况。 | |
一个:如果 Enable 端口位于 Subsystem 模块内,它会提供过零检测功能。有关详细信息,请参阅使用使能子系统。 | |
一个:用于检测输入信号在上升或下降方向上出现不连续点的情况。 | |
一个:用于检测输入信号在上升或下降方向上出现不连续点的情况。 | |
一个或两个。如果没有任何输出端口,则只存在一个过零点,用于检测输入信号达到阈值的情况。如果有一个输出端口,将使用第二个过零点以便将输出从 1 恢复为 0,从而创建类似于冲激的输出。 | |
一个:用于检测满足 If 条件的情况。 | |
如果存在重置端口,则检测发生重置的情况。 如果输出是有限的,则存在三个过零点:一个用于检测达到饱和上限的情况,一个用于检测达到饱和下限的情况,另一个用于检测不再处于饱和状态的情况。 | |
一个:对于输出向量的每个元素,用于检测输入信号是新的最小值或最大值的情况。 | |
两个,一个检测上限,另一个检测下限 | |
一个:用于检测满足指定关系的情况。 | |
一个:如果中继处于关闭状态,则检测接通点。如果中继处于打开状态,则检测断开点。 | |
两个,一个用于检测达到或离开上限的情况,一个用于检测达到或离开下限的情况。 | |
两个,一个检测上限,另一个检测下限 | |
五个,两个用于检测达到状态 x 上限或下限的情况,两个用于检测达到状态 dx/dt 上限或下限的情况,一个用于检测离开饱和状态的情况。 | |
一个:用于检测输入跨越零点的情况。 | |
一个:用于检测输入信号在上升或下降方向上出现不连续点的情况。 | |
一个:用于检测步长时间。 | |
一个:用于检测发生开关条件的情况。 | |
一个:用于检测满足 case 条件的情况。 | |
一个:如果 Triggered 端口位于 Subsystem 模块内,它会提供过零检测功能。有关详细信息,请参阅使用触发子系统。 | |
两个,一个用于使能端口,一个用于触发端口。有关详细信息,请参阅:使用使能触发子系统 | |
一个:用于检测输入信号在上升或下降方向上出现不连续点的情况。 |
注意
过零检测还适用于使用连续时间模式的 Stateflow® 图。有关详细信息,请参阅 Configure a Stateflow Chart for Continuous-Time Simulation (Stateflow)。
实现示例:Saturation 模块
Saturation 模块是注册了过零的 Simulink 模块的一个示例。过零检测可以在 Saturation 模块中标识以下状态事件:
输入信号达到上限。
输入信号离开上限。
输入信号达到下限。
输入信号离开下限。
定义自己的状态事件的 Simulink 模块被视为具有内部过零点。使用 Hit Crossing 模块接收过零事件的显式通知。请参阅记录过零点的模块,获取包含过零点的模块列表。
状态事件检测取决于内部过零信号的构造。模块图无法访问此信号。对于 Saturation 模块,用于检测上限过零点的信号是 zcSignal = UpperLimit - u,其中 u 是输入信号。
过零信号具有方向特性,它可包含下列值:
上升沿 - 当信号上升到零或通过零时,或信号离开零并变为正值时,将出现一个过零事件。
下降沿 - 当信号下降到零或通过零时,或信号离开零并变为负值时,将出现一个过零事件。
任一沿 - 无论是发生上升还是下降情况,都出现过零事件。
对于 Saturation 模块的上限,过零的方向是任一沿。这样可以使用同一过零信号检测进入和离开饱和状态的事件。