弹球的仿真
此示例使用一个弹球的两个模型来说明对具有 Zeno 行为的混合动态系统进行建模的不同方法。一般来说,Zeno 行为的特征可非正式地表示为某些混合系统在有限时间间隔内发生无限数量的事件。球在失去能量的同时,球与地面发生碰撞的时间间隔越来越短。
混合动态系统
弹球模型是混合动态系统的一个示例。混合动态系统是既包括连续动态又包括离散转移的系统,其中系统动态可能会发生变化,状态值可能会有跳跃。弹球的连续动态特性由以下方程给出:
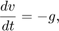
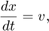
其中,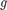 是重力加速度,
是重力加速度, 是球的位置,
是球的位置,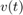 是速度。系统有两个连续状态:位置
是速度。系统有两个连续状态:位置  和速度
和速度  。
。
该模型的混合系统方面源于球与地面碰撞的建模。假设球与地面发生部分弹性碰撞,则碰撞前的速度 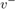 、碰撞后的速度
、碰撞后的速度  可以通过球的恢复系数
可以通过球的恢复系数  来关联,如下所示:
来关联,如下所示:
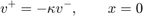
因此,弹球在转移条件 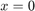 下显示连续状态(速度)下出现一个跳跃。此图显示球以 0 米/秒的速度从 25 米的高度向上抛。
下显示连续状态(速度)下出现一个跳跃。此图显示球以 0 米/秒的速度从 25 米的高度向上抛。

使用两个 Integrator 模块对弹球进行建模
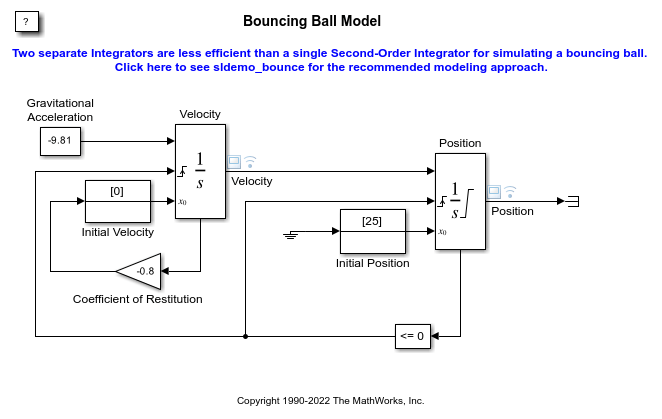
sldemo_bounce_two_integrators 模型使用两个 Integrator 模块对弹球进行建模。左边的 Integrator 模块是对第一个方程建模的速度积分器。右边的 Integrator 模块是位置积分器。打开位置积分器的“模块参数”对话框,会看到模块的下限为零。这种情况表示存在一个限制:球无法降到地面以下。
位置积分器的状态端口和对应的比较结果用于检测球何时落地并重置两个积分器。速度积分器的状态端口用于计算  。
。
要观察系统的 Zeno 行为,请修改求解器配置参数。
要打开“配置参数”对话框,请在建模选项卡的设置下,点击模型设置。
选择求解器窗格。
将停止时间设置为
25。点击求解器详细信息旁边的箭头,查看其他求解器参数。
在过零选项下,将算法设置为
Nonadaptive。
对模型进行仿真。
随着球更频繁地落地并损失能量,仿真超出默认的连续过零点数的限制 1000。
在“配置参数”对话框中,将算法设置为 Adaptive。此自适应算法包含一种对震颤行为的复杂处理。您现在可以对系统进行超过 20 秒的仿真。21 秒和 25 秒之间的状态震颤仍很大,软件在 20 秒左右发出警告。
使用 Second-Order Integrator 模块对弹球进行建模
sldemo_bounce 模型使用单个 Second-Order Integrator 模块对弹球进行建模。在本模型中,第二个方程  位于 Second-Order Integrator 模块的内部。打开 Second-Order Integrator 模块对话框,可以看到
位于 Second-Order Integrator 模块的内部。打开 Second-Order Integrator 模块对话框,可以看到  的下限为零。在属性选项卡上,选择
的下限为零。在属性选项卡上,选择 Reinitialize dx/dt when x reaches saturation。此参数允许您在  达到饱和界限时,将
达到饱和界限时,将  (弹球模型中的
(弹球模型中的  )重新初始化为新值。因此,对于弹球模型,当球触地时,其速度可以设置为不同值,例如撞击后的速度。请注意计算与地面碰撞后速度的循环。为了捕获即将触地之前球的速度
)重新初始化为新值。因此,对于弹球模型,当球触地时,其速度可以设置为不同值,例如撞击后的速度。请注意计算与地面碰撞后速度的循环。为了捕获即将触地之前球的速度 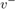 ,使用 Second-Order Integrator 模块的
,使用 Second-Order Integrator 模块的  输出端口和 Memory 模块。然后使用
输出端口和 Memory 模块。然后使用 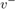 计算回弹速度
计算回弹速度  。
。


在“配置参数”对话框中,转至求解器窗格。
在仿真时间中,将停止时间设置为
25。展开求解器详细信息。在过零选项中,将算法设置为
Nonadaptive。
对模型进行仿真。
请注意,仿真没有遇到任何问题。在 20 秒后,您可以对模型进行仿真而不会出现过多震颤,同时无需将算法设置为 Adaptive。
比较弹球的建模方法
通过将每次弹跳所需的时间相加,您可以分析计算出球以零速度落地的准确时间 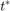 。此时间是由下式给出的无穷等比数列的总和:
。此时间是由下式给出的无穷等比数列的总和:

其中 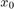 和
和 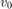 分别是位置和速度的初始条件。对于
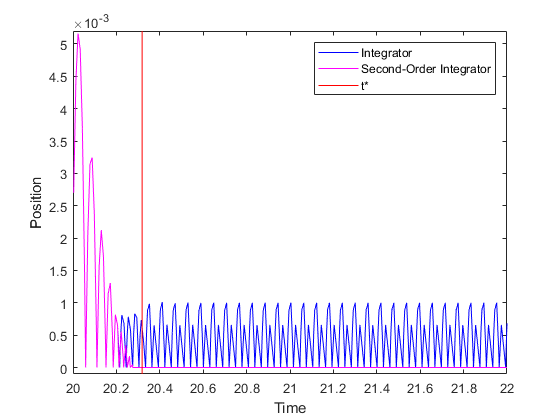
分别是位置和速度的初始条件。对于  ,球的速度和位置必须相同,都为零。该图显示
,球的速度和位置必须相同,都为零。该图显示 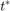 附近两次仿真的结果。图中的红色竖线是给定模型参数对应的
附近两次仿真的结果。图中的红色竖线是给定模型参数对应的 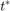 。如果
。如果 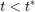 且远离
且远离 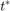 ,则这两个模型将生成准确且相同的结果。在绘图中只能看到来自第二个模型的品红色线。然而,第一个模型的仿真结果在
,则这两个模型将生成准确且相同的结果。在绘图中只能看到来自第二个模型的品红色线。然而,第一个模型的仿真结果在 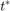 后并不精确。对于
后并不精确。对于  ,该图继续显示过多的震颤行为。相反,使用 Second-Order Integrator 模块的模型在
,该图继续显示过多的震颤行为。相反,使用 Second-Order Integrator 模块的模型在  精确稳定为零。
精确稳定为零。
与第一个模型相比,使用 Second-Order Integrator 模块的模型具有更好的数值特征,因为第二个微分方程  在 Second-Order Integrator 模块内部。模块算法可以利用这两种状态之间的关系,并使用启发式方法来抑制某些条件下的震颤行为。当两种状态由于积分误差和震颤行为而不再一致时,这些启发式方法变为活动状态。因此,您可以使用系统的物理知识来防止某些类型的 Zeno 模型的仿真陷入 Zeno 状态。
在 Second-Order Integrator 模块内部。模块算法可以利用这两种状态之间的关系,并使用启发式方法来抑制某些条件下的震颤行为。当两种状态由于积分误差和震颤行为而不再一致时,这些启发式方法变为活动状态。因此,您可以使用系统的物理知识来防止某些类型的 Zeno 模型的仿真陷入 Zeno 状态。
另请参阅
Integrator | Second-Order Integrator | Memory