代数环概念
当模型中的信号环仅包含具有直接馈通的模块时,将出现代数环。直接馈通是指模块使用当前时间步的输入值来计算当前时间步的输出值。仅包含具有直接馈通的模块的信号环会在同一时间步内产生模块输出和输入值的循环依赖关系。生成的方程是一个在每个时间步都需要求解的代数方程,这就增加了计算成本。
有些模块始终具有直接馈通,而其他模块仅在某些模块配置中具有直接馈通。具有直接馈通的模块的示例包括:
具有非零 D 矩阵的 State-Space 模块
分子阶数与分母阶数相同的 Transfer Fcn 模块
具有相同数量的零极点的 Zero-Pole 模块
没有直接馈通的模块保持一个或多个状态变量,这些变量存储来自先前时间步的输入值。没有直接馈通的模块示例包括 Integrator 模块和 Unit Delay 模块。
提示
要确定模块是否有直接馈通,请参考模块参考页上的模块特性表。要查看所有模块的模块特征,请使用 Block Support Table 模块或 showblockdatatypetable 函数。
假定有一个包含 Sum 模块的模型,该模块从输入值 u 中减去模块输出值 xa。

此模型实现以下方程
xa = u – xa.
对于此简单的循环,解是 xa = u/2。
数学解释
该软件包含几个可用于对常微分方程 (ODE) 进行仿真的数值求解器。ODE 是可以写为如下形式的方程组
其中 x 是状态向量,t 是时间自变量。
某些方程组包含涉及自变量和状态向量,但不涉及状态向量的导数的其他约束。此类方程组称为微分代数方程 (DAE)。
代数一词是指不涉及任何导数的方程。您可以用半显式格式来表示工程中出现的 DAE
其中:
f 和 g 可以是向量函数。
第一个方程是微分方程。
第二个方程是代数方程。
微分变量的向量是 x。
代数变量的向量是 xa。
在模型中,代数环表示代数约束。具有代数环的模型定义微分代数方程组。在使用 ODE 求解器的仿真的每一步,软件都会对 xa 的代数环进行数值求解。
假设有一个实现简单的 DAE 方程组的模型。内环表示代数约束,而外环表示微分方程。

此模型实现以下 DAE 方程组。
x' = xa
0 = u - x - 2xa
对于 ODE 求解器采用的每个步长,代数环求解器必须先求解代数约束的 xa,然后再计算导数 x'。
物理解释
代数约束:
在对物理系统建模时发生,通常是守恒定律所致,例如质量与能量守恒
当您为模型选择特定坐标系时发生
对动态系统中的系统响应的设计进行约束
使用 Simscape™ 将跨越机械、电气、液压和其他物理领域的系统建模为物理网络。Simscape 构造描述模型行为的 DAE。软件将这些方程与模型的其余部分集成,然后直接解算 DAE。Simulink® 同时对不同物理领域中的组件变量求解,从而避免代数环问题。
人为代数环
当原子子系统或 Model 模块导致 Simulink 检测到代数环时,将发生人为代数环,即使该子系统的内容不包含从输入到输出的直接馈通也是如此。当您创建原子子系统时,所有 Inport 模块都将是直接馈通,从而导致代数环。
以包含的模型为例,该模型表示被控对象的简单比例控制,其描述如下
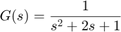
它可以重写为以下状态空间形式:
![$$ \dot{x} = \left[ \begin{array}{cc} -2 & -1 \\ 1 & 0 \end{array} \right] + \left( \begin{array}{c} 0\\1 \end{array} \right) $$](../../examples/simulink/win64/ArtifAlgLoopsExample_eq12603750421915334129.png)
![$$ y = \left[\begin{array}{cc}0&1\end{array}\right] $$](../../examples/simulink/win64/ArtifAlgLoopsExample_eq18346827941344727566.png)
该方程组既没有代数变量也没有直接馈通,因此不包含代数环。
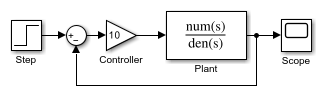
按照以下步骤中的说明修改模型:
将 Controller 和 Plant 模块包含在子系统中。
在子系统对话框中,选择视为原子单元使子系统成为原子子系统。
在模型配置参数的诊断窗格中,将代数环参数设置为
error。

在对此模型进行仿真时,会出现代数环,因为该子系统是直接馈通,即使原子子系统内的路径不是直接馈通也是如此。仿真停止并出现代数环错误。
代数环求解器的工作原理
当模型中包含代数环时,Simulink 在每个时间步使用非线性求解器解算代数环。求解器执行迭代以确定代数约束的解(如果存在)。因此,有代数环的模型的运行速度可能比没有代数环的模型的运行速度慢。
Simulink 使用折线信赖域算法解算代数环。使用的容差小于 ODE 求解器 Reltol 和 Abstol。这是因为 Simulink 使用“显式 ODE 方法”来解算指数为 1 的微分代数方程 (DAE)。
要使代数环求解器发挥作用,
必须存在一个模块,在该模块中,代数环求解器可以中断循环并尝试解算该循环。
模型应该具有双精度实信号。
基础代数约束必须是一个平滑函数。
例如,假设您的模型中有一个带两个输入的 Sum 模块:一个相加,另一个相减。如果您将 Sum 模块的输出馈送给其中一个输入,则会创建一个代数环,其中的所有模块都包括直接馈通。

Sum 模块无法在不知道输入的情况下计算输出。Simulink 会检测代数环,代数环求解器将使用迭代循环解算代数环。在 Sum 模块示例中,该软件通过以下方式计算正确的结果:
| xa(t) = u(t) /2. | (1) |
代数环求解器使用基于梯度的搜索方法,这需要与代数环相对应的代数约束的连续一阶导数。因此,如果代数环包含不连续性,代数环求解器可能会失败。
有关详细信息,请参阅 Solving Index-1 DAEs in MATLAB and Simulink(在 MATLAB 和 Simulink 中解算指数为 1 的 DAE) 1
代数环求解器中的信赖域算法和行搜索算法
Simulink 代数环求解器使用下面两种算法之一来解算代数环:
信赖域
行搜索
默认情况下,Simulink 选择最佳代数环求解器,并可能在仿真期间在两种方法之间切换。要为模型显式启用自动代数环求解器选项,请在 MATLAB® 命令行中输入:
set_param(model_name, 'AlgebraicLoopSolver','Auto');
要切换到信赖域算法,请在 MATLAB 命令行中,输入:
set_param(model_name, 'AlgebraicLoopSolver', 'TrustRegion');
如果代数环求解器不能解算使用信赖域算法的代数环,请尝试使用行搜索算法对模型进行仿真。
要切换到行搜索算法,请在 MATLAB 命令行中,输入:
set_param(model_name, 'AlgebraicLoopSolver', 'LineSearch');
有关详细信息,请参阅:
Shampine 和 Reichelt 的 nleqn.m 代码
User Guide for MINPACK-1(MINPACK-1 用户指南)中的 Fortran 程序 HYBRD12
Numerical Methods for Nonlinear Algebraic Equations(非线性代数方程的数值方法)中鲍威尔的“A Fortran subroutine for solving systems in nonlinear equations”(用于解算非线性系统的 Fortran 子例程)3
非线性最小化信赖域方法 (Optimization Toolbox).
线搜索 (Optimization Toolbox).
代数环求解器的限制
代数环解算是一个迭代过程。仅当代数环收敛到一个明确的答案时,Simulink 代数环求解器才会成功。当代数环无法收敛,或收敛速度太慢时,仿真将退出并显示错误。
代数环求解器无法解算包含以下任何一项的代数环:
带有离散值输出的模块
带有非双精度或复数输出的模块
不连续点
Stateflow® 图
模型中代数环的影响
如果您的模型包含代数环:
您不能为模型生成代码。
Simulink 代数环求解器可能无法解算代数环。
由于 Simulink 会尝试解算代数环,因此仿真执行速度可能很缓慢。
对于大多数模型,代数环求解器的第一个时间步会耗费大量计算资源。Simulink 能够快速解算后续时间步,因为上一个时间步为 xa 提供了良好的起点。
另请参阅
Algebraic Constraint | Descriptor State-Space
主题
1 Shampine, Lawrence F., M.W.Reichelt, and J.A.Kierzenka. ”Solving Index-1 DAEs in MATLAB and Simulink.”Siam Review.Vol.18,No.3,1999,pp.538–552.
2 More,J.J.,B.S.Garbow, and K.E.Hillstrom. User guide for MINPACK-1. Argonne, IL:Argonne National Laboratory,1980.
3 Rabinowitz, Philip, ed. Numerical Methods for Nonlinear Algebraic Equations, New York: Gordon and Breach Science Publishers, 1970.