Design Optimization to Meet a Custom Objective (Code)

Open Script

This example shows how to optimize a design to meet a custom objective using sdo.optimize. You optimize the cylinder parameters to minimize the cylinder geometry and satisfy design requirements.

Hydraulic Cylinder Model

Open the Simulink® model.

sys = 'sdoHydraulicCylinder';
open_system(sys);

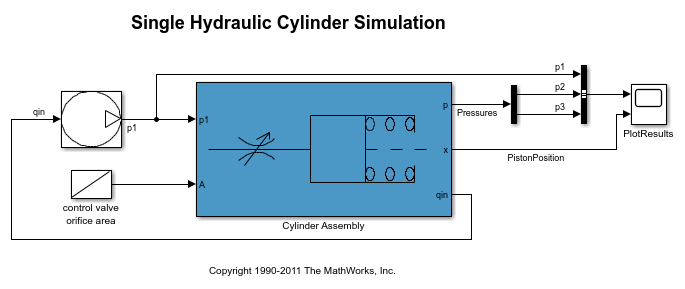
The hydraulic cylinder model is based on the Simulink model sldemo_hydcyl. The model includes:

Pump and Cylinder Assembly subsystems. For more information on the subsystems, see Single Hydraulic Cylinder Simulation.

A step change applied to the cylinder control valve orifice area that causes the cylinder piston position to change.

Hydraulic Cylinder Design Problem

You tune the cylinder cross-sectional area and piston spring constant to meet the following design requirements:

Ensure that the piston position has a step response rise time of less than 0.04 seconds and setting time of less than 0.05 seconds.

Limit the maximum cylinder pressures to 1.75e6 N/m.

Minimize the cylinder cross-sectional area.

Specify Design Variables

Select the following model parameters as design variables for optimization:

Cylinder cross-sectional area Ac

Piston spring constant K

Ac = sdo.getParameterFromModel('sdoHydraulicCylinder','Ac');
K  = sdo.getParameterFromModel('sdoHydraulicCylinder','K');

Limit the cylinder cross-sectional area to a circular area with radius between 1 and 2 centimeters.

Ac.Minimum = pi*1e-2^2; % m^2
Ac.Maximum = pi*2e-2^2; % m^2

Limit the piston spring constant to a range of 1e4 to 10e4 N/m.

K.Minimum  = 1e4;       % N/m
K.Maximum  = 10e4;      % N/m

Specify Design Requirements

The design requirements require logged model signals. During optimization, the model is simulated using the current value of the design variables and the logged signal is used to evaluate the design requirements.

Log the following signals:

Cylinder pressures, available at the first output port of the Cylinder Assembly block

Pressures = Simulink.SimulationData.SignalLoggingInfo;
Pressures.BlockPath       = 'sdoHydraulicCylinder/Cylinder Assembly';
Pressures.OutputPortIndex = 1;

Piston position, available at the second output port of the Cylinder Assembly block

PistonPosition = Simulink.SimulationData.SignalLoggingInfo;
PistonPosition.BlockPath       = 'sdoHydraulicCylinder/Cylinder Assembly';
PistonPosition.OutputPortIndex = 2;

Create an object to store the logging information and use later to simulate the model

simulator = sdo.SimulationTest('sdoHydraulicCylinder');
simulator.LoggingInfo.Signals = [PistonPosition,Pressures];

Specify the piston position step response requirement of rise time of less than 0.04 seconds and settling time less than of 0.05 seconds.

PistonResponse = sdo.requirements.StepResponseEnvelope;
set(PistonResponse, ...
    'RiseTime',        0.04, ...
    'FinalValue',      0.04, ...
    'SettlingTime',    0.05, ...
    'PercentSettling', 1);

Specify the maximum cylinder pressure requirement of less than 1.75e6 N/m.

MaxPressure = sdo.requirements.SignalBound;
set(MaxPressure, ...
    'BoundTimes',      [0 0.1], ...
    'BoundMagnitudes', [1.75e6 1.75e6], ...
    'Type',            '<=');

For convenience, collect the performance requirements into a single structure to use later.

requirements = struct(...
    'PistonResponse', PistonResponse, ...
    'MaxPressure',    MaxPressure);

Create Objective/Constraint Function

To optimize the cylinder cross-sectional area and piston spring constant, create a function to evaluate the cylinder design. This function is called at each optimization iteration.

Here, use an anonymous function with one argument that calls the sdoHydraulicCylinder_design function.

evalDesign = @(p) sdoHydraulicCylinder_design(p,simulator,requirements);

The function:

Has one input argument that specifies the cylinder cross-sectional area and piston spring constant values.

Returns the optimization objective value and optimization constraint violation values.

The optimization solver minimizes the objective value and attempts to keep the optimization constraint violation values negative. Type help sdoExampleCostFunction for more details on how to write the objective/constraint function.

The sdoHydraulicCylinder_design function uses the simulator and requirements objects to evaluate the design. Type edit sdoHydraulicCylinder_design to examine the function in more detail.

type sdoHydraulicCylinder_design

function design = sdoHydraulicCylinder_design(p,simulator,requirements)
%SDOHYDRAULICCYLINDER_DESIGN
%
% The sdoHydraulicCylinder_design function is used to evaluate a cylinder
% design.
%
% The |p| input argument is the vector of cylinder design parameters.
%
% The |simulator| input argument is a sdo.SimulinkTest object used to
% simulate the |sdoHydraulicCylinder| model and log simulation signals
%
% The |requirements| input argument contains the design requirements used
% to evaluate the cylinder design
%
% The |design| return argument contains information about the design
% evaluation that can be used by the |sdo.optimize| function to optimize
% the design.
%
% see also sdo.optimize, sdoExampleCostFunction

% Copyright 2011 The MathWorks, Inc.

%% Simulate the model
%
% Use the simulator input argument to simulate the model and log model
% signals.
% 
% First ensure that we simulate the model with the parameter values chosen
% by the optimizer.
%
simulator.Parameters = p;
% Simulate the model and log signals.
%
simulator = sim(simulator);
% Get the simulation signal log, the simulation log name is defined by the
% model |SignalLoggingName| property
%
logName = get_param('sdoHydraulicCylinder','SignalLoggingName');
simLog = get(simulator.LoggedData,logName);

%% Evaluate the design requirements
%
% Use the requirements input argument to evaluate the design requirements
%
% Check the PistonPosition signal against the stepresponse requirement
%
PistonPosition = get(simLog,'PistonPosition');
cPiston = evalRequirement(requirements.PistonResponse,PistonPosition.Values);
% Check the Pressure signals against the maximum requirement
%
Pressures = find(simLog,'Pressures');
cPressure = evalRequirement(requirements.MaxPressure,Pressures.Values);
% Use the PistonResponse and MaxPressure requirements as non-linear
% constraints for optimization.
design.Cleq = [cPiston(:);cPressure(:)];
% Add design objective to minimize the Cylinder cross-sectional area
Ac = p(1);          %Since we called sdo.optimize(evalDesign,[Ac;K])
design.F = Ac.Value;
end

Evaluate the Initial Design

Call the objective function with the initial cylinder cross-sectional area and initial piston spring constant.

initDesign = evalDesign([Ac;K]);

The function simulates the model and evaluates the design requirements. The scope shows that the maximum pressure requirement is satisfied but the piston position step response requirement is not satisfied.

initDesign is a structure with the following fields:

Cleq shows that some of the inequality constraints are positive indicating they are not satisfied by the initial design.

initDesign.Cleq

F shows the optimization objective value (in this case the cylinder cross-sectional area). The initial design cross-sectional area, as expected, has the same value as the initial cross-sectional area parameter Ac.

initDesign.F

ans =

   1.0000e-03

Optimize the Design

Pass the objective function, initial cross-sectional area and piston spring constant values to sdo.optimize.

[pOpt,optInfo] = sdo.optimize(evalDesign,[Ac;K]);

 Optimization started 2024-Sep-05, 19:04:21

                               max                     First-order 
 Iter F-count        f(x)   constraint    Step-size    optimality
    0      5        0.001       0.3033
    1     11   0.00057281      0.07293         0.48         43.2
    2     17  0.000391755            0        0.128         14.5
    3     22  0.000384694            0      0.00498      0.00615
    4     27  0.000379684            0      0.00362      0.00166
    5     32  0.000376044            0       0.0026      0.00023
Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.

The optimization repeatedly evaluates the cylinder design by adjusting the cross-sectional area and piston spring constant to meet the design requirements. From the scope, see that the maximum pressure and piston response requirements are met.

The sdo.optimize function returns:

pOpt shows the optimized cross-sectional area and piston spring constant values.

pOpt

 
pOpt(1,1) =
 
       Name: 'Ac'
      Value: 3.7604e-04
    Minimum: 3.1416e-04
    Maximum: 0.0013
       Free: 1
      Scale: 0.0020
       Info: [1x1 struct]

 
pOpt(2,1) =
 
       Name: 'K'
      Value: 1.5726e+04
    Minimum: 10000
    Maximum: 100000
       Free: 1
      Scale: 65536
       Info: [1x1 struct]

 
2x1 param.Continuous

optInfo is a structure that contains optimization termination information such as number of optimization iterations and the optimized design.

optInfo

optInfo = 

  struct with fields:

            Cleq: [10x1 double]
               F: 3.7604e-04
       Gradients: [1x1 struct]
        exitflag: 1
      iterations: 5
    SolverOutput: [1x1 struct]
           Stats: [1x1 struct]

For example, the Cleq field shows the optimized non-linear inequality constraints are all non-positive to within optimization tolerances, indicating that the maximum pressure and piston response requirements are satisfied.

optInfo.Cleq

ans =

   -0.0974
   -0.0135
   -0.0135
   -1.0000
   -0.2072
   -0.0044
   -0.0064
   -0.0004
   -0.0476
   -0.0476

The F field contains the optimized cross-sectional area. The optimized cross-sectional area value is nearly 50% less that the initial value.

optInfo.F

ans =

   3.7604e-04

Update the Model Variable Values

By default, the model variables Ac and K are not updated at the end of optimization. Use the setValueInModel command to update the model variable values.

sdo.setValueInModel('sdoHydraulicCylinder',pOpt)

Related Examples

To learn how to optimize the cylinder design using the Response Optimizer, see Design Optimization to Meet a Custom Objective (GUI).

% Close the model
bdclose('sdoHydraulicCylinder')