本页翻译不是最新的。点击此处可查看最新英文版本。

单液压缸仿真

打开模型

此示例说明如何使用 Simulink® 对液压缸进行建模。您可以将这些概念应用于需要液压行为建模的应用中。

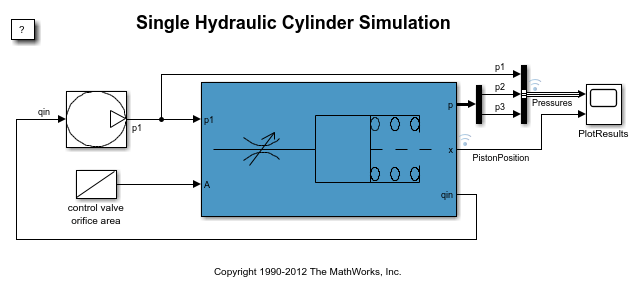
模型分析和物理学

此示意图显示液压缸的模型。该模型将泵流量 Q 引导至供应压力 p1，层流 q1ex 从供应压力泄漏至排气。活塞/缸组件的控制阀建模为通过可变面积孔口的紊流。其流量 q12 导致中间压力 p2，该压力随后在连接到作动器缸的管路中下降。缸压力 p3 克服弹簧负载移动活塞，从而产生位置 x。

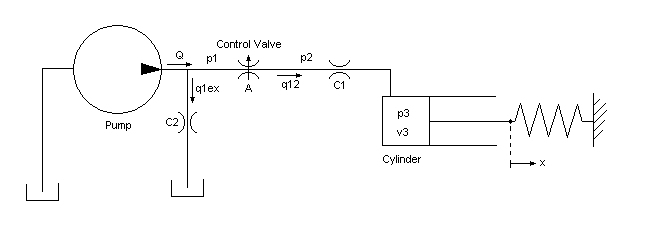
在泵输出端，流量分为泄漏流量和流向控制阀的流量。该模型使用方程组 1 方程将泄漏 q1ex 作为层流进行仿真。

方程组 1

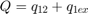
$$Q=q_{12}+q_{1ex}$$

$$q_{1ex}=C_2 \cdot p_1 $$

$$p_1=\frac{(Q-q_{12})}{C_2}$$

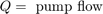
$$ Q = \mbox{ pump flow}$$

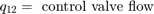
$$ q_{12} = \mbox{ control valve flow}$$

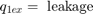
$$ q_{1ex} = \mbox{ leakage}$$

$$ C_2 = \mbox{ flow coefficient}$$

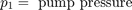
$$ p_1 = \mbox{ pump pressure}$$

该模型实现孔口方程以对通过控制阀的紊流进行仿真。符号函数和绝对值函数适用于任一方向的流量，如方程组 2 中所示。

方程组 2

$$q_{12}=C_d \cdot A \cdot sgn(p_1-p_2) \cdot \sqrt{\frac{2}{\rho}|p_1-p_2|}$$

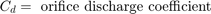
$$ C_d = \mbox{ orifice discharge coefficient} $$

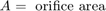
$$ A = \mbox{ orifice area} $$

$$ p_2 = \mbox{ pressure downstream of control valve} $$

$$ \rho = \mbox{ fluid density} $$

流体流 q12 = q23 减去活塞运动的柔度使得缸内的流体增压。该模型使用方程组 3 方程实现流体流和流可压缩性。

方程组 3

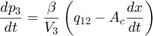
$$\frac{dp_3}{dt}=\frac{\beta}{V_3} \left(q_{12}-A_c \frac{dx}{dt}\right)$$

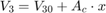
$$V_3=V_{30} + A_c \cdot x$$

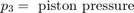
$$ p_3 = \mbox{ piston pressure} $$

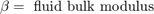
$$ \beta = \mbox{ fluid bulk modulus} $$

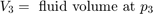
$$ V_3 = \mbox{ fluid volume at } p_3 $$

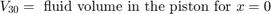
$$ V_{30}= \mbox{ fluid volume in the piston for } x = 0 $$

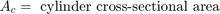
$$ A_c = \mbox{ cylinder cross-sectional area} $$

由于液压力较大，模型会忽略活塞和弹簧质量。通过对这种关系进行微分，并结合 p2 和 p3 之间的压降，将方程组纳入了模型中。

方程组 3 对从阀到作动器的层流进行建模。方程组 4 给出了活塞处的力平衡。

方程组 4

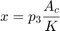
$$x=p_3\frac{A_c}{K}$$

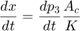
$$\frac{dx}{dt}=\frac{dp_3}{dt} \frac{A_c}{K}$$

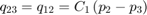
$$q_{23}=q_{12}=C_1 \left( p_2-p_3 \right)$$

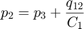
$$ p_2=p_3 + \frac{q_{12}}{C_1} $$

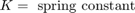
$$ K = \mbox{ spring constant} $$

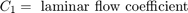
$$ C_1 = \mbox{ laminar flow coefficient} $$

运行仿真

要运行仿真，请在 Simulink 工具条上，点击运行。

在仿真期间，模型将相关数据记录到 MATLAB 工作区的 Simulink.SimulationOutput 对象 out 中。信号记录数据存储在 out 对象中名为 sldemo_hydcyl_output 的结构体中。记录的信号有蓝色标记。

Pump 子系统

要查看 Pump 子系统封装内部，请右键点击 Pump 子系统，然后选择封装 > 查看封装内部。泵模型将供应压力计算为泵流量和负载（输出）流量的函数。Qpump 是泵流量数据，保存在模型工作区中。包含时间点列向量和对应流速 [T,Q] 的矩阵指定流量数据。该模型计算压力 p1，如方程组 1 中所示。由于 Qout = q12 是 p1 的直接函数（通过控制阀），因此形成了一个代数环。对初始值的估计值 p10 可得到更高效的解。

您可以使用 Pump 子系统封装来访问和更改 T、Q、p10 和 C2 参数。

Valve/Cylinder/Piston/Spring Assembly 子系统

要查看 Actuator 子系统，请右键点击封装的 Valve/Cylinder/Piston/Spring Assembly 子系统，然后选择封装 > 查看封装内部。微分代数方程组用压力 p3 对缸增压进行建模，该压力在方程组 3 中显示为导数，并用作状态（积分器）。如果忽略活塞质量，则弹簧力和活塞位置直接是 p3 的倍数，速度直接是 p3 的时间导数的倍数。后一种关系形成围绕 Beta Gain 模块的代数环。中间压力 p2 是 p3 与从阀门流向缸的压降之和（参见方程组 4）。这种关系还通过控制阀和 1/C1 增益施加代数约束。

控制阀子系统计算孔口（参见方程组 2）。控制阀子系统使用上游和下游压力以及可变孔口面积作为输入。Control Valve Flow 子系统计算有符号平方根：

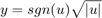
$$y=sgn(u)\sqrt{|u|}$$

该子系统实现三个非线性函数，其中两个是不连续的。然而，在组合中，y 是 u 的连续函数。

结果

模型仿真使用从 MAT 文件 sldemo_hydcyl_data.mat 加载的数据。您可以通过 Pump 和 Cylinder 封装更改参数值。

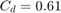
$$ C_d = 0.61 $$

$$ \rho = 800\,kg/m^3 $$

$$ C_1 = 2e-8\,m^3/sec/Pa $$

$$ C_2 = 3e-9\,m^3/sec/Pa $$

$$ \beta = 7e8\,Pa $$

$$ A_c = 1e-3\,m^2 $$

$$ K = 5e4\,N/m $$

$$ V_{30} = 2.5e-5\,m^3 $$

T = [0 0.04 0.04 0.05 0.05 0.1 ] sec

Q = [0.005 0.005 0 0 0.005 0.005] (m^3)/sec

绘制仿真结果

系统最初的泵流量为 0.005 m^3/sec = 300 l/min，在 t=0.04 sec 处降至零，然后在 t=0.05 sec 恢复为其初始流速。

控制阀从零孔口面积开始，在 0.1 秒的仿真时间内逐渐变为 1e-4 m^2。当阀门关闭时，所有泵流量都会泄漏，因此初始泵压增加到 p10 = Q/C2 = 1667 kPa。

当阀门打开时，压力 p2 和 p3 增加，而 p1 随着负载的增加而降低。当泵流量切断时，弹簧和活塞就像蓄能器一样工作，并且 p3 持续下降。然后流量反向流动，因此 p2（虽然相对接近 p3）却下降。在泵本身，所有回流均泄漏，并且 p1 下降。随着流量的还原，行为会发生逆转。

活塞位置与 p3 成正比，液压和弹簧力在此处保持平衡。在 0.04 秒和 0.05 秒处速度的不连续性表明质量可以忽略不计。当所有泵流量再次泄漏时，该模型达到稳定状态，这是由于现在控制阀上的压降为零，此时 p3 = p2 = p1 = p10。

另请参阅

主题