本页采用了机器翻译。点击此处可查看最新英文版本。

具有载荷约束的双缸模型

打开模型

此示例显示如何对支撑连接两个液压作动器的大质量的刚性杆进行建模。该模型消除了弹簧，因为它将活塞力直接施加于负载。这些力与重力平衡，导致线性和旋转位移。

模型分析和物理学

杆的旋转角度较小。下面的方程组 1 给出了杆的运动方程。描述气缸和泵行为的方程与单缸示例中的方程相同。

方程组 1：

$$M \frac{d^2 z}{d t^2} = F_b + F_a + F_{ext} $$

$$I \frac{d^2 \theta}{d t^2} = \frac{L}{2}F_b - \frac{L}{2}F_a $$

$$ z - \mbox{ displacement at the center } $$

$$ M - \mbox{ total mass } $$

$$ F_a - \mbox{ piston A force } $$

$$ F_b - \mbox{ piston B force } $$

$$ F_{ext} - \mbox{ external force at center } $$

$$ \theta - \mbox{ clockwise angular displacement } $$

$$ I - \mbox{ moment of inertia of the rod } $$

$$ L - \mbox{ rod length } $$

各个活塞的位置和速度直接取决于几何形状。参阅方程组 2 中的相应方程。

方程组 2：

$$ z_a = z - \theta \frac{L}{2} $$

$$ z_b = z + \theta \frac{L}{2} $$

$$ \frac{d z_a}{dt} = \frac{d z}{dt} - \frac{d \theta}{dt} \frac{L}{2} $$

$$ \frac{d z_b}{dt} = \frac{d z}{dt} + \frac{d \theta}{dt} \frac{L}{2} $$

$$ z_a - \mbox{ piston A displacement } $$

$$ z_b - \mbox{ piston B displacement } $$

开启并仿真模型

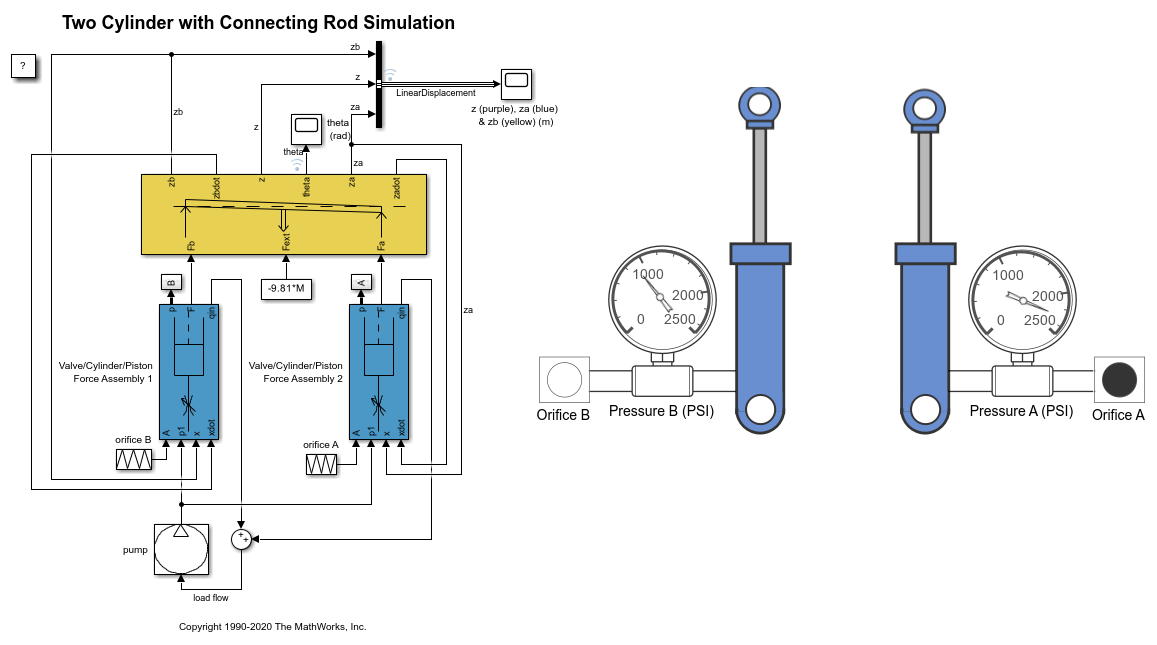
要打开此模型，请输入此命令：sldemo_hydrod。要运行仿真，请在仿真工具条上点击运行。模型：

  • 将信号数据记录到 Simulink.SimulationOutput 对象 out 中的 MATLAB® 工作区。信号记录数据存储在 out 中，在名为 sldemo_hydrod_output 的 Simulink.SimulationData.Dataset 对象中。

  • 将连续状态数据记录到 MATLAB 工作区。状态数据也包含在 out 工作区变量中，作为名为 xout 的结构。模型中每个状态都分配有一个名称，以帮助处理记录的数据。状态的名称可在 xout.signals 的 stateName 字段中找到。有关详细信息，请参阅记录的仿真数据的数据格式。

Mechanical Load 子系统

Mechanical Load 子系统解决运动方程，该方程直接使用标准 Simulink 模块计算。假设旋转角度很小。要查看 Mechanical Load 子系统的掩码下方及其结构，右键点击该子系统并选择封装 > 查看封装内部。

仿真参数

本次仿真中使用的参数与单液压缸仿真模型中使用的参数相同，但以下情况除外：

L     = 1.5 m
M     = 2500 kg
I     = 100 kg/m^2
Qmax = 0.005 m^3/sec (constant)
C2    = 3e-9 m^3/sec/Pa
Fext  = -9.81*M Newtons

尽管泵流量恒定，但模型可以独立控制阀门。最初，在 t = 0 处，阀门 B 的横截面为零。该值在 t = 0.01 sec 处线性增长到 1.2e-5 m^2，然后在 t = 0.02 sec 处线性减小到零。阀门 A 的横截面积为 1.2e-5 sq.m. 和 t = 0。该值在 t = 0.01 sec 处线性减小到零，然后在 t = 0.02 sec 处线性增加到 1.2e-5 sq.m。然后，阀门 A 和 B 的行为以相同的模式周期性地重复。换句话说，阀门 A 和 B 相差 180 度。

结果

这些图显示了杆的线性和角位移。线性位移响应是第一类积分系统的典型特征。杆的相对位置和角运动说明了两个活塞对异相控制信号的响应，或者阀门 A 和 B 的横截面。

另请参阅

|

主题