Gimbal Joint
Joint with three revolute primitives
Libraries:
Simscape /
Multibody /
Joints
Description
The Gimbal Joint block models a joint with three rotational degrees of freedom. The joint enables the follower frame to execute a 3-D rotation with respect to the base frame. The origins of the two frames are coincident. To achieve the 3-D rotation, the gimbal joint has three sequential rotations, as shown in the image.
The first rotation is about the x-axis of the follower frame, the second rotation is about the y-axis of the follower frame generated after the first rotation, and the third rotation is about the z-axis of the follower frame generated after the second rotation.
Gimbal joints have a kinematic singularity at configurations in which the second rotation is positive or negative 90 degrees. In these configurations, the first and third rotation axes are aligned and the joint loses a degree of freedom.
To specify the target of the initial state for a joint primitive, use the parameters under State Targets. The targets are specified in the base frame. You can also set the priority levels for the targets. If the joint is not able to satisfy all the state targets, the priority level determines which targets to satisfy first and how closely to satisfy them. For an example, see the Guiding Assembly section of How Multibody Assembly Works.
To model damping and the spring behavior for a joint primitive, use the parameters under Internal Mechanics. Use the Damping Coefficient parameter to model energy dissipation and the Spring Stiffness parameter to model energy storage. Joint springs attempt to displace the joint primitive from its equilibrium position, and joint dampers act as energy dissipation elements. The springs and dampers are strictly linear.
To specify the limits of a joint primitive, use the parameters under Limits. The lower and upper bounds define the width of the free region. The block applies a force to accelerate the joint position back to the free region when the position exceeds the bounds. The block uses a smoothed spring-damper method to compute the force. For more information about the smoothed spring-damper method, see the Description section of the Spatial Contact Force block.
The Force, Torque, and Motion parameters in the Actuation section control the motion of the joint primitives during simulation. For more information, see Specifying Joint Actuation Inputs. Additionally, the joint block has ports that output sensing data, such as position, velocity, acceleration, force, and torque, that you can use to perform analytical tasks on a model. For more information, see Sensing and Force and Torque Sensing.
To specify the joint mode configuration, use the Mode parameter. For more details, see Mode Configuration under the Ports and Parameters sections.
Examples
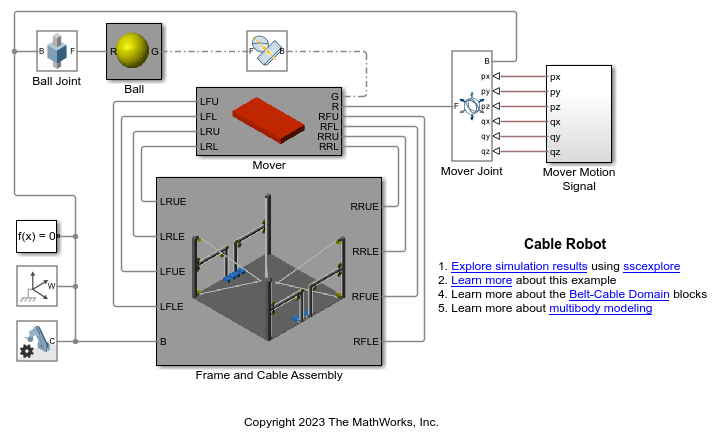
Cable Robot
Models a cable robot. The robot comprises 8 independent belt-cable circuits which control the 6 degrees-of-freedom of the mover. A ball is dropped from a fixed height down the center axis of the mechanism. The mover initially starts directly below the ball and the contact is modeled between the mover and the ball such that the ball bounces elastically when striking the mover. The objective of the mover is to perform increasingly complex maneuvers between successive bounces of the ball. The mover is motion actuated from which the necessary cable, pulley, and motor spool kinematics are computed.
Ports
Frame
B — Base frame
frame
Base frame of the joint block.
F — Follower frame
frame
Follower frame of the joint block.
Input
tx — Actuation torque
physical signal
Physical signal input port that accepts the actuation torque for the joint primitive. The block applies this torque equally and oppositely to both the base and follower frames of the joint primitive. The torque is about the x-axis of the base frame. The x-axes of the follower and base frames align with each other during simulation.
Dependencies
To enable this port, under X Revolute Primitive (Rx) > Actuation, set Torque to Provided by Input.
qx — Motion profile
physical signal
Physical signal input port that accepts the motion profile for the joint primitive. The block uses this signal to determine the rotation of the follower frame with respect to the base frame about the x-axis of the base frame. The signal must also contain the first and second derivatives of the rotation.
Dependencies
To enable this port, under X Revolute Primitive (Rx) > Actuation, set Motion to Provided by Input.
ty — Actuation torque
physical signal
Physical signal input port that accepts the actuation torque for the joint primitive. The block applies this torque equally and oppositely to both the base and follower frames of the joint primitive. The torque is about the y-axis of the base frame. The y-axes of the follower and base frames align with each other during simulation.
Dependencies
To enable this port, under Y Revolute Primitive (Ry) > Actuation, set Torque to Provided by Input.
qy — Motion profile
physical signal
Physical signal input port that accepts the motion profile for the joint primitive. The block uses this signal to determine the rotation of the follower frame with respect to the base frame about the y-axis of the base frame. The signal must also contain the first and second derivatives of the rotation.
Dependencies
To enable this port, under Y Revolute Primitive (Ry) > Actuation, set Motion to Provided by Input.
tz — Actuation torque
physical signal
Physical signal input port that accepts the actuation torque for the joint primitive. The block applies this torque equally and oppositely to both the base and follower frames of the joint primitive. The torque is about the z-axis of the base frame. The z-axes of the follower and base frames align with each other during simulation.
Dependencies
To enable this port, under Z Revolute Primitive (Rz) > Actuation, set Torque to Provided by Input.
qz — Motion profile
physical signal
Physical signal input port that accepts the motion profile for the joint primitive. The block uses this signal to determine the rotation of the follower frame with respect to the base frame about the z-axis of the base frame. The signal must also contain the first and second derivatives of the rotation.
Dependencies
To enable this port, under Z Revolute Primitive (Rz) > Actuation, set Motion to Provided by Input.
mode — Joint mode control
physical signal
Input port that controls the mode of the joint. The signal must be a unitless scalar. The
joint mode is normal when the input signal is 0, disengaged when
the input signal is -1, and locked when the input signal is
1. You can change the mode at any time during the
simulation.
The table shows how the position and velocity of the joint change during transitions between modes.
| Transitions | Position | Velocity |
|---|---|---|
| Normal to Locked | The joint position retains the current value and remains constant after the transition. | The joint velocity becomes zero and remains constant after the transition. |
| Normal to Disengaged | The joint position retains the current value but can change in any direction after the transition. | The joint velocity retains the current value but can change in any direction after the transition. |
| Locked to Normal | The joint position retains the current value but can change in the directions aligned with the joint degrees of freedom (DOFs) after the transition. | The joint velocity remains at zero but can change in the directions aligned with the joint DOFs after the transition. |
| Locked to Disengaged | The joint position retains the current value but can change in any direction after the transition. | The joint velocity remains at zero but can change in any direction after the transition. |
| Disengaged to Normal | For the directions aligned with the joint DOFs, the joint positions initially take values calculated by using Newton's method and can change thereafter. In the constrained directions, the joint positions become zero and remain constant after the transition. | For the directions aligned with the joint DOFs, the joint velocities initially take values calculated by using Newton's method and can change thereafter. In the constrained directions, the joint velocities become zero and remain constant after the transition. |
| Disengaged to Locked | For the directions aligned with the joint DOFs, the joint positions initially take values calculated by using Newton's method and remain constant after the transition. In the constrained directions, the joint positions become zero and remain constant after the transition. | The joint velocity becomes zero and remains constant after the transition. |
Dependencies
To enable this port, under Mode Configuration, set Mode to Provided by Input.
Output
qx — Position of joint primitive
physical signal
Physical signal port that outputs the position of the joint primitive. The value is the rotation angle of the follower frame with respect to the base frame about the x-axis of the base frame.
Dependencies
To enable this port, under X Revolute Primitive (Rx) > Sensing, select Position.
wx — Angular velocity of joint primitive
physical signal
Physical signal port that outputs the angular velocity of the joint primitive. The value is the first derivative of the signal from the port qx.
Dependencies
To enable this port, under X Revolute Primitive (Rx) > Sensing, select Velocity.
bx — Angular acceleration of joint primitive
physical signal
Physical signal port that outputs the angular acceleration of the joint primitive. The value is the second derivative of the signal from the port qx.
Dependencies
To enable this port, under X Revolute Primitive (Rx) > Sensing, select Acceleration.
tx — Actuator torque acting on joint primitive
physical signal
Physical signal port that outputs the actuator torque acting on the joint primitive.
Dependencies
To enable this port, under X Revolute Primitive (Rx) > Sensing, select Actuator Torque.
tllx — Lower-limit torque acting on joint primitive
physical signal
Physical signal port that outputs the lower-limit torque. The block applies this torque when the joint primitive position is less than the lower bound of the free region. The block applies this torque to both the base and follower frames of the joint primitive in order to accelerate the relative position back to the free region.
Dependencies
To enable this port, under X Revolute Primitive (Rx) > Sensing, select Lower-Limit Torque.
tulx — Upper-limit torque acting on joint primitive
physical signal
Physical signal port that outputs the upper-limit torque. The block applies this torque when the joint primitive position exceeds the upper bound of the free region. The block applies this torque to both the base and follower frames of the joint primitive in order to accelerate the relative position back to the free region.
Dependencies
To enable this port, under X Revolute Primitive (Rx) > Sensing, select Upper-Limit Torque.
qy — Position of joint primitive
physical signal
Physical signal port that outputs the position of the joint primitive. The value is the rotation angle of the follower frame with respect to the base frame about the y-axis of the base frame.
Dependencies
To enable this port, under Y Revolute Primitive (Ry) > Sensing, select Position.
wy — Angular velocity of joint primitive
physical signal
Physical signal port that outputs the angular velocity of the joint primitive. The value is the first derivative of the signal from the port qy.
Dependencies
To enable this port, under Y Revolute Primitive (Ry) > Sensing, select Velocity.
by — Angular acceleration of joint primitive
physical signal
Physical signal port that outputs the angular acceleration of the joint primitive. The value is the second derivative of the signal from the port qy.
Dependencies
To enable this port, under Y Revolute Primitive (Ry) > Sensing, select Acceleration.
ty — Actuator torque acting on joint primitive
physical signal
Physical signal port that outputs the actuator torque acting on the joint primitive.
Dependencies
To enable this port, under Y Revolute Primitive (Ry) > Sensing, select Actuator Torque.
tlly — Lower-limit torque acting on joint primitive
physical signal
Physical signal port that outputs the lower-limit torque. The block applies this torque when the joint primitive position is less than the lower bound of the free region. The block applies this torque to both the base and follower frames of the joint primitive in order to accelerate the relative position back to the free region.
Dependencies
To enable this port, under Y Revolute Primitive (Ry) > Sensing, select Lower-Limit Torque.
tuly — Upper-limit torque acting on joint primitive
physical signal
Physical signal port that outputs the upper-limit torque. The block applies this torque when the joint primitive position exceeds the upper bound of the free region. The block applies this torque to both the base and follower frames of the joint primitive in order to accelerate the relative position back to the free region.
Dependencies
To enable this port, under Y Revolute Primitive (Ry) > Sensing, select Upper-Limit Torque.
qz — Position of joint primitive
physical signal
Physical signal port that outputs the position of the joint primitive. The value is the rotation angle of the follower frame with respect to the base frame about the z-axis of the base frame.
Dependencies
To enable this port, under Z Revolute Primitive (Rz) > Sensing, select Position.
wz — Angular velocity of joint primitive
physical signal
Physical signal port that outputs the angular velocity of the joint primitive. The value is the first derivative of the signal from the port qz.
Dependencies
To enable this port, under Z Revolute Primitive (Rz) > Sensing, select Velocity.
bz — Angular acceleration of joint primitive
physical signal
Physical signal port that outputs the angular acceleration of the joint primitive. The value is the second derivative of the signal from the port qz.
Dependencies
To enable this port, under Z Revolute Primitive (Rz) > Sensing, select Acceleration.
tz — Actuator torque acting on joint primitive
physical signal
Physical signal port that outputs the actuator torque acting on the joint primitive.
Dependencies
To enable this port, under Z Revolute Primitive (Rz) > Sensing, select Actuator Torque.
tllz — Lower-limit torque acting on joint primitive
physical signal
Physical signal port that outputs the lower-limit torque. The block applies this torque when the joint primitive position is less than the lower bound of the free region. The block applies this torque to both the base and follower frames of the joint primitive in order to accelerate the relative position back to the free region.
Dependencies
To enable this port, under Z Revolute Primitive (Rz) > Sensing, select Lower-Limit Torque.
tulz — Upper-limit torque acting on joint primitive
physical signal
Physical signal port that outputs the upper-limit torque. The block applies this torque when the joint primitive position exceeds the upper bound of the free region. The block applies this torque to both the base and follower frames of the joint primitive in order to accelerate the relative position back to the free region.
Dependencies
To enable this port, under Z Revolute Primitive (Rz) > Sensing, select Upper-Limit Torque.
fc — Constraint force
physical signal
Physical signal port that outputs the constraint forces that act across the joint. The force maintains the translational constraints of the joint. For more information, see Measure Joint Constraint Forces.
Dependencies
To enable this port, under Composite Force/Torque Sensing, select Constraint Force.
tc — Constraint torque
physical signal
Physical signal port that outputs the constraint torques that act across the joint. The torque maintains the rotational constraints of the joint. For more information, see Force and Torque Sensing.
Dependencies
To enable this port, under Composite Force/Torque Sensing, select Constraint Torque.
ft — Total force
physical signal
Physical signal port that outputs the total force that acts across the joint. The total force is the sum of the forces transmitted from one frame to the other through the joint. The force includes the actuation, internal, limit, and constraint forces. See Force and Torque Sensing for more information.
Dependencies
To enable this port, under Composite Force/Torque Sensing, select Total Force.
tt — Total torque
physical signal
Physical signal port that outputs the total torque that acts across the joint. The total torque is the sum of the torques transmitted from one frame to the other through the joint. The torque includes the actuation, internal, limit, and constraint torques. For more information, see Force and Torque Sensing.
Dependencies
To enable this port, under Composite Force/Torque Sensing, select Total Torque.
Parameters
To edit block parameters interactively, use the Property Inspector. From the Simulink® Toolstrip, on the Simulation tab, in the Prepare gallery, select Property Inspector.
X Revolute Primitive (Rx)
State TargetsSpecify Position Target — Whether to specify position target
off (default) | on
Select this parameter to specify the position target of the x revolute primitive.
Priority — Priority level of position target
High (desired) (default) | Low (approximate)
Priority level of the position target, specified as High (desired)
or Low (approximate). For more information, see the
Guiding Assembly section of How Multibody Assembly Works..
Dependencies
To enable this parameter, select Specify Position Target.
Value — Position target
0 deg (default) | scalar
Position target of the x revolute primitive, specified as a scalar with a unit of angle.
Dependencies
To enable this parameter, select Specify Position Target.
Specify Velocity Target — Whether to specify angular velocity target
off (default) | on
Select this parameter to specify the angular velocity target for the x revolute primitive.
Priority — Priority level of velocity target
High (desired) (default) | Low (approximate)
Priority level of the angular velocity target, specified as High
(desired) or Low (approximate). For
more information, see the Guiding Assembly section of How Multibody Assembly Works.
Dependencies
To enable this parameter, select Specify Velocity Target.
Value — Velocity target
0 deg/s (default) | scalar
Angular velocity target of the x revolute primitive, specified as a scalar with a unit of angular velocity.
Dependencies
To enable this parameter, select Specify Velocity Target.
Equilibrium Position — Position where internal torque is zero
0 deg (default) | scalar
Position where the spring torque is zero, specified as a scalar with a unit of angle.
Spring Stiffness — Stiffness of force law
0 N*m/deg (default) | scalar
Stiffness of the internal spring-damper force law for the x revolute primitive, specified as a scalar with a unit of torsional stiffness.
Damping Coefficient — Damping coefficient of force law
0 N*m/(deg/s) (default) | scalar
Damping coefficient of the internal spring-damper force law for the x revolute primitive, specified as a scalar with a unit of damping coefficient.
Specify Lower Limit — Whether to specify lower position limit
off (default) | on
Select this parameter to specify the lower limit of the x revolute primitive.
Bound — Lower bound of free region
-90 deg (default) | scalar
Lower bound for the free region of the x revolute primitive, specified as a scalar with a unit of angle.
Dependencies
To enable this parameter, select Specify Lower Limit.
Spring Stiffness — Stiffness of spring at lower bound
1e4 N*m/deg (default) | scalar
Stiffness of the spring at the lower bound, specified as a scalar with a unit of torsional stiffness.
Dependencies
To enable this parameter, select Specify Lower Limit.
Damping Coefficient — Damping coefficient at lower bound
10 N*m/(deg/s) (default) | scalar
Damping coefficient at the lower bound, specified as a scalar with a unit of damping coefficient.
Dependencies
To enable this parameter, select Specify Lower Limit.
Transition Region Width — Region to smooth spring and damper torques
0.1 deg (default) | scalar
Region to smooth the spring and damper torques, specified as a scalar with a unit of angle.
The block applies the full value of the lower-limit torque when the penetration reaches the width of the transition region. The smaller the region, the sharper the onset of forces and the smaller the time step required of the solver. In the tradeoff between simulation accuracy and simulation speed, reducing the transition region improves accuracy and expanding it improves speed.
Dependencies
To enable this parameter, select Specify Lower Limit.
Specify Upper Limit — Whether to specify upper position limit
off (default) | on
Select this parameter to specify the upper limit of the x revolute primitive.
Bound — Upper bound of free region
90 deg (default) | scalar
Upper bound for the free region of the x revolute primitive, specified as a scalar with a unit of angle.
Dependencies
To enable this parameter, select Specify Upper Limit.
Spring Stiffness — Stiffness of spring at upper bound
1e4 N*m/deg (default) | scalar
Stiffness of the spring at the upper bound, specified as a scalar with a unit of torsional stiffness.
Dependencies
To enable this parameter, select Specify Upper Limit.
Damping Coefficient — Damping coefficient at upper bound
10 N*m/(deg/s) (default) | scalar
Damping coefficient at the upper bound, specified as a scalar with a unit of damping coefficient.
Dependencies
To enable this parameter, select Specify Upper Limit.
Transition Region Width — Region to smooth spring and damper torques
0.1 deg (default) | scalar
Region to smooth the spring and damper torques, specified as a scalar with a unit of angle.
The block applies the full value of the upper-limit torque when the penetration reaches the width of the transition region. The smaller the region, the sharper the onset of forces and the smaller the time step required of the solver. In the tradeoff between simulation accuracy and simulation speed, reducing the transition region improves accuracy and expanding it improves speed.
Dependencies
To enable this parameter, select Specify Upper Limit.
Torque — Option to provide actuator torque
None (default) | Provided by Input | Automatically Computed
Option to provide the actuator torque for the joint primitive, specified as one of these values:
| Torque Setting | Description |
|---|---|
None | No actuator torque. |
Provided by Input | The input port tx specifies the actuator torque for the x revolute primitive. |
Automatically Computed | The block computes the torque automatically. If you set this parameter to Automatically Computed, you do not need to set Motion to Provided by Input for the for the same joint primitive. The automatically computed torque may satisfy a motion input somewhere else in the mechanism. |
Motion — Option to provide motion
Automatically Computed (default) | Provided by Input
Option to provide the motion for the joint primitive, specified as one of these values:
| Motion Setting | Description |
|---|---|
Automatically computed | The block computes and applies the joint primitive motion based on model dynamics. |
Provided by Input | The input port qx specifies the motion for the x revolute primitive. |
Y Revolute Primitive (Ry)
State TargetsSpecify Position Target — Whether to specify position target
off (default) | on
Select this parameter to specify the position target of the y revolute primitive.
Priority — Priority level of position target
High (desired) (default) | Low (approximate)
Priority level of the position target, specified as High (desired)
or Low (approximate). For more information, see the
Guiding Assembly section of How Multibody Assembly Works.
Dependencies
To enable this parameter, select Specify Position Target.
Value — Position target
0 deg (default) | scalar
Position target of the y revolute primitive, specified as a scalar with a unit of angle.
Dependencies
To enable this parameter, select Specify Position Target.
Specify Velocity Target — Whether to specify angular velocity target
off (default) | on
Select this parameter to specify the angular velocity target for the y revolute primitive.
Priority — Priority level of velocity target
High (desired) (default) | Low (approximate)
Priority level of the angular velocity target, specified as High
(desired) or Low (approximate). For
more information, see the Guiding Assembly section of How Multibody Assembly Works.
Dependencies
To enable this parameter, select Specify Velocity Target.
Value — Velocity target
0 deg/s (default) | scalar
Angular velocity target of the y revolute primitive, specified as a scalar with a unit of angular velocity.
Dependencies
To enable this parameter, select Specify Velocity Target.
Equilibrium Position — Position where internal torque is zero
0 deg (default) | scalar
Position where the spring torque is zero, specified as a scalar with a unit of angle.
Spring Stiffness — Stiffness of force law
0 N*m/deg (default) | scalar
Stiffness of the internal spring-damper force law for the y revolute primitive, specified as a scalar with a unit of torsional stiffness.
Damping Coefficient — Damping coefficient of force law
0 N*m/(deg/s) (default) | scalar
Damping coefficient of the internal spring-damper force law for the y revolute primitive, specified as a scalar with a unit of damping coefficient.
Specify Lower Limit — Whether to specify lower position limit
off (default) | on
Select this parameter to specify the lower limit of the y revolute primitive.
Bound — Lower bound of free region
-90 deg (default) | scalar
Lower bound for the free region of the y revolute primitive, specified as a scalar with a unit of angle.
Dependencies
To enable this parameter, select Specify Lower Limit.
Spring Stiffness — Stiffness of spring at lower bound
1e4 N*m/deg (default) | scalar
Stiffness of the spring at the lower bound, specified as a scalar with a unit of torsional stiffness.
Dependencies
To enable this parameter, select Specify Lower Limit.
Damping Coefficient — Damping coefficient at lower bound
10 N*m/(deg/s) (default) | scalar
Damping coefficient at the lower bound, specified as a scalar with a unit of damping coefficient.
Dependencies
To enable this parameter, select Specify Lower Limit.
Transition Region Width — Region to smooth spring and damper torques
0.1 deg (default) | scalar
Region to smooth the spring and damper torques, specified as a scalar with a unit of angle.
The block applies the full value of the lower-limit torque when the penetration reaches the width of the transition region. The smaller the region, the sharper the onset of forces and the smaller the time step required of the solver. In the tradeoff between simulation accuracy and simulation speed, reducing the transition region improves accuracy and expanding it improves speed.
Dependencies
To enable this parameter, select Specify Lower Limit.
Specify Upper Limit — Whether to specify upper position limit
off (default) | on
Select this parameter to specify the upper limit of the y revolute primitive.
Bound — Upper bound of free region
90 deg (default) | scalar
Upper bound for the free region of the y revolute primitive, specified as a scalar with a unit of angle.
Dependencies
To enable this parameter, select Specify Upper Limit.
Spring Stiffness — Stiffness of spring at upper bound
1e4 N*m/deg (default) | scalar
Stiffness of the spring at the upper bound, specified as a scalar with a unit of torsional stiffness.
Dependencies
To enable this parameter, select Specify Upper Limit.
Damping Coefficient — Damping coefficient at upper bound
10 N*m/(deg/s) (default) | scalar
Damping coefficient at the upper bound, specified as a scalar with a unit of damping coefficient.
Dependencies
To enable this parameter, select Specify Upper Limit.
Transition Region Width — Region to smooth spring and damper torques
0.1 deg (default) | scalar
Region to smooth the spring and damper torques, specified as a scalar with a unit of angle.
The block applies the full value of the upper-limit torque when the penetration reaches the width of the transition region. The smaller the region, the sharper the onset of forces and the smaller the time step required of the solver. In the tradeoff between simulation accuracy and simulation speed, reducing the transition region improves accuracy and expanding it improves speed.
Dependencies
To enable this parameter, select Specify Upper Limit.
Torque — Option to provide actuator torque
None (default) | Provided by Input | Automatically Computed
Option to provide the actuator torque for the joint primitive, specified as one of these values:
| Torque Setting | Description |
|---|---|
None | No actuator torque. |
Provided by Input | The input port ty specifies the actuator torque for the y revolute primitive. |
Automatically Computed | The block computes the torque automatically. If you set this parameter to Automatically Computed, you do not need to set Motion to Provided by Input for the for the same joint primitive. The automatically computed torque may satisfy a motion input somewhere else in the mechanism. |
Motion — Option to provide motion
Automatically Computed (default) | Provided by Input
Option to provide the motion for the joint primitive, specified as one of these values:
| Motion Setting | Description |
|---|---|
Automatically computed | The block computes and applies the joint primitive motion based on model dynamics. |
Provided by Input | The input port qy specifies the motion for the y revolute primitive. |
Z Revolute Primitive (Rz)
State TargetsSpecify Position Target — Whether to specify position target
off (default) | on
Select this parameter to specify the position target of the z revolute primitive.
Priority — Priority level of position target
High (desired) (default) | Low (approximate)
Priority level of the position target, specified as High
(desired) or Low (approximate). For
more information, see the Guiding Assembly section of How Multibody Assembly Works.
Dependencies
To enable this parameter, select Specify Position Target.
Value — Position target
0 deg (default) | scalar
Position target of the z revolute primitive, specified as a scalar with a unit of angle.
Dependencies
To enable this parameter, select Specify Position Target.
Specify Velocity Target — Whether to specify angular velocity target
off (default) | on
Select this parameter to specify the angular velocity target for the z revolute primitive.
Priority — Priority level of velocity target
High (desired) (default) | Low (approximate)
Priority level of the angular velocity target, specified as High
(desired) or Low (approximate). For
more information, see the Guiding Assembly section of How Multibody Assembly Works.
Dependencies
To enable this parameter, select Specify Velocity Target.
Value — Velocity target
0 deg/s (default) | scalar
Angular velocity target of the z revolute primitive, specified as a scalar with a unit of angular velocity.
Dependencies
To enable this parameter, select Specify Velocity Target.
Equilibrium Position — Position where internal torque is zero
0 deg (default) | scalar
Position where the spring torque is zero, specified as a scalar with a unit of angle.
Spring Stiffness — Stiffness of force law
0 N*m/deg (default) | scalar
Stiffness of the internal spring-damper force law for the z revolute primitive, specified as a scalar with a unit of torsional stiffness.
Damping Coefficient — Damping coefficient of force law
0 N*m/(deg/s) (default) | scalar
Damping coefficient of the internal spring-damper force law for the z revolute primitive, specified as a scalar with a unit of damping coefficient.
Specify Lower Limit — Whether to specify lower position limit
off (default) | on
Select this parameter to specify the lower limit of the z revolute primitive.
Bound — Lower bound of free region
-90 deg (default) | scalar
Lower bound for the free region of the z revolute primitive, specified as a scalar with a unit of angle.
Dependencies
To enable this parameter, select Specify Lower Limit.
Spring Stiffness — Stiffness of spring at lower bound
1e4 N*m/deg (default) | scalar
Stiffness of the spring at the lower bound, specified as a scalar with a unit of torsional stiffness.
Dependencies
To enable this parameter, select Specify Lower Limit.
Damping Coefficient — Damping coefficient at lower bound
10 N*m/(deg/s) (default) | scalar
Damping coefficient at the lower bound, specified as a scalar with a unit of damping coefficient.
Dependencies
To enable this parameter, select Specify Lower Limit.
Transition Region Width — Region to smooth spring and damper torques
0.1 deg (default) | scalar
Region to smooth the spring and damper torques, specified as a scalar with a unit of angle.
The block applies the full value of the lower-limit torque when the penetration reaches the width of the transition region. The smaller the region, the sharper the onset of forces and the smaller the time step required of the solver. In the tradeoff between simulation accuracy and simulation speed, reducing the transition region improves accuracy and expanding it improves speed.
Dependencies
To enable this parameter, select Specify Lower Limit.
Specify Upper Limit — Whether to specify upper position limit
off (default) | on
Select this parameter to specify the upper limit of the z revolute primitive.
Bound — Upper bound of free region
90 deg (default) | scalar
Upper bound for the free region of the z revolute primitive, specified as a scalar with a unit of angle.
Dependencies
To enable this parameter, select Specify Upper Limit.
Spring Stiffness — Stiffness of spring at upper bound
1e4 N*m/deg (default) | scalar
Stiffness of the spring at the upper bound, specified as a scalar with a unit of torsional stiffness.
Dependencies
To enable this parameter, select Specify Upper Limit.
Damping Coefficient — Damping coefficient at upper bound
10 N*m/(deg/s) (default) | scalar
Damping coefficient at the upper bound, specified as a scalar with a unit of damping coefficient.
Dependencies
To enable this parameter, select Specify Upper Limit.
Transition Region Width — Region to smooth spring and damper torques
0.1 deg (default) | scalar
Region to smooth the spring and damper torques, specified as a scalar with a unit of angle.
The block applies the full value of the upper-limit torque when the penetration reaches the width of the transition region. The smaller the region, the sharper the onset of forces and the smaller the time step required of the solver. In the tradeoff between simulation accuracy and simulation speed, reducing the transition region improves accuracy and expanding it improves speed.
Dependencies
To enable this parameter, select Specify Upper Limit.
Torque — Option to provide actuator torque
None (default) | Provided by Input | Automatically Computed
Option to provide the actuator torque for the joint primitive, specified as one of these values:
| Torque Setting | Description |
|---|---|
None | No actuator torque. |
Provided by Input | The input port tz specifies the actuator torque for the z revolute primitive. |
Automatically Computed | The block computes the torque automatically. If you set this
parameter to Automatically Computed,
you do not need to set Motion to
Provided by Input for the for
the same joint primitive. The automatically computed torque may
satisfy a motion input somewhere else in the mechanism. |
Motion — Option to provide motion
Automatically Computed (default) | Provided by Input
Option to provide the motion for the joint primitive, specified as one of these values:
| Motion Setting | Description |
|---|---|
Automatically computed | The block computes and applies the joint primitive motion based on model dynamics. |
Provided by Input | The input port qz specifies the motion for the z revolute primitive. |
Mode Configuration
Mode — Joint mode
Normal (default) | Locked | Disengaged | Provided by Input
Joint mode for the simulation, specified as one of these values:
| Mode | Description |
|---|---|
Locked | Locked mode constrains all the degrees of freedom (DOFs) for the joint. The locked joint maintains its initial assembly position with zero velocity during the simulation. The joint block can sense forces or torques in accordance with the settings of the Internal Mechanics, Limits, and Actuation parameters. |
Normal | Normal mode enables the DOFs and the constraints of the joint work as intended during the simulation. |
Disengaged | Disengaged mode releases the joint from all constraints throughout the simulation. The settings for Internal Mechanics, Limits, and Actuation parameters do not affect the disengaged joint. All output ports output zero. |
Provided by Input | The Provided by Input option allows you to specify the joint mode
by using an input signal. For more information, see the port
mode in the Input
section. |
Composite Force/Torque Sensing
Direction — Measurement direction
Follower on Base (default) | Base on Follower
Measurement direction, specified as one of these values:
Follower on Base— The block senses the force and torque that the follower frame exerts on the base frame.Base on Follower— The block senses the force and torque that the base frame exerts on the follower frame.
This parameter affects only the output signals under the Composite Force/Torque Sensing section. Reversing the direction changes the sign of the measurements. For more information, see Force and Torque Measurement Direction.
Resolution Frame — Frame used to resolve measurements
Base (default) | Follower
Frame used to resolve the measurements, specified as one of these values:
Base— The block resolves the measurements in the coordinates of the base frame.Follower— The block resolves the measurements in the coordinates of the follower frame.
This parameter affects only the output signals under the Composite Force/Torque Sensing section.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
Version History
Introduced in R2012a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)
Asia Pacific
- Australia (English)
- India (English)
- New Zealand (English)
- 中国
- 日本Japanese (日本語)
- 한국Korean (한국어)