Battery

Behavioral battery model

Libraries:
Simscape / Electrical / Sources
Simscape / Battery / Cells

Description

The Battery block represents a simple battery model. You can also expose the charge output port and the thermal port of the battery.

To measure the internal charge level of the battery, in the Main section, set the Expose charge measurement port to Yes. This action exposes an extra physical signal port that outputs the internal state of charge. Use this functionality to change load behavior as a function of state of charge, without the complexity of building a charge state estimator.

To simulate the thermal effects of the battery, in the Thermal Port section, set the Thermal port parameter to Model. This action exposes an extra thermal port, which represents the battery thermal mass. When you select this option, provide additional parameters to define battery behavior at a second temperature. For more information, see Modeling Thermal Effects.

The battery equivalent circuit is made up of the fundamental battery model, the self-discharge resistance R_SD, the charge dynamics model, and the series resistance R₀.

Battery Model

If you select Infinite for the Battery charge capacity parameter, the block models the battery as a series resistor and a constant voltage source. If you select Finite for the Battery charge capacity parameter, the block models the battery as a series resistor and a charge-dependent voltage source. In the finite case, the voltage is a function of charge and has the following relationship:

$V = V_{0} (\frac{SOC}{1 - β (1 - SOC)})$

where:

SOC (state-of-charge) is the ratio of current charge to rated battery capacity.
V₀ is the voltage when the battery is fully charged at no load, as defined by the Nominal voltage, Vnom parameter.
β is a constant that is calculated so that the battery voltage is V1 when the charge is AH1. Specify the voltage V1 and cell capacityAH1 using block parameters. AH1 is the charge when the no-load (open-circuit) voltage is V1, and V1 is less than the nominal voltage.

The equation defines an approximate relationship between voltage and remaining charge. This approximation replicates the increasing rate of voltage drop at low charge values, and ensures that the battery voltage becomes zero when the charge level is zero. The advantage of this model is that it requires few parameters, which are readily available on most datasheets.

Modeling Battery Fade

For battery models with finite battery charge capacity, you can model battery performance deterioration depending on the number of discharge cycles. This deterioration is referred to as battery fade. To enable battery fade, set the Battery fade parameter to Enabled. This setting exposes additional parameters in the Fade section.

The block implements battery fade by scaling certain battery parameter values that you specify in the Main section, depending on the number of completed discharge cycles. The block uses multipliers λ_AH, λ_R0, and λ_V1 on the Cell capacity (Ah rating), Internal resistance, and Voltage V1 when charge is AH1 parameter values, respectively. These multipliers, in turn, depend on the number of discharge cycles:

$λ_{A H} = 1 - k_{1} N^{0.5}$

$λ_{R 0} = 1 + k_{2} N^{0.5}$

$λ_{V 1} = 1 - k_{3} N$

$N = N_{0} + \frac{1}{A H} \int_{0}^{t} \frac{i (t) \cdot H (i (t))}{λ_{A H} (t)} d t$

where:

λ_AH is the multiplier for battery nominal capacity.
λ_R0 is the multiplier for battery series resistance.
λ_V1 is the multiplier for voltage V1.
N is the number of discharge cycles completed.
N₀ is the number of full discharge cycles completed before the start of the simulation.
AH is the rated battery capacity in ampere-hours.
i(t) is the instantaneous battery output current.
H(i(t)) is the Heaviside function of the instantaneous battery output current. This function returns 0 if the argument is negative, and 1 if the argument is positive.

Note

The Battery block tracks the current and integrates it over time. The number of discharge cycles completed N increases by 1 every time an equivalent cell discharge capacity is extracted.

The block calculates the coefficients k₁, k₂, and k₃ by substituting the parameter values you provide in the Fade section into these battery equations. For example, the default set of block parameters corresponds to the following coefficient values:

k₁ = 1e-2
k₂ = 1e-3
k₃ = 1e-3

You can also define a starting point for a simulation based on the previous charge-discharge history by using the high-priority variable Discharge cycles. For more information, see Variables.

Modeling Thermal Effects

If you set the Thermal port parameter to Model, you must provide additional parameters to define battery behavior at a second temperature. The extended equations for the voltage when you expose the thermal port are:

$V = V_{0 T} (\frac{SOC}{1 - β_{T} (1 - SOC)})$

$V_{0 T} = V_{0} (1 + λ_{V} (T - T_{1}))$

where:

T is the battery temperature.
T₁ is the nominal measurement temperature.
λ_V is the parameter temperature dependence coefficient for V₀.
$β_{T} = β [1 + λ_{β} (T - T_{1})] .$
λ_β is the parameter temperature dependence coefficient for β.
β is calculated in the same way as Battery Model, using the temperature-modified nominal voltage V_0T.

The internal series resistance, self-discharge resistance, and any charge-dynamic resistances are also functions of temperature:

$R_{T} = R (1 + λ_{R} (T - T_{1}))$

where λ_R is the parameter temperature dependence coefficient.

All the temperature dependence coefficients are determined from the corresponding values you provide at the nominal and second measurement temperatures. If you include charge dynamics in the model, the time constants vary with temperature in the same way.

The battery temperature is determined from a summation of all the ohmic losses included in the model:

$M_{t h} \dot{T} = \sum_{i} V_{T, i}^{2} / R_{T, i}$

where:

M_th is the battery thermal mass.
i corresponds to the ith ohmic loss contributor. Depending on how you have configured the block, the losses include:
- Series resistance
- Self-discharge resistance
- First charge dynamics segment
- Second charge dynamics segment
- Third charge dynamics segment
- Fourth charge dynamics segment
- Fifth charge dynamics segment
V_T,i is the voltage drop across resistor i.
R_T,i is resistor i.

Modeling Charge Dynamics

You can model battery charge dynamics by using the Charge dynamics parameter:

No dynamics — The equivalent circuit contains no parallel RC sections. There is no delay between terminal voltage and internal charging voltage of the battery.
One time-constant dynamics — The equivalent circuit contains one parallel RC section. Specify the time constant using the First time constant parameter.
Two time-constant dynamics — The equivalent circuit contains two parallel RC sections. Specify the time constants using the First time constant and Second time constant parameters.
Three time-constant dynamics — The equivalent circuit contains three parallel RC sections. Specify the time constants using the First time constant, Second time constant, and Third time constant parameters.
Four time-constant dynamics — The equivalent circuit contains four parallel RC sections. Specify the time constants using the First time constant, Second time constant, Third time constant, and Fourth time constant parameters.
Five time-constant dynamics — The equivalent circuit contains five parallel RC sections. Specify the time constants using the First time constant, Second time constant, Third time constant, Fourth time constant, and Fifth time constant parameters.

This figure shows the equivalent circuit for the block configured with two time-constant dynamics.

In the diagram:

R_RC1 and R_RC2 are the parallel RC resistances. Specify these values with the First polarization resistance and Second polarization resistance parameters, respectively.
C_RC1 and C_RC2 are the parallel RC capacitances. The time constant τ for each parallel section relates the R and C values using the relationship $C = τ / R$ . Specify τ for each section using the First time constant and Second time constant parameters, respectively.
R₀ is the series resistance. Specify this value with the Internal resistance parameter.

Modeling Battery Aging

For battery models with finite battery charge capacity, you can model the battery performance deterioration that occurs when the battery is not used. Calendar aging affects both the internal resistance and capacity. In particular, the resistance increase depends by various mechanisms such as the creation of Solid Electrolyte Interface (SEI) at both anode and cathode and the corrosion of the current collector. These processes mainly depend on the storage temperature, the storage state of charge, and time.

Note

The Battery block only applies the calendar aging during initialization. When you set the Calendar aging parameter to Enabled, the block exposes the Vector of time intervals parameter that represents the time the battery has aged before the start of the simulation. Calendar aging during the simulation is not covered with this option.

This equation defines the terminal resistance increase of the battery due to calendar aging:

$\begin{matrix} α_{r} (T, V_{o c}) = (b V_{o c} - c) e^{- \frac{q d}{k T}}, \\ R = R_{0} (1 + \sum_{i = 1}^{i = n} α_{r} (T_{i}, V_{o c}) (t_{i}^{a} - t_{i - 1}^{a})), \end{matrix}$

where:

V_oc is the Normalized open-circuit voltage during storage, V/Vnom.
R₀ is the Internal resistance.
t_i is the time sample derived from the Vector of time intervals parameter.
T_i is derived from the Vector of temperatures parameter.
b is the Linear scaling for voltage, b.
c is the Constant offset for voltage, c.
d is the Temperature-dependent exponential increase, d.
a is the Time exponent, a.
q is the electron's elementary charge, in C.
k is the Boltzmann constant, in J/K.

The R1_age_multiplier variable in the Simscape Results Explorer stores the calendar aging of the battery in terms of resistance increase:

$R 1_a g e_m u l t i p l i e r = \frac{R}{R_{0}} .$

For thermal modeling options of the block, if you set the Storage condition parameter to Fixed open-circuit voltage, you must specify the additional Open-circuit voltage measurement temperature parameter to convert the storage open-circuit voltage to the temperature-independent state of charge during storage:

$S O C = \frac{O C V (1 - β (T_{O C V_{m e a s u r e m e n t}}))}{1 - β (T_{O C V_{m e a s u r e m e n t}}) O C V} .$

The open-circuit voltage according to the storage temperature is then defined by this equation:

$O C V_{T_{s t o r a g e}} = \frac{S O C}{1 - β (T_{s t o r a g e}) (1 - β (T_{s t o r a g e}) S O C)} .$

Finally, this equation defines the terminal resistance increase of the battery due to calendar aging according to the storage temperature:

$R = R_{0} (1 + \sum_{i = 1}^{i = n} α_{r} (T_{s t o r a g e_{i}}, O C V_{T_{s t o r a g e_{i}}}) (t_{i}^{a} - t_{i - 1}^{a})) .$

Variables

To set the priority and initial target values for the block variables before simulation, use the Initial Targets section in the block dialog box or Property Inspector. For more information, see Set Priority and Initial Target for Block Variables.

Use nominal values to specify the expected magnitude of a variable in a model. Using system scaling based on nominal values increases the simulation robustness. Nominal values can come from different sources. One of these sources is the Nominal Values section in the block dialog box or Property Inspector. For more information, see System Scaling by Nominal Values.

When you model battery fade, the Discharge cycles variable lets you specify the number of charge-discharge cycles completed prior to the start of simulation. If you disable battery fade modeling, this variable is not used by the block.

Plot Basic Voltage-Charge Characteristics

You can plot the basic voltage-charge characteristics of the Battery block without building a complete model. Use the plots to explore the impact of your parameter choices on device characteristics. If you parameterize the block from a datasheet, you can compare your plots to the datasheet to check that you parameterized the block correctly. If you have a complete working model but do not know which manufactured part to use, you can compare your plots to datasheets to help you decide.

To plot the basic characteristics, right-click the block and select Battery > Basic characteristics from the context menu. For more information about the Basic characteristics option, see Plot Basic Voltage-Charge Characteristics of Battery Blocks.

Assumptions and Limitations

The self-discharge resistance is assumed not to depend strongly on the number of discharge cycles.
For the thermal modeling option of the battery, you provide fade data only for the reference temperature operation. The block applies the same derived λ_AH, λ_R0, and λ_V1 multipliers to parameter values corresponding to the second temperature.
When using the thermal block modeling options, use caution when operating at temperatures outside of the temperature range bounded by the Measurement temperature and Second measurement temperature values. The block uses linear interpolation for the derived equation coefficients, and simulation results can become nonphysical outside of the specified range. The block checks that the internal series resistance, self-discharge resistance, and nominal voltage always remain positive. If there is a violation, the block issues error messages.

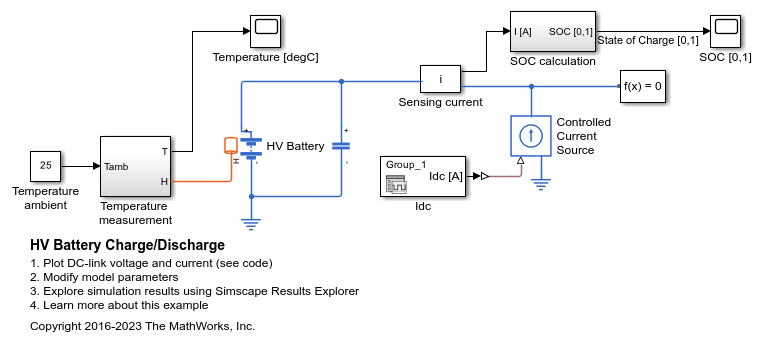
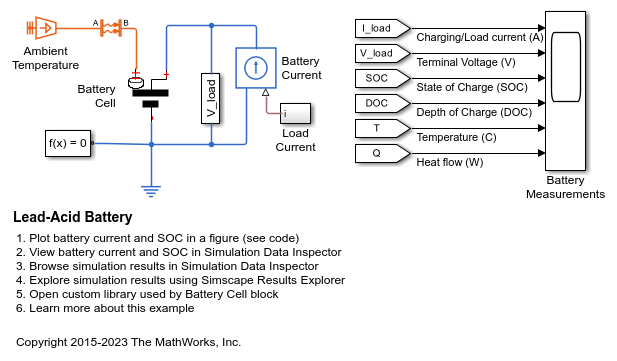
Examples

HV Battery Charge/Discharge

A high-voltage battery like those used in hybrid electric vehicles. The model uses a realistic DC-link current profile, which originates from a dynamic driving cycle. The total simulation time is 3600 seconds.

Open Model

Lead-Acid Battery

Model a lead-acid battery cell using the Simscape™ language to implement the nonlinear equations of the equivalent circuit components. In this way, as opposed to modeling entirely in Simulink®, the connection between model components and the defining physical equations is more easily understood. For the defining equations and their validation, see Jackey, R. "A Simple, Effective Lead-Acid Battery Modeling Process for Electrical System Component Selection", SAE World Congress & Exhibition, April 2007, ref. 2007-01-0778.

Ports

Output

expand all

q — Battery charge level, C
physical signal

Physical signal port that outputs the internal charge, in the units of coulomb (C). Use this output port to change load behavior as a function of charge, without the complexity of building a charge state estimator.

Dependencies

To enable this port, set Expose charge measurement port to Yes.

Conserving

expand all

+ — Positive terminal
electrical

Electrical conserving port associated with the battery positive terminal.

- — Negative terminal
electrical

Electrical conserving port associated with the battery negative terminal.

H — Battery thermal mass
thermal

Thermal conserving port that represents the battery thermal mass. When you expose this port, provide additional parameters to define battery behavior at a second temperature. For more information, see Modeling Thermal Effects.

Dependencies

To enable this port, in the Thermal Port section, set Thermal port to Model.

Parameters

expand all

Main

Nominal voltage, Vnom — Output voltage when battery is fully charged
`12` `V` (default) | positive number

No-load voltage across the battery when it is fully charged.

Current directionality — Enable direction of current
`Disabled` (default) | `Enabled`

Whether to enable current directionality. If you set this parameter to Enabled, the terminal resistance depends on the direction of the current.

Internal resistance — Battery internal resistance
`2` `Ohm` (default) | positive number

Internal connection resistance of the battery.

Dependencies

To enable this parameter, set Current directionality to Disabled.

Internal resistance during charging — Battery internal resistance during charge
`2` `Ohm` (default) | positive number

Internal connection resistance of the battery during charge phase.

Dependencies

To enable this parameter, set Current directionality to Enabled.

Internal resistance during discharging — Battery internal resistance during discharge
`2` `Ohm` (default) | positive number

Internal connection resistance of the battery during discharge phase.

Dependencies

To enable this parameter, set Current directionality to Enabled.

Battery charge capacity — Select battery model
`Infinite` (default) | `Finite`

Select one of the options for modeling the charge capacity of the battery:

Infinite — The battery voltage is independent of charge drawn from the battery.
Finite — The battery voltage decreases as charge decreases.

Cell capacity (Ah rating) — Nominal battery capacity when fully charged
`50` `hr*A` (default) | positive number

Maximum (nominal) battery charge in ampere-hours. To specify a target value for the initial battery charge at the start of simulation, use the high-priority Charge variable. For more information, see Variables.

Dependencies

To enable this parameter, set Battery charge capacity to Finite.

Voltage V1 when charge is AH1 — Output voltage at charge level AH1
`11.5` `V` (default) | positive number

Fundamental battery output voltage when the charge level is AH1, as specified by the Charge AH1 when no-load voltage is V1 parameter. This parameter must be less than Nominal voltage, Vnom.

Dependencies

To enable this parameter, set Battery charge capacity to Finite.

Charge AH1 when no-load voltage is V1 — Charge level when the no-load output voltage is V1
`25` `hr*A` (default) | positive number

Battery charge level corresponding to the no-load output voltage specified by the Voltage V1 when charge is AH1 parameter.

Dependencies

To enable this parameter, set Battery charge capacity to Finite.

Self-discharge — Select whether to model the self-discharge resistance of the battery
`Disabled` (default) | `Enabled`

Select whether to model the self-discharge resistance of the battery. The block models this effect as a resistor across the terminals of the fundamental battery model.

As temperature increases, self-discharge resistance decreases, causing self-discharge to increase. If the decrease in resistance is too fast, thermal runaway of the battery and numerical instability can occur. You can resolve this by doing any of the following:

Decrease the thermal resistance
Decrease the gradient of the self-discharge resistance with respect to temperature
Increase the self-discharge resistance

Dependencies

To enable this parameter, set Battery charge capacity to Finite.

Self-discharge resistance — Resistance that represents battery self-discharge
`2000` `Ohm` (default) | positive number

Resistance across the fundamental battery model that represents battery self-discharge.

Dependencies

To enable this parameter, set Self-discharge to Enabled.

Measurement temperature — Temperature at which the block parameters are measured
`298.15` `K` (default) | positive number

Temperature T₁, at which the block parameters in the Main section are measured. For more information, see Modeling Thermal Effects.

Dependencies

To enable this parameter, in the Thermal Port section, set Thermal port to Model.

Expose charge measurement port — Whether to expose charge measurement port
`No` (default) | `Yes`

Since R2023a

Whether to expose the charge measurement port and measure the internal charge level of the battery.

Dynamics

Charge dynamics — Battery charge dynamics model
`No dynamics` (default) | `One time-constant dynamics` | `Two time-constant dynamics` | `Three time-constant dynamics` | `Four time-constant dynamics` | `Five time-constant dynamics`

Select how to model battery charge dynamics. This parameter determines the number of parallel RC sections in the equivalent circuit:

No dynamics — The equivalent circuit contains no parallel RC sections. There is no delay between terminal voltage and internal charging voltage of the battery.
One time-constant dynamics — The equivalent circuit contains one parallel RC section. Specify the time constant using the First time constant parameter.
Two time-constant dynamics — The equivalent circuit contains two parallel RC sections. Specify the time constants using the First time constant and Second time constant parameters.
Three time-constant dynamics — The equivalent circuit contains three parallel RC sections. Specify the time constants using the First time constant, Second time constant, and Third time constant parameters.
Four time-constant dynamics — The equivalent circuit contains four parallel RC sections. Specify the time constants using the First time constant, Second time constant, Third time constant, and Fourth time constant parameters.
Five time-constant dynamics — The equivalent circuit contains five parallel RC sections. Specify the time constants using the First time constant, Second time constant, Third time constant, Fourth time constant, and Fifth time constant parameters.

First polarization resistance — First RC resistance
`0.005` `Ohm` (default) | positive number

Resistance of the first parallel RC section. This parameter primarily affects the ohmic losses of the RC section.

Dependencies

To enable this parameter, set Charge dynamics to One time-constant dynamics, Two time-constant dynamics, Three time-constant dynamics, Four time-constant dynamics, or Five time-constant dynamics.

First time constant — First RC time constant
`30` `s` (default) | positive number

Time constant of the first parallel RC section. This value is equal to RC and affects the dynamics of the RC section.

Dependencies

Second polarization resistance — Second RC resistance
`0.005` `Ohm` (default) | positive number

Resistance of the second parallel RC section. This parameter primarily affects the ohmic losses of the RC section.

Dependencies

To enable this parameter, set Charge dynamics to Two time-constant dynamics, Three time-constant dynamics, Four time-constant dynamics, or Five time-constant dynamics.

Second time constant — Second RC time constant
`30` `s` (default) | positive number

Time constant of the second parallel RC section. This value is equal to RC and affects the dynamics of the RC section.

Dependencies

To enable this parameter, set Charge dynamics to Two time-constant dynamics, Three time-constant dynamics, Four time-constant dynamics, or Five time-constant dynamics.

Third polarization resistance — Third RC resistance
`0.005` `Ohm` (default) | positive number

Resistance of the third parallel RC section. This parameter primarily affects the ohmic losses of the RC section.

Dependencies

To enable this parameter, set Charge dynamics to Three time-constant dynamics, Four time-constant dynamics, or Five time-constant dynamics.

Third time constant — Third RC time constant
`30` `s` (default) | positive number

Time constant of the third parallel RC section. This value is equal to RC and affects the dynamics of the RC section.

Dependencies

To enable this parameter, set Charge dynamics to Three time-constant dynamics, Four time-constant dynamics, or Five time-constant dynamics.

Fourth polarization resistance — Fourth RC resistance
`0.005` `Ohm` (default) | positive number

Resistance of the fourth parallel RC section. This parameter primarily affects the ohmic losses of the RC section.

Dependencies

To enable this parameter, set Charge dynamics to Four time-constant dynamics or Five time-constant dynamics.

Fourth time constant — Fourth RC time constant
`30` `s` (default) | positive number

Time constant of the fourth parallel RC section. This value is equal to RC and affects the dynamics of the RC section.

Dependencies

To enable this parameter, set Charge dynamics to Four time-constant dynamics or Five time-constant dynamics.

Fifth polarization resistance — Fifth RC resistance
`0.005` `Ohm` (default) | positive number

Resistance of the fifth parallel RC section. This parameter primarily affects the ohmic losses of the RC section.

Dependencies

To enable this parameter, set Charge dynamics to Five time-constant dynamics.

Fifth time constant — Fifth RC time constant
`30` `s` (default) | positive number

Time constant of the fifth parallel RC section. This value is equal to RC and affects the dynamics of the RC section.

Dependencies

To enable this parameter, set Charge dynamics to Five time-constant dynamics.

Fade

Battery fade — Select whether to model battery performance deterioration with aging
`Disabled` (default) | `Enabled`

Select whether to include battery fade modeling:

Disabled — The battery performance is not age dependent.
Enabled — The battery performance changes depending on the number of completed charge-discharge cycles. Selecting this option exposes additional parameters in this section, which define the battery performance after a certain number of discharge cycles. The block uses these parameter values to calculate the scaling coefficients k₁, k₂, and k₃. For more information, see Modeling Battery Fade.

Dependencies

To enable this parameter, in the Main section, set Battery charge capacity to Finite. If Battery charge capacity is Infinite, the Fade section is empty.

Number of discharge cycles, N — Number of cycles that defines a second set of data points
`100` (default) | positive number

Number of charge-discharge cycles after which the other parameters in this section are measured. This second set of data points defines the scaling coefficients k₁, k₂, and k₃, used in modeling battery fade.

Dependencies

To enable this parameter, set Battery fade to Enabled.

Cell capacity after N discharge cycles — Maximum battery capacity after N discharge cycles
`45` `hr*A` (default) | positive number

Maximum battery charge, in ampere-hours, after the number of discharge cycles specified by the Number of discharge cycles, N parameter.

Dependencies

To enable this parameter, set Battery fade to Enabled.

Internal resistance after N discharge cycles — Battery internal resistance after N discharge cycles
`2.02` `Ohm` (default) | positive number

Battery internal resistance after the number of discharge cycles specified by the Number of discharge cycles, N parameter.

Dependencies

To enable this parameter, set Battery fade to Enabled and, in the Main section, set Current Directionality to Disabled.

Average internal resistance after N discharge cycles — Battery average internal resistance after N discharge cycles
`2.02` `Ohm` (default) | positive number

Average of the battery charge and discharge internal resistance after the number of discharge cycles specified by the Number of discharge cycles, N parameter.

Dependencies

To enable this parameter, set Battery fade to Enabled and, in the Main section, set Current Directionality to Enabled.

Voltage V1 at charge AH1 after N discharge cycles — Output voltage at charge level AH1 after N discharge cycles
`10.35` `V` (default) | positive number

Fundamental battery model output voltage, at charge level AH1, after the number of discharge cycles specified by the Number of discharge cycles, N parameter.

Dependencies

To enable this parameter, set Battery fade to Enabled.

Calendar Aging

To expose these parameters, in the Main tab, set Battery charge capacity to Finite.

Calendar aging — Calendar aging option
`Disabled` (default) | `Enabled`

Whether to enable calendar aging of the battery.

Storage condition — Storage condition
`Fixed open-circuit voltage` (default) | `Fixed state of charge`

Whether to specify the open-circuit voltage or the state of charge during storage.

Dependencies

To enable this parameter, set Calendar aging to Enabled.

Normalized open-circuit voltage during storage, V/Vnom — Normalized open-circuit voltage during storage
`0.9` (default) | scalar

Normalized open-circuit voltage during storage.

Dependencies

To enable this parameter, set Calendar aging to Enabled and Storage condition to Fixed open-circuit voltage.

Open-circuit measurement temperature — Open-circuit temperature
`298.15` `K` (default) | positive number

Open-circuit measurement temperature.

Dependencies

To enable this parameter, expose the block thermal port and set Calendar aging to Enabled and Storage condition to Fixed open-circuit voltage.

State of charge during storage (%) — Percentage state of charge during storage
`60` (default) | positive number

State of charge during storage, in percentage.

Dependencies

To enable this parameter, set Calendar aging to Enabled and Storage condition to Fixed state of charge.

Vector of time intervals — Time intervals
`[0]` `d` (default) | scalar

Time intervals. This parameter must be equal in size to Vector of temperatures.

Dependencies

To enable this parameter, set Calendar aging to Enabled.

Vector of temperatures — Storage temperatures
`[273]` `K` (default) | scalar

Set of storage temperatures. This parameter must be equal in size to Vector of time intervals.

Dependencies

To enable this parameter, set Calendar aging to Enabled.

Linear scaling for voltage, b — Voltage linear scaling
`2.2134e6` (default) | scalar

Linear scaling coefficient for open-circuit voltage.

Dependencies

To enable this parameter, set Calendar aging to Enabled.

Constant offset for voltage, c — Voltage constant offset
`1.632e6` (default) | scalar

Constant offset for open-circuit voltage.

Dependencies

To enable this parameter, set Calendar aging to Enabled.

Temperature-dependent exponential increase, d — Temperature-dependent exponential increase
`0.515833569` `V` (default) | scalar

Temperature-dependent exponential increase.

Dependencies

To enable this parameter, set Calendar aging to Enabled.

Time exponent, a — Time exponent
`0.75` (default) | scalar

Time exponent.

Dependencies

To enable this parameter, set Calendar aging to Enabled.

Temperature Dependence

This section appears only for blocks with exposed thermal port. To expose the thermal port, in the Thermal Port section, set Thermal port to Model. For more information, see Modeling Thermal Effects.

Nominal voltage at second measurement temperature — Output voltage when battery is fully charged
`12` `V` (default) | positive number

No-load voltage across the battery at the second measurement temperature when it is fully charged.

Internal resistance at second measurement temperature — Battery internal resistance
`2.2` `Ohm` (default) | positive number

Internal connection resistance of the battery at the second measurement temperature.

Voltage V1 at second measurement temperature — Output voltage at charge level AH1
`11.4` `V` (default) | positive number

Fundamental battery model output voltage at the second measurement temperature and at charge level AH1, as specified by the Charge AH1 when no-load voltage is V1 parameter.

Dependencies

To enable this parameter, in the Main section, set Battery charge capacity parameter to Finite.

Self-discharge resistance at second measurement temperature — Resistance that represents battery self-discharge
`2200` `Ohm` (default) | positive number

Resistance across the fundamental battery model at the second measurement temperature. This resistance represents the self-discharge.

Dependencies

To enable this parameter, in the Main section, set Self-discharge resistance parameter to Enabled.

First polarization resistance at second measurement temperature — First RC resistance at second measurement temperature
`0.005` `Ohm` (default) | positive number

Resistance of the first parallel RC section at the second measurement temperature.

Dependencies

First time constant at second measurement temperature — First RC time constant at second measurement temperature
`30` `s` (default) | positive number

Time constant of the first parallel RC section at the second measurement temperature.

Dependencies

Second polarization resistance at second measurement temperature — Second RC resistance at second measurement temperature
`0.005` `Ohm` (default) | positive number

Resistance of the second parallel RC section at the second measurement temperature.

Dependencies

To enable this parameter, set Charge dynamics to Two time-constant dynamics, Three time-constant dynamics, Four time-constant dynamics, or Five time-constant dynamics.

Second time constant at second measurement temperature — Second RC time constant at second measurement temperature
`30` `s` (default) | positive number

Time constant of the second parallel RC section at the second measurement temperature.

Dependencies

To enable this parameter, set Charge dynamics to Two time-constant dynamics, Three time-constant dynamics, Four time-constant dynamics, or Five time-constant dynamics.

Third polarization resistance at second measurement temperature — Third RC resistance at second measurement temperature
`0.005` `Ohm` (default) | positive number

Resistance of the third parallel RC section at the second measurement temperature.

Dependencies

To enable this parameter, set Charge dynamics to Three time-constant dynamics, Four time-constant dynamics, or Five time-constant dynamics.

Third time constant at second measurement temperature — Third RC time constant at second measurement temperature
`30` `s` (default) | positive number

Time constant of the third parallel RC section at the second measurement temperature.

Dependencies

To enable this parameter, set Charge dynamics to Three time-constant dynamics, Four time-constant dynamics, or Five time-constant dynamics.

Fourth polarization resistance at second measurement temperature — Fourth RC resistance at second measurement temperature
`0.005` `Ohm` (default) | positive number

Resistance of the fourth parallel RC section at the second measurement temperature.

Dependencies

To enable this parameter, set Charge dynamics to Four time-constant dynamics or Five time-constant dynamics.

Fourth time constant at second measurement temperature — Fourth RC time constant at second measurement temperature
`30` `s` (default) | positive number

Time constant of the fourth parallel RC section at the second measurement temperature.

Dependencies

To enable this parameter, set Charge dynamics to Four time-constant dynamics or Five time-constant dynamics.

Fifth polarization resistance at second measurement temperature — Fifth RC resistance at second measurement temperature
`0.005` `Ohm` (default) | positive number

Resistance of the fifth parallel RC section at the second measurement temperature.

Dependencies

To enable this parameter, set Charge dynamics to Five time-constant dynamics.

Fifth time constant at second measurement temperature — Fifth RC time constant at second measurement temperature
`30` `s` (default) | positive number

Time constant of the fifth parallel RC section at the second measurement temperature.

Dependencies

To enable this parameter, set Charge dynamics to Five time-constant dynamics.

Second measurement temperature — Temperature at which the block parameters in this section are measured
`273.15` `K` (default) | positive number

Temperature T₂, at which the block parameters in the Temperature Dependence section are measured. For more information, see Modeling Thermal Effects.

To specify the initial temperature at the start of simulation, use the high-priority Temperature variable. For more information, see Variables.

Thermal Port

Thermal port — Whether to expose thermal port
`Omit` (default) | `Model`

Since R2023a

Whether to expose the thermal port of the block and simulate the thermal effects of the battery.

Thermal mass — Thermal mass associated with the thermal port
`30000` `J/K` (default) | positive number

Thermal mass associated with the thermal port H. It represents the energy required to raise the temperature of the thermal port by one degree.

Dependencies

To enable this parameter, set Thermal port to Model.

References

[1] Ramadass, P., B. Haran, R. E. White, and B. N. Popov. “Mathematical Modeling of the Capacity Fade of Li-Ion Cells.” Journal of Power Sources 123, no. 2 (September 2003): 230–240. https://doi.org/10.1016/S0378-7753(03)00531-7.

[2] Ning, G., B. Haran, and B. N. Popov. “Capacity Fade Study of Lithium-Ion Batteries Cycled at High Discharge Rates.” Journal of Power Sources 117, no. 1-2 (May 2003): 160–169. https://doi.org/10.1016/S0378-7753(03)00029-6.

[3] Schmalstieg, J., S. Käbitz, M. Ecker, and D. U. Sauer. “A Holistic Aging Model for Li(NiMnCo)O₂ Based 18650 Lithium-Ion Batteries.” Journal of Power Sources 257 (July 2014): 325–334. https://doi.org/10.1016/j.jpowsour.2014.02.012.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced in R2008b

expand all

R2023a: The Modeling option parameter has been replaced

The Modeling option parameter of the block has been removed and replaced with the Expose charge measurement port and Thermal port parameters. To expose the internal charge output port, set the Expose charge measurement port parameter to Yes. To expose the thermal port and simulate the thermal effects, set the Thermal port parameter to Model.

As a result of this change, if you have created a custom component by using the Battery block in an earlier release, you must update the custom component accordingly.

For batteryecm.battery_thermal: 
charge_measurement_port=simscape.enum.thermaleffects.model

For batteryecm.battery_instrumented: 
charge_measurement_port=simscape.enum.battery.enable.yes

For batteryecm.battery_thermal_instrumented: 
charge_measurement_port=simscape.enum.thermaleffects.model 
charge_measurement_port=simscape.enum.battery.enable.yes

Battery

Description

Battery Model

Modeling Battery Fade

Modeling Thermal Effects

Modeling Charge Dynamics

Modeling Battery Aging

Variables

Plot Basic Voltage-Charge Characteristics

Assumptions and Limitations

Examples

HV Battery Charge/Discharge

Lead-Acid Battery

Ports

Output

q — Battery charge level, C physical signal

Dependencies

Conserving

+ — Positive terminal electrical

- — Negative terminal electrical

H — Battery thermal mass thermal

Dependencies

Parameters

Main

Nominal voltage, Vnom — Output voltage when battery is fully charged 12 V (default) | positive number

Current directionality — Enable direction of current Disabled (default) | Enabled

Internal resistance — Battery internal resistance 2 Ohm (default) | positive number

Dependencies

Internal resistance during charging — Battery internal resistance during charge 2 Ohm (default) | positive number

Dependencies

Internal resistance during discharging — Battery internal resistance during discharge 2 Ohm (default) | positive number

Dependencies

Battery charge capacity — Select battery model Infinite (default) | Finite

Cell capacity (Ah rating) — Nominal battery capacity when fully charged 50 hr*A (default) | positive number

Dependencies

Voltage V1 when charge is AH1 — Output voltage at charge level AH1 11.5 V (default) | positive number

Dependencies

Charge AH1 when no-load voltage is V1 — Charge level when the no-load output voltage is V1 25 hr*A (default) | positive number

Dependencies

Self-discharge — Select whether to model the self-discharge resistance of the battery Disabled (default) | Enabled

Dependencies

Self-discharge resistance — Resistance that represents battery self-discharge 2000 Ohm (default) | positive number

Dependencies

Measurement temperature — Temperature at which the block parameters are measured 298.15 K (default) | positive number

Dependencies

Expose charge measurement port — Whether to expose charge measurement port No (default) | Yes

Dynamics

Charge dynamics — Battery charge dynamics model No dynamics (default) | One time-constant dynamics | Two time-constant dynamics | Three time-constant dynamics | Four time-constant dynamics | Five time-constant dynamics

First polarization resistance — First RC resistance 0.005 Ohm (default) | positive number

Dependencies

First time constant — First RC time constant 30 s (default) | positive number

Dependencies

Second polarization resistance — Second RC resistance 0.005 Ohm (default) | positive number

Dependencies

Second time constant — Second RC time constant 30 s (default) | positive number

Dependencies

Third polarization resistance — Third RC resistance 0.005 Ohm (default) | positive number

Dependencies

Third time constant — Third RC time constant 30 s (default) | positive number

Dependencies

Fourth polarization resistance — Fourth RC resistance 0.005 Ohm (default) | positive number

Dependencies

Fourth time constant — Fourth RC time constant 30 s (default) | positive number

Dependencies

Fifth polarization resistance — Fifth RC resistance 0.005 Ohm (default) | positive number

Dependencies

Fifth time constant — Fifth RC time constant 30 s (default) | positive number

Dependencies

Fade

Battery fade — Select whether to model battery performance deterioration with aging Disabled (default) | Enabled

Dependencies

Number of discharge cycles, N — Number of cycles that defines a second set of data points 100 (default) | positive number

Dependencies

Cell capacity after N discharge cycles — Maximum battery capacity after N discharge cycles 45 hr*A (default) | positive number

Dependencies

Internal resistance after N discharge cycles — Battery internal resistance after N discharge cycles 2.02 Ohm (default) | positive number

Dependencies

Average internal resistance after N discharge cycles — Battery average internal resistance after N discharge cycles 2.02 Ohm (default) | positive number

Dependencies

Voltage V1 at charge AH1 after N discharge cycles — Output voltage at charge level AH1 after N discharge cycles 10.35 V (default) | positive number

q — Battery charge level, C
physical signal

+ — Positive terminal
electrical

- — Negative terminal
electrical

H — Battery thermal mass
thermal

Nominal voltage, Vnom — Output voltage when battery is fully charged
`12` `V` (default) | positive number

Current directionality — Enable direction of current
`Disabled` (default) | `Enabled`

Internal resistance — Battery internal resistance
`2` `Ohm` (default) | positive number

Internal resistance during charging — Battery internal resistance during charge
`2` `Ohm` (default) | positive number

Internal resistance during discharging — Battery internal resistance during discharge
`2` `Ohm` (default) | positive number

Battery charge capacity — Select battery model
`Infinite` (default) | `Finite`

Cell capacity (Ah rating) — Nominal battery capacity when fully charged
`50` `hr*A` (default) | positive number

Voltage V1 when charge is AH1 — Output voltage at charge level AH1
`11.5` `V` (default) | positive number

Charge AH1 when no-load voltage is V1 — Charge level when the no-load output voltage is V1
`25` `hr*A` (default) | positive number

Self-discharge — Select whether to model the self-discharge resistance of the battery
`Disabled` (default) | `Enabled`

Self-discharge resistance — Resistance that represents battery self-discharge
`2000` `Ohm` (default) | positive number

Measurement temperature — Temperature at which the block parameters are measured
`298.15` `K` (default) | positive number

Expose charge measurement port — Whether to expose charge measurement port
`No` (default) | `Yes`

Charge dynamics — Battery charge dynamics model
`No dynamics` (default) | `One time-constant dynamics` | `Two time-constant dynamics` | `Three time-constant dynamics` | `Four time-constant dynamics` | `Five time-constant dynamics`

First polarization resistance — First RC resistance
`0.005` `Ohm` (default) | positive number

First time constant — First RC time constant
`30` `s` (default) | positive number

Second polarization resistance — Second RC resistance
`0.005` `Ohm` (default) | positive number

Second time constant — Second RC time constant
`30` `s` (default) | positive number

Third polarization resistance — Third RC resistance
`0.005` `Ohm` (default) | positive number

Third time constant — Third RC time constant
`30` `s` (default) | positive number

Fourth polarization resistance — Fourth RC resistance
`0.005` `Ohm` (default) | positive number

Fourth time constant — Fourth RC time constant
`30` `s` (default) | positive number

Fifth polarization resistance — Fifth RC resistance
`0.005` `Ohm` (default) | positive number

Fifth time constant — Fifth RC time constant
`30` `s` (default) | positive number

Battery fade — Select whether to model battery performance deterioration with aging
`Disabled` (default) | `Enabled`

Number of discharge cycles, N — Number of cycles that defines a second set of data points
`100` (default) | positive number

Cell capacity after N discharge cycles — Maximum battery capacity after N discharge cycles
`45` `hr*A` (default) | positive number

Internal resistance after N discharge cycles — Battery internal resistance after N discharge cycles
`2.02` `Ohm` (default) | positive number

Average internal resistance after N discharge cycles — Battery average internal resistance after N discharge cycles
`2.02` `Ohm` (default) | positive number

Voltage V1 at charge AH1 after N discharge cycles — Output voltage at charge level AH1 after N discharge cycles
`10.35` `V` (default) | positive number

Calendar aging — Calendar aging option
`Disabled` (default) | `Enabled`

Storage condition — Storage condition
`Fixed open-circuit voltage` (default) | `Fixed state of charge`

Normalized open-circuit voltage during storage, V/Vnom — Normalized open-circuit voltage during storage
`0.9` (default) | scalar

Open-circuit measurement temperature — Open-circuit temperature
`298.15` `K` (default) | positive number

State of charge during storage (%) — Percentage state of charge during storage
`60` (default) | positive number

Vector of time intervals — Time intervals
`[0]` `d` (default) | scalar

Vector of temperatures — Storage temperatures
`[273]` `K` (default) | scalar

Linear scaling for voltage, b — Voltage linear scaling
`2.2134e6` (default) | scalar

Constant offset for voltage, c — Voltage constant offset
`1.632e6` (default) | scalar

Temperature-dependent exponential increase, d — Temperature-dependent exponential increase
`0.515833569` `V` (default) | scalar

Time exponent, a — Time exponent
`0.75` (default) | scalar

Nominal voltage at second measurement temperature — Output voltage when battery is fully charged
`12` `V` (default) | positive number

Internal resistance at second measurement temperature — Battery internal resistance
`2.2` `Ohm` (default) | positive number

Voltage V1 at second measurement temperature — Output voltage at charge level AH1
`11.4` `V` (default) | positive number

Self-discharge resistance at second measurement temperature — Resistance that represents battery self-discharge
`2200` `Ohm` (default) | positive number

First polarization resistance at second measurement temperature — First RC resistance at second measurement temperature
`0.005` `Ohm` (default) | positive number

First time constant at second measurement temperature — First RC time constant at second measurement temperature
`30` `s` (default) | positive number

Second polarization resistance at second measurement temperature — Second RC resistance at second measurement temperature
`0.005` `Ohm` (default) | positive number

Second time constant at second measurement temperature — Second RC time constant at second measurement temperature
`30` `s` (default) | positive number

Third polarization resistance at second measurement temperature — Third RC resistance at second measurement temperature
`0.005` `Ohm` (default) | positive number

Third time constant at second measurement temperature — Third RC time constant at second measurement temperature
`30` `s` (default) | positive number

Fourth polarization resistance at second measurement temperature — Fourth RC resistance at second measurement temperature
`0.005` `Ohm` (default) | positive number

Fourth time constant at second measurement temperature — Fourth RC time constant at second measurement temperature
`30` `s` (default) | positive number

Fifth polarization resistance at second measurement temperature — Fifth RC resistance at second measurement temperature
`0.005` `Ohm` (default) | positive number

Fifth time constant at second measurement temperature — Fifth RC time constant at second measurement temperature
`30` `s` (default) | positive number

Second measurement temperature — Temperature at which the block parameters in this section are measured
`273.15` `K` (default) | positive number

Thermal port — Whether to expose thermal port
`Omit` (default) | `Model`

Thermal mass — Thermal mass associated with the thermal port
`30000` `J/K` (default) | positive number

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.