Model Fault-Tolerant Fuel Control System

Analysis and Physics

Physical and empirical relationships form the basis for the throttle and intake manifold dynamics of this model. The model computes air-fuel ratio by dividing the air mass flow rate pumped from the intake manifold by the fuel mass flow rate injected at the valves. The stoichiometric mixture ratio provides a good compromise between power, fuel economy, and emissions. The target air-fuel ratio for this system is 14.6. Typically, a sensor determines the amount of residual oxygen present in the exhaust gas (EGO). This measurement gives a good indication of the mixture ratio and provides a feedback measurement for closed-loop control. If the sensor indicates a high oxygen level, the control law increases the fuel rate. When the sensor detects a fuel-rich mixture, the controller decreases the fuel rate.

Modeling

Open the model. To run the simulation, in the Simulink Toolstrip, on the Simulation tab, click Run.

The model uses a callback function to load the data required for the simulation into the model workspace from the sldemo_fuelsys_data file. Loading initial conditions into the model workspace keeps simulation data isolated from data in any other open models and helps avoid cluttering MATLAB® workspace cluttering. To view the contents of the model workspace, in the Simulink Editor, on the Modeling tab, in the Design section, expand the gallery and click Model Explorer. In the Model Explorer window, in the Model Hierarchy list on the left, expand sldemo_fuelsys and select Model Workspace. For more information about how to use callbacks to load simulation data, see Automatically Initialize Variables and Load Data (Simulink).

The model logs relevant data to MATLAB workspace in a data structure called sldemo_fuelsys_output and streams the data to the Simulation Data Inspector. Logged signals are marked with a blue badge. To learn more about data logging, see Save Signal Data Using Signal Logging (Simulink).

Note that units are visible on the model and subsystem icons and signal lines. Units are specified on the ports and on the bus object.

The Dashboard subsystem allows you to interact with the model during simulation. Fault Injection switches from the Normal to Fail position to simulate sensor failures. Toggle the Engine Speed selector switch to change the engine speed. You can visualize the fuel and air-fuel ratio signals using gauges and scopes. The blocks in the Dashboard subsystem are from the Dashboard library. To learn about dashboard blocks, see Control Simulations with Interactive Displays (Simulink).

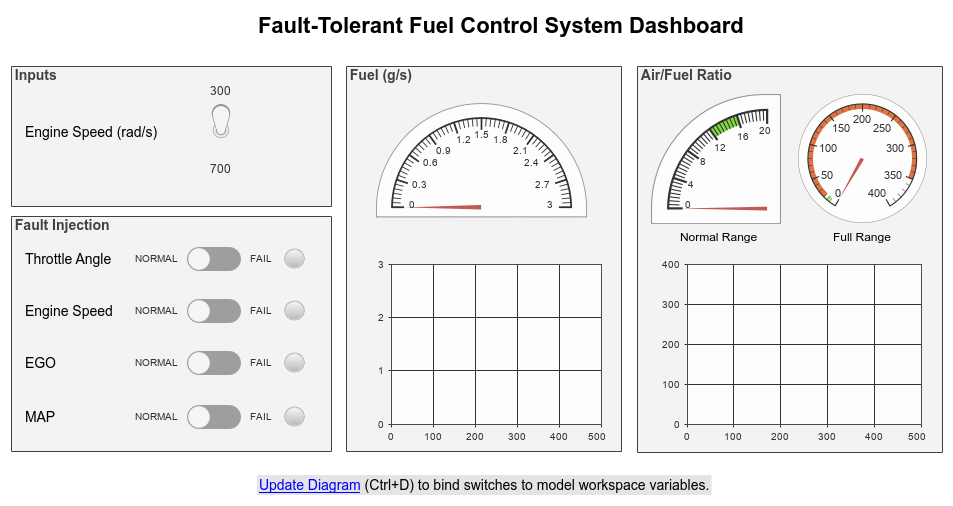
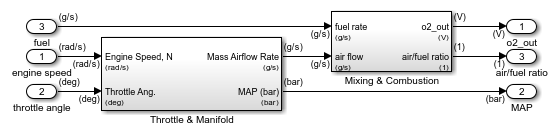
The fuel_rate_control subsystem uses signals from the system sensors to determine the fuel rate which gives a stoichiometric mixture. The fuel rate combines with the actual air flow in the engine gas dynamics model to determine the resulting mixture ratio as sensed at the exhaust.

You can simulate the failure of any of the throttle angle, speed, EGO, or manifold absolute pressure (MAP) sensors by switching off the corresponding slider switch in the dashboard subsystem. To access the switches, double-click the subsystem block named Dashboard. To flip a switch, click where you want the handle of the switch to move. If you stop the simulation, select the Slider Switch block, and then click where you want the handle to move. Each slider switch connects to the value parameter of a Constant block. When you switch off the slider switch, you change the value of the Constant block.

Similarly, you can induce the failure condition of a high engine speed by toggling the engine speed switch on the dashboard subsystem. A Repeating Table block provides the throttle angle input and periodically repeats the sequence of data specified in the mask.

The fuel_rate_control subsystem uses the sensor input and feedback signals to adjust the fuel rate to give a stoichiometric ratio. The model uses three subsystems to implement this strategy: one for control logic, one for airflow calculation, and one for fuel calculation. Under normal operation, the model estimates the airflow rate and multiplies the estimate by the reciprocal of the desired ratio to give the fuel rate. Feedback from the oxygen sensor provides a closed-loop adjustment of the rate estimation to maintain the ideal mixture ratio.

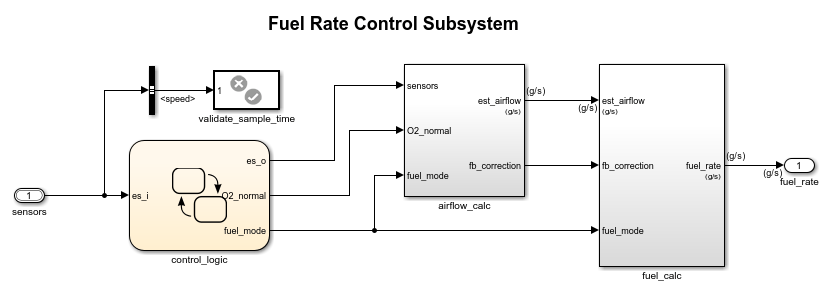
Control Logic

A single Stateflow chart, consisting of a set of six parallel states, implements the control logic in its entirety. The four parallel states shown at the top of the chart correspond to the four individual sensors. The remaining two parallel states consider the status of the four sensors simultaneously and determine the overall system operating mode. The model synchronously calls the entire Stateflow diagram at a regular sample time interval of 0.01 sec. This interval allows timely testing of the conditions for transitions to the correct mode.

If you enable animation in the Stateflow debugger, the state transitions are highlighted in the Stateflow diagram as the various states are activated. The sequence of activation is indicated by changing colors. This closely coupled synergy between Stateflow and Simulink fosters the modeling and development of complete control systems.

To open the control_logic Stateflow chart, double-click the chart in the fuel_rate_control subsystem.

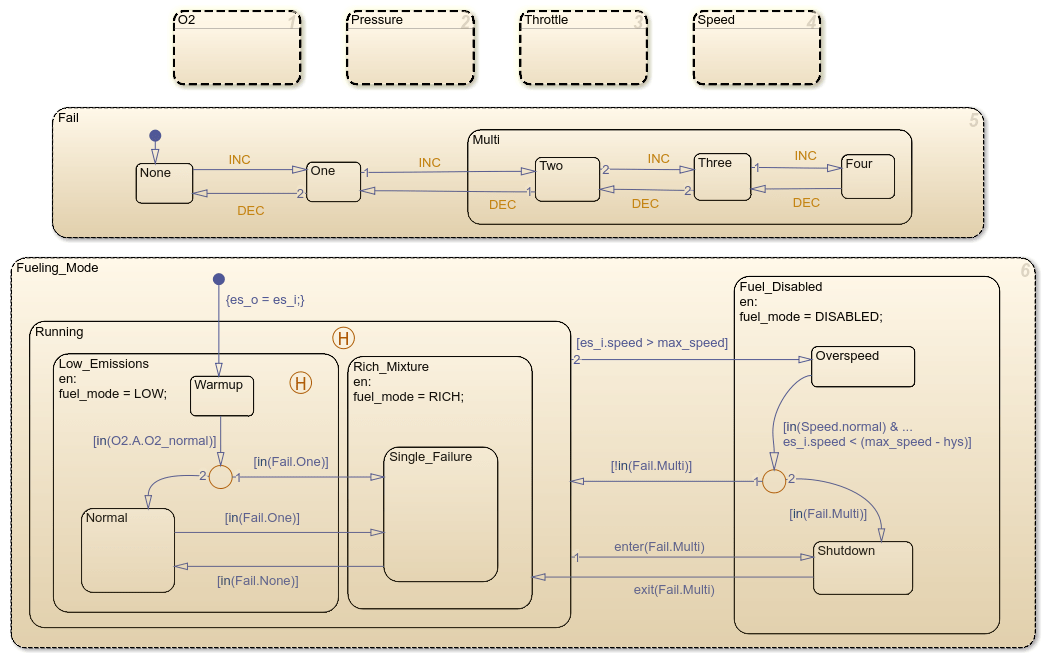
When execution begins, all states start in normal mode with the exception of the oxygen sensor (EGO). The initial O2_warmup state persists until the warmup period is complete. The system detects throttle and pressure sensor failures when their measured values fall outside their nominal ranges. A manifold vacuum in the absence of a speed signal indicates a speed sensor failure. The oxygen sensor also has a nominal range for failure conditions. However, because zero is both the minimum signal level and the bottom of the range, the system can detect failure only when the sensor exceeds the upper limit.

Regardless of which sensor fails, the model always generates the directed event broadcast Fail.INC. In this way, the triggering of the universal sensor failure logic is independent of the sensor. The model also uses a corresponding sensor recovery event, Fail.DEC. The Fail state keeps track of the number of failed sensors. The counter increments on each Fail.INC event and decrements on each Fail.DEC event. The model uses a superstate, Multi, to group all cases where more than one sensor has failed.

The bottom parallel state represents the fueling mode of the engine. If a single sensor fails, operation continues, but the air-fuel mixture is richer to allow smoother running at the cost of higher emissions. If more than one sensor fails, the air-fuel ratio cannot be controlled reliably, so the engine shuts down as a safety measure.

During the oxygen sensor warm-up, the model maintains the mixture at normal levels. You can change the design by moving the warm-up state to within the Rich_Mixture superstate. If a sensor failure occurs during the warm-up period, the Single_Failure state is entered after the warm-up time elapses. Otherwise, the Normal state is activated at this time.

A protective overspeed feature is added to the model by creating a new state in the Fuel_Disabled superstate. Through the use of history junctions, the model ensures that the chart returns to the appropriate state when the model exits the overspeed state. With this approach, you can add additional shutdown states to the Fuel_Disabled superstate if you want to specify additional safety requirements.

Sensor Correction

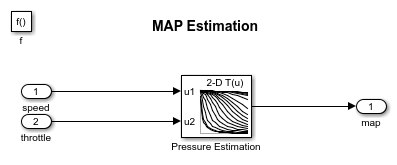
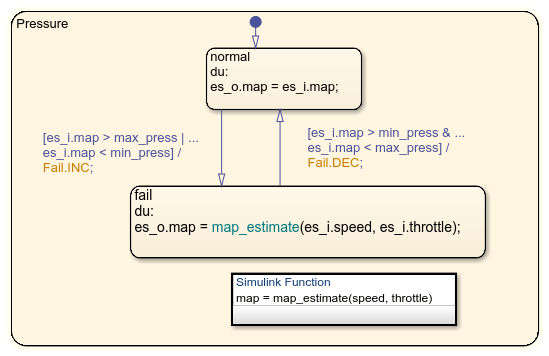
When a sensor fails, the model computes an estimate of the sensor. For example,open the pressure sensor calculation. Under normal sensor operation, the model uses the value of the pressure sensor. Otherwise, the model estimates the value.

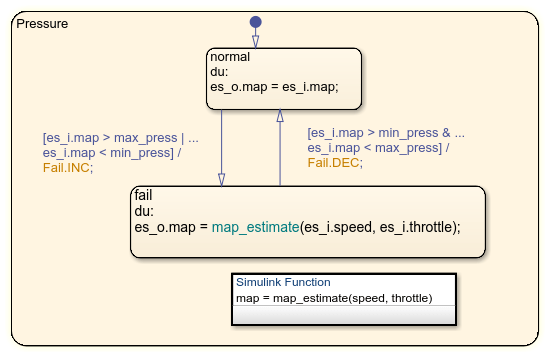
The model computes an estimate of manifold pressure as a function of the engine speed and throttle position. To compute the value, the model uses a Simulink function in Stateflow.

Airflow Calculation

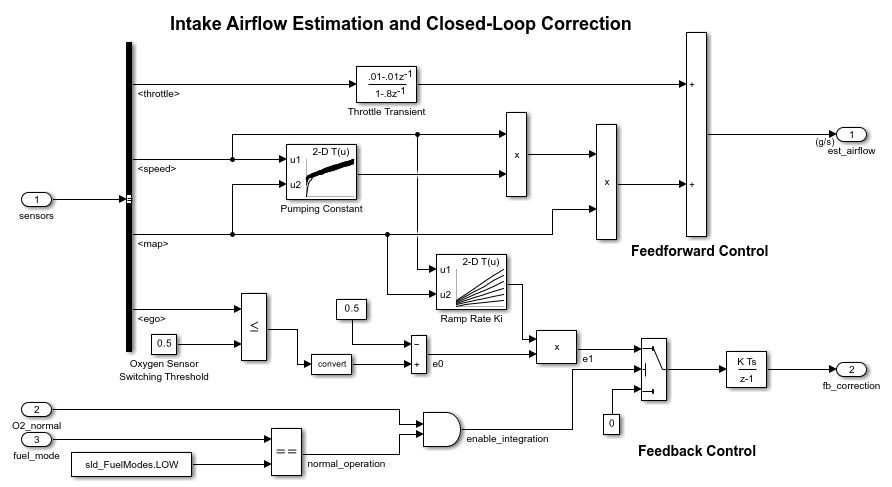
The airflow_calc subsystem is the location for the central control laws. This block is inside the fuel_rate_control subsystem. The subsystem estimates the intake air flow to determine the fuel rate that gives the appropriate air-fuel ratio. Closed-loop control adjusts the estimation according to the residual oxygen feedback in order to maintain the mixture ratio precisely. Even when a sensor failure mandates open-loop operation, the most recent closed-loop adjustment is retained to best meet the control objectives.

Equation 1

You can formulate the engine intake air flow as the product of the engine speed, the manifold pressure, and a time-varying scale factor.

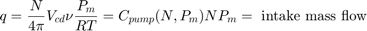
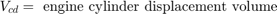
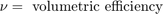
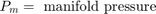
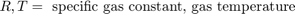
Cpump is computed by a lookup table and multiplied by the speed and pressure to form the initial flow estimate. During transients, the throttle rate, with the derivative approximated by a high-pass filter, corrects the air flow for filling dynamics. The control algorithm provides additional correction according to Equation 2.

Equation 2

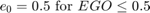
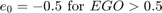
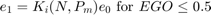
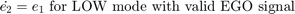
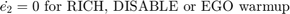
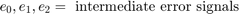
The nonlinear oxygen sensor is modeled using the MATLAB Function block named EGO Sensor. To view the block, from the top level of the model, enter the Engine Gas Dynamics subsystem. Then, enter the Mixing & Combustion subsystem.

The EGO sensor is modeled as a hyperbolic tangent function and provides a meaningful signal when in the vicinity of 0.5 volt. The raw error in the feedback loop is thus detected with a switching threshold, as indicated in Equation 2. If the air-fuel ratio is low (the mixture is lean), the original air estimate is too small and needs to be increased. Conversely, when the oxygen sensor output is high, the air estimate is too large and needs to be decreased. Integral control is utilized so that the correction term achieves a level that brings about zero steady-state error in the mixture ratio.

The normal closed-loop operation mode, low, adjusts the integrator dynamically to minimize the error. The integration is performed in discrete time, with updates every 10 milliseconds. When operating in an open loop however, in the rich or O2 failure modes, the feedback error is ignored and the integrator is held. These actions gives the best correction based on the most recent valid feedback.

Fuel Calculation

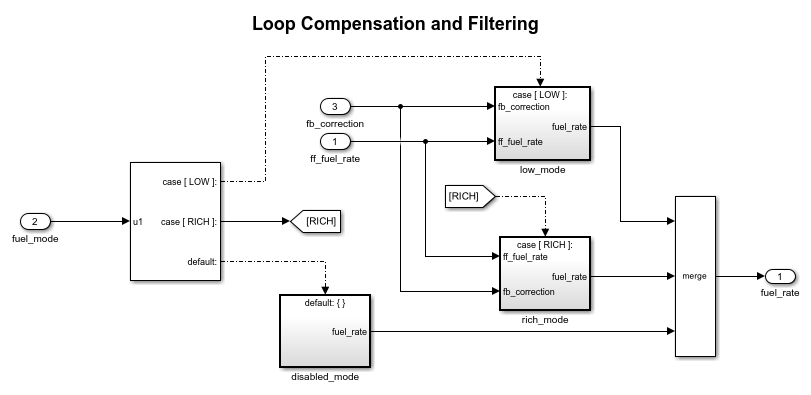
The fuel_rate_control subsystem contains a subsystem named fuel_calc. The fuel_calc subsystem sets the injector signal to match the given airflow calculation and fault status. The first input to the subsystem is the computed airflow estimation. This value is multiplied with the target fuel-air ratio to get the commanded fuel rate. Normally, the target is stoichiometric, which is to say that the target equals the optimal air to fuel ratio of 14.6. When a sensor fault occurs, the Stateflow control logic sets the mode input to a value of 2 or 3 (rich or disabled) so that the mixture is either slightly rich of stoichiometric or is shut down completely.

The fuel_calc subsystem employs adjustable compensation to achieve different purposes in different modes. In normal operation, phase lead compensation of the feedback correction signal adds to the closed-loop stability margin. In rich mode and during EGO sensor failure (open-loop operation), however, the composite fuel signal is low-pass filtered to attenuate noise introduced in the estimation process. The end result is a signal representing the fuel flow rate that would be translated to injector pulse times in an actual system.

Results and Conclusions

The simulation runs with a throttle input that ramps from 10 to 20 degrees over a period of two seconds, then goes back to 10 degrees over the next two seconds. This cycle repeats continuously while the engine is held at a constant speed so that you can experiment with different fault conditions and failure modes.

Click a sensor fault switch in the dashboard subsystem to simulate the failure of the associated sensor. Repeat this operation to slide the switch back for normal operation.

Now, run the simulation with different sensors turned off. Plot the fuel flow rate and air-fuel ratio for these scenarios:

Examine the fuel flow rate plots. In the baseline case, the fuel rate is regulated tightly, exhibiting a small ripple due to the switching nature of the input circuitry of the EGO sensor. In the other four cases, the system operates in an open loop. The control strategy effectively in maintains the correct fuel profile in the single-failure mode. In each of the fault conditions, the fuel rate is essentially 125% of the baseline flow, fulfilling the design objective of the fuel being 80% rich.

In each case, note the nonlinear relationship between fuel flow and the triangular throttle command.

Examine the air-fuel ratio plots. The baseline plot shows the effects of closed-loop operation. The mixture ratio is regulated very tightly to the stoichiometric objective of 14.6. The rich mixture ratio is shown in the bottom four plots. Although the ratios are not tightly regulated, as in the closed-loop case, they approximate the desired air-fuel ratio: 0.8*14.6=11.7.

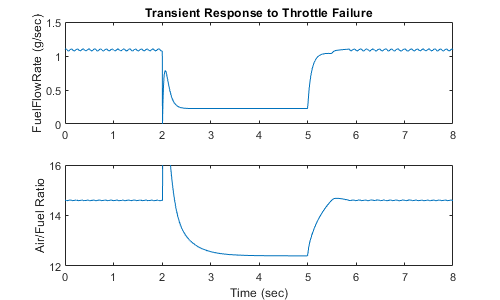
Examine the transient behavior of the system. With a constant throttle angle of 12 degrees and the system in steady-state, a throttle failure is introduced at t = 2 and corrected at t = 5. At the onset of the failure, the fuel rate increases immediately. You can see the effects at the exhaust as the rich ratio propagates through the system. The steady-state condition then quickly recovers when closed-loop operation is restored.