Operations for Fixed-Point Data in Stateflow

Stateflow^® charts in Simulink^® models have an action language property that defines the syntax that you use to compute with fixed-point data:

MATLAB^® as the action language.
C as the action language.

For more information, see Differences Between MATLAB and C as Action Language Syntax.

Binary Operations

This table summarizes the interpretation of all binary operations on fixed-point operands according to their order of precedence (0 = highest, 9 = lowest). Binary operations are left associative so that, in any expression, operators with the same precedence are evaluated from left to right.

Unary Operations and Actions

This table summarizes the interpretation of all unary operations and actions on fixed-point operands. Unary operations:

Have higher precedence than binary operators.
Are right associative so that, in any expression, they are evaluated from right to left.

Operation	MATLAB as the Action Language	C as the Action Language
`~a`	Not supported. Use the expression `a == cast(0,"like",a)`. See Logical Operations for Fixed-Point Data.	Logical NOT. Enable this operation by clearing the Enable C-bit operations chart property. See Logical Operations for Fixed-Point Data and Enable C-bit operations.
`!a`	Not supported. Use the expression `a == cast(0,"like",a)`. See Logical Operations for Fixed-Point Data.	Logical NOT. See Logical Operations for Fixed-Point Data.
`-a`	Negative. See Unary Minus.	Negative. See Unary Minus.
`a++`	Not supported. Use the expression `a = a+1`.	Increment. Equivalent to `a = a+1`.
`a--`	Not supported. Use the expression `a = a-1`.	Decrement. Equivalent to `a = a-1`.

Assignment Operations

This table summarizes the interpretation of assignment operations on fixed-point operands.

Operation	MATLAB as the Action Language	C as the Action Language
`a = b`	Simple assignment.	Simple assignment.
`a := b`	Not supported. To override fixed-point promotion rules, use explicit type cast operations. See Type Cast Operations.	Special assignment that overrides fixed-point promotion rules. See Override Fixed-Point Promotion in C Charts.
`a += b`	Not supported. Use the expression `a = a+b`.	Equivalent to `a = a+b`.
`a -= b`	Not supported. Use the expression `a = a-b`.	Equivalent to `a = a-b`.
`a *= b`	Not supported. Use the expression `a = a*b`.	Equivalent to `a = a*b`.
`a /= b`	Not supported. Use the expression `a = a/b`.	Equivalent to `a = a/b`.

Override Fixed-Point Promotion in C Charts

In charts that use C as the action language, a simple assignment of the form a = b calculates an intermediate value for b according to the fixed-point promotion rules. Then this intermediate value is cast to the type of a by using an online conversion. See Promotion Rules for Fixed-Point Operations and Conversion Operations. Simple assignments are most efficient when both types have equal bias and slopes that either are equal or are both powers of two.

In contrast, a special assignment of the form a := b overrides this behavior by initially using the type of a as the result type for the value of b.

Constants in b are converted to the type of a by using offline conversions.
The expression b can contain at most one arithmetic operator (+, -, *, or /). The result is determined by using an online conversion.
If b contains anything other than an arithmetic operation or a constant, then the special assignment operation behaves like the simple assignment operation (=).

Use the special assignment operation := when you want to:

Avoid an overflow in an arithmetic operation. For example, see Avoid Overflow in Fixed-Point Addition.
Retain precision in a multiplication or division operation. For example, see Improve Precision in Fixed-Point Division.

Note

Using the special assignment operation := can result in generated code that is less efficient than the code you generate by using the normal fixed-point promotion rules.

Avoid Overflow in Fixed-Point Addition

You can use the special assignment operation := to avoid overflow when performing an arithmetic operation on two fixed-point numbers. For example, consider a chart that computes the sum a+b where a = 2¹²-1 = 4095 and b = 1.

Suppose that:

Both inputs are signed 16-bit fixed-point numbers with three fraction bits (type fixdt(1,16,3)).
The output c is a signed 32-bit fixed-point number with three fraction bits (type fixdt(1,32,3)).
The integer word size for production targets is 16 bits.

Because the target integer size is 16 bits, the simple assignment c = a+b adds the inputs in 16 bits before casting the sum to 32 bits. The intermediate result is 4096, which, as a type fixdt(1,16,3) value, results in an overflow.

In contrast, the special assignment c := a+b casts the inputs to 32 bits before computing the sum. The result of 4096 is safely computed as a type fixdt(1,32,3) value without an overflow.

Improve Precision in Fixed-Point Division

You can use the special assignment operation := to obtain a more precise result when multiplying or dividing two fixed-point numbers. For example, consider a chart that computes the ratio a/b where a = 2 and b = 3.

Suppose that:

The input a is a fixed-point number with four fraction bits (type fixdt(1,16,4)).
The input b is a fixed-point number with three fraction bits (type fixdt(1,16,3)).
The output c is a signed 16-bit fixed-point number with six fraction bits (type fixdt(1,16,6)).

The inputs correspond to these slopes and quantized integers:

S_a = 2^–4, Q_a = 32

S_b = 2^–3, Q_b = 24.

The simple assignment c = a/b first calculates an intermediate value for a/b according to the fixed-point promotion rules. The quantized integer is rounded to the floor:

S_int = S_a/S_b = 2^-4/2^-3 = 2^-1

Q_int = Q_a/Q_b = 32/24 ≈ 1.

The intermediate result is then cast as a signed 16-digit fixed-point number with six fraction bits:

S_c = 2^-6 = 1/64

Q_c = S_intQ_int/S_c = 2^-1/2^-6 = 2⁵ = 32.

Therefore, the approximate real-world value for c is V_c ≈ S_cQ_c = 32/64 = 0.5. This result is not a good approximation of the actual value of 2/3.

In contrast, the special assignment c := a/b calculates a/b directly as a signed 16-digit fixed-point number with six fraction bits. Again, the quantized integer is rounded to the floor:

S_c = 2^-6 = 1/64

Q_c = (S_aQ_a)/(S_cS_bQ_b) = 128/3 ≈ 42.

Therefore, the approximate real-world value for c is V_c ≈ S_cQ_c = 42/64 = 0.6563. This result is a better approximation to the actual value of 2/3.

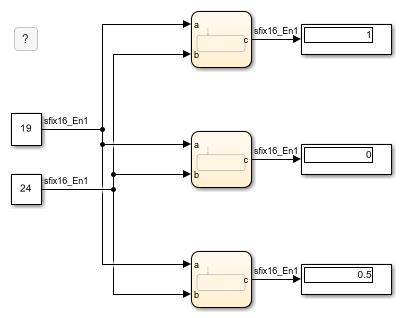
Compare Results of Fixed-Point Arithmetic

This example uses:

Open Model

This example shows the difference between various implementations of fixed-point arithmetic in Stateflow charts. The model contains three charts that calculate the ratio a/b where a = 19 and b = 24. Both inputs are signed 16-digit fixed-point numbers with one fraction bit (type fixdt(1,16,1)). They correspond to these slopes and quantized integers:

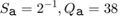
$S_\texttt{a} = 2^{-1}, Q_\texttt{a} = 38$

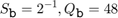
$S_\texttt{b} = 2^{-1}, Q_\texttt{b} = 48$

The model calculates the value of a/b as a floating-point number of type fixdt(1,16,1) in three different ways:

A type casting operation in a chart that uses MATLAB as the action language.
A simple assignment operation in a chart that uses C as the action language.
A special assignment operation in a chart that uses C as the action language.

Type Casting in Chart That Uses MATLAB as the Action Language

The chart at the top of the model computes an intermediate value for a/b. The quantized integer for the intermediate value is rounded to the nearest integer:

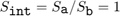
$S_\texttt{int} = S_\texttt{a}/S_\texttt{b} = 1$

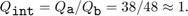
$Q_\texttt{int} = Q_\texttt{a}/Q_\texttt{b} = 38/48 \approx 1 .$

The intermediate value is then cast as a signed 16-digit fixed-point number c with one fraction bit:

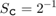
$S_\texttt{c} = 2^{-1}$

$Q_\texttt{c} = S_\texttt{int} \cdot Q_\texttt{int} /S_\texttt{c} = 2
.$

The output value from this chart is

$\tilde{V}_\texttt{c} = S_\texttt{c} \cdot Q_\texttt{c} = 1 .$

Simple Assignment in Chart That Uses C as the Action Language

The middle chart also computes an intermediate value for a/b. In this case, the quantized integer for the intermediate value is rounded to the floor:

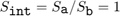
$S_\texttt{int} = S_\texttt{a}/S_\texttt{b} = 1$

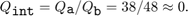
$Q_\texttt{int} = Q_\texttt{a}/Q_\texttt{b} = 38/48 \approx 0 .$

The intermediate value is then cast as a signed 16-digit fixed-point number c with one fraction bit:

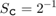
$S_\texttt{c} = 2^{-1}$

$Q_\texttt{c} = S_\texttt{int} \cdot Q_\texttt{int} /S_\texttt{c} = 0
.$

The output value from this chart is

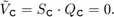
$\tilde{V}_\texttt{c} = S_\texttt{c} \cdot Q_\texttt{c} = 0 .$

Special Assignment in Chart That Uses C as the Action Language

The chart at the bottom of the model uses a special assignment of the form c := a/b. The value of the division is calculated directly as a signed 16-digit fixed-point number with one fraction bit. The quantized integer is rounded to the floor:

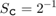
$S_\texttt{c} = 2^{-1}$

$Q_\texttt{c} = (S_\texttt{a} \cdot Q_\texttt{a}) / (S_\texttt{c} \cdot
S_\texttt{b} \cdot Q_\texttt{b}) = 19/12 \approx 1 .$

Therefore, the output value from this chart is

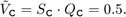
$\tilde{V}_\texttt{c} = S_\texttt{c} \cdot Q_\texttt{c} = 0.5 .$

The three results exhibit loss of precision compared to the floating-point answer of 19/24 = 0.7917. To minimize the loss of precision to an acceptable level in your application, adjust the encoding scheme in your fixed-point data.

Operation	Precedence	MATLAB as the Action Language	C as the Action Language
`a ^ b`	0	Power. Not supported for fixed-point operands defined by using either a slope that is not an integer power of two or a nonzero bias. Exponent operand must be a constant whose value is a non-negative integer.	Power. Enable this operation by clearing the Enable C-bit operations chart property. See Enable C-bit operations.
`a * b`	1	Multiplication. For fixed-point operands defined by using either a slope that is not an integer power of two or a nonzero bias, specify a chart `fimath` object with `ProductMode` set to `SpecifyPrecision`. See Multiplication.	Multiplication. Not supported for fixed-point operands defined by using a nonzero bias. See Multiplication.
`a / b`	1	Division. Not supported for fixed-point operands defined by using either a slope that is not an integer power of two or a nonzero bias. See Division.	Division. Not supported for fixed-point operands defined by using a nonzero bias. See Division.
`a + b`	2	Addition. For fixed-point operands defined by using either a slope that is not an integer power of two or a nonzero bias, specify a chart `fimath` object with `SumMode` set to `SpecifyPrecision`. See Addition and Subtraction.	Addition. See Addition and Subtraction.
`a - b`	2	Subtraction. For fixed-point operands defined by using either a slope that is not an integer power of two or a nonzero bias, specify a chart `fimath` object with `SumMode` set to `SpecifyPrecision`. See Addition and Subtraction.	Subtraction. See Addition and Subtraction.
`a > b`	3	Comparison, greater than. See Relational Operations for Fixed-Point Data.	Comparison, greater than. Not supported for fixed-point operands with mismatched biases. See Relational Operations for Fixed-Point Data.
`a < b`	3	Comparison, less than. See Relational Operations for Fixed-Point Data.	Comparison, less than. Not supported for fixed-point operands with mismatched biases. See Relational Operations for Fixed-Point Data.
`a >= b`	3	Comparison, greater than or equal to. See Relational Operations for Fixed-Point Data.	Comparison, greater than or equal to. Not supported for fixed-point operands with mismatched biases. See Relational Operations for Fixed-Point Data.
`a <= b`	3	Comparison, less than or equal to. See Relational Operations for Fixed-Point Data.	Comparison, less than or equal to. Not supported for fixed-point operands with mismatched biases. See Relational Operations for Fixed-Point Data.
`a == b`	4	Comparison, equal to. See Relational Operations for Fixed-Point Data.	Comparison, equal to. Not supported for fixed-point operands with mismatched biases. See Relational Operations for Fixed-Point Data.
`a ~= b`	4	Comparison, not equal to. See Relational Operations for Fixed-Point Data.	Comparison, not equal to. Not supported for fixed-point operands with mismatched biases. See Relational Operations for Fixed-Point Data.
`a != b`	4	Not supported. Use the operation `a ~= b`. See Relational Operations for Fixed-Point Data.	Comparison, not equal to. Not supported for fixed-point operands with mismatched biases. See Relational Operations for Fixed-Point Data.
`a <> b`	4	Not supported. Use the operation `a ~= b`. See Relational Operations for Fixed-Point Data.	Comparison, not equal to. Not supported for fixed-point operands with mismatched biases. See Relational Operations for Fixed-Point Data.
`a && b`	8	Logical AND. See Logical Operations for Fixed-Point Data.	Logical AND. See Logical Operations for Fixed-Point Data.
`a \|\| b`	9	Logical OR. See Logical Operations for Fixed-Point Data.	Logical OR. See Logical Operations for Fixed-Point Data.