logp
Log unconditional probability density of naive Bayes classification model for incremental learning
Since R2021a
Syntax
Description
lp = logp(Mdl,X)lp of the observations in the predictor data X using the naive Bayes classification model for incremental learning Mdl. You can use lp to identify outliers in the training data.
Examples
Train a naive Bayes classification model by using fitcnb, convert it to an incremental learner, and then use the incremental model to detect outliers in streaming data.
Load and Preprocess Data
Load the human activity data set. Randomly shuffle the data.
load humanactivity rng(1); % For reproducibility n = numel(actid); idx = randsample(n,n); X = feat(idx,:); Y = actid(idx);
For details on the data set, enter Description at the command line.
Train Naive Bayes Classification Model
Fit a naive Bayes classification model to a random sample of about 25% of the data.
idxtt = randsample([true false false false],n,true); TTMdl = fitcnb(X(idxtt,:),Y(idxtt))
TTMdl =
ClassificationNaiveBayes
ResponseName: 'Y'
CategoricalPredictors: []
ClassNames: [1 2 3 4 5]
ScoreTransform: 'none'
NumObservations: 6167
DistributionNames: {1×60 cell}
DistributionParameters: {5×60 cell}
Properties, Methods
TTMdl is a ClassificationNaiveBayes model object representing a traditionally trained model.
Convert Trained Model
Convert the traditionally trained model to a naive Bayes classification model for incremental learning.
IncrementalMdl = incrementalLearner(TTMdl)
IncrementalMdl =
incrementalClassificationNaiveBayes
IsWarm: 1
Metrics: [1×2 table]
ClassNames: [1 2 3 4 5]
ScoreTransform: 'none'
DistributionNames: {1×60 cell}
DistributionParameters: {5×60 cell}
Properties, Methods
IncrementalMdl is an incrementalClassificationNaiveBayes object. IncrementalMdl represents a naive Bayes classification model for incremental learning; the parameter values are the same as the parameters in TTMdl.
Detect Outliers
Determine an unconditional density threshold for outliers by using the traditionally trained model and training data. Outliers are observations in the streaming data that yield densities lower than the threshold.
ttlp = logp(TTMdl,X(idxtt,:)); [~,lower] = isoutlier(ttlp)
lower = -336.0424
Detect these outliers in the rest of the data. Simulate a data stream by processing 1 observation at a time. At each iteration, call logp to compute the log unconditional probability density of the observation and store each value.
% Preallocation idxil = ~idxtt; nil = sum(idxil); numObsPerChunk = 1; nchunk = floor(nil/numObsPerChunk); lp = zeros(nchunk,1); iso = false(nchunk,1); Xil = X(idxil,:); Yil = Y(idxil); % Incremental processing for j = 1:nchunk ibegin = min(nil,numObsPerChunk*(j-1) + 1); iend = min(nil,numObsPerChunk*j); idx = ibegin:iend; lp(j) = logp(IncrementalMdl,Xil(idx,:)); iso(j) = lp(j) < lower; end
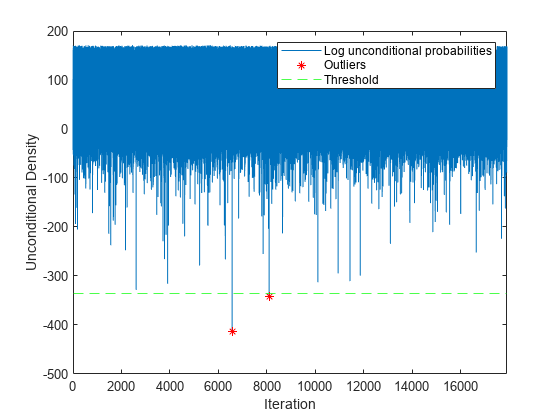
Plot the log unconditional probability densities of the streaming data. Identify the outliers.
figure; h1 = plot(lp); hold on x = 1:nchunk; h2 = plot(x(iso),lp(iso),'r*'); h3 = yline(lower,'g--'); xlim([0 nchunk]); ylabel('Unconditional Density') xlabel('Iteration') legend([h1 h2 h3],["Log unconditional probabilities" "Outliers" "Threshold"]) hold off
Input Arguments
Naive Bayes classification model for incremental learning, specified as an incrementalClassificationNaiveBayes model object. You can create Mdl directly or by converting a supported, traditionally trained machine learning model using the incrementalLearner function. For more details, see the corresponding reference page.
You must configure Mdl to compute the log conditional probability densities on a batch of observations.
If
Mdlis a converted, traditionally trained model, you can compute the log conditional probabilities without any modifications.Otherwise,
Mdl.DistributionParametersmust be a cell matrix withMdl.NumPredictors> 0 columns and at least one row, where each row corresponds to each class name inMdl.ClassNames.
Batch of predictor data with which to compute the log conditional probability densities, specified as an n-by-Mdl.NumPredictors floating-point matrix.
For each j = 1 through n, if
X( contains at least one
j,:)NaN, lp( is
j)NaN.
Data Types: single | double
Output Arguments
Log unconditional probability densities, returned as an n-by-1 floating-point vector. lp( is the log unconditional probability density of the predictors evaluated at j)X(.j,:)
Data Types: single | double
More About
The unconditional probability density of the predictors is the density's distribution marginalized over the classes.
In other words, the unconditional probability density is
where π(Y = k) is the class prior probability. The conditional distribution of the data given the class (P(X1,..,XP|y = k)) and the class prior probability distributions are training options (that is, you specify them when training the classifier).
The prior probability of a class is the assumed relative frequency with which observations from that class occur in a population.
Version History
Introduced in R2021a
See Also
Objects
Functions
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
选择网站
选择网站以获取翻译的可用内容,以及查看当地活动和优惠。根据您的位置,我们建议您选择:。
您也可以从以下列表中选择网站:
如何获得最佳网站性能
选择中国网站(中文或英文)以获得最佳网站性能。其他 MathWorks 国家/地区网站并未针对您所在位置的访问进行优化。
美洲
- América Latina (Español)
- Canada (English)
- United States (English)
欧洲
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)