Main Content

reset

Reset incremental drift-aware learner

Since R2022b

collapse all in page

    Syntax

    Mdl = reset(Mdl)

    Description

    Mdl = reset(Mdl) returns the incremental drift-aware model Mdl after resetting the learned parameters of Mdl.BaseLearner and Mdl.DriftDetector. If any hyperparameters of Mdl.BaseLearner are estimated during incremental training, the reset function resets these hyperparameters as well. reset always preserves the Mdl.BaseLearner.Numpredictors property.

    For incremental classification models, reset always preserves the Mdl.BaseLearner.ClassNames property and resets Mdl.BaseLearner.Prior if prior class probabilities are "empirical".

    The fit function internally calls reset during incremental drift-aware learning. reset is suitable for using in custom workflows.

    example

    Examples

    collapse all

    Open Live Script

    Create the random concept data and the concept drift generator using the helper functions HelperRegrGenerator and HelperConceptDriftGenerator, respectively.

    concept1 = HelperRegrGenerator(NumFeatures=100,NonZeroFeatures=[1,20,40,50,55], ...
    FeatureCoefficients=[4,5,10,-2,-6],NoiseStd=1.1,TableOutput=false);
concept2 = HelperRegrGenerator(NumFeatures=100,NonZeroFeatures=[10,20,45,56,80], ...
    FeatureCoefficients=[4,5,10,-2,-6],NoiseStd=1.1,TableOutput=false);
driftGenerator = HelperConceptDriftGenerator(concept1,concept2,15000,1000);

    HelperRegrGenerator generates streaming data using features and feature coefficients for regression specified in the call to the function. At each step, the function samples the predictors from a normal distribution. Then, the function computes the response using the feature coefficients and predictor values and adding a random noise from a normal distribution with mean zero and specified noise standard deviation. The software returns the data in matrices for using in incremental learners.

    HelperConceptDriftGenerator establishes the concept drift. The object uses a sigmoid function 1./(1+exp(-4*(numobservations-position)./width)) to decide the probability of choosing the first stream when generating data [3]. In this case, the position argument is 15000 and the width argument is 1000. As the number of observations exceeds the position value minus half of the width, the probability of sampling from the first stream when generating data decreases. The sigmoid function allows a smooth transition from one stream to the other. Larger width values indicate a larger transition period where both streams are approximately equally likely to be selected.

    Initiate an incremental drift-aware model for regression as follows:

    1. Create an incremental linear model for regression. Specify the linear regression model type and solver type.

    2. Initiate an incremental concept drift detector that uses the Hoeffding's Bounds Drift Detection Method with moving average (HDDMA).

    3. Using the incremental linear model and the concept drift detector, instantiate an incremental drift-aware model. Specify the training period as 6000 observations.

    baseMdl = incrementalRegressionLinear(Learner="leastsquares",Solver="sgd",EstimationPeriod=1000,Standardize=false);
dd = incrementalConceptDriftDetector("hddma",Alternative="greater",InputType="continuous",WarmupPeriod=1000);
idal = incrementalDriftAwareLearner(baseMdl,DriftDetector=dd,TrainingPeriod=6000);

    Preallocate the number of variables in each chunk and number of iterations for creating a stream of data. 

    numObsPerChunk = 10;
numIterations = 1000;

    Preallocate the variable for storing the regression error.

    ce = array2table(zeros(numIterations,2),VariableNames=["Cumulative" "Window"]);

    Simulate a data stream with incoming chunks of 10 observations each and perform incremental drift-aware learning. At each iteration:

    1. Simulate predictor data and labels, and update the drift generator using the helper function hgenerate.

    2. Call updateMetricsAndFit to update the performance metrics and fit the incremental drift-aware model to the incoming data.

    3. Track the regression error for visualization purposes.

    rng(12); % For reproducibility

for j = 1:numIterations
 
 % Generate data
 [driftGenerator,X,Y] = hgenerate(driftGenerator,numObsPerChunk); 

 % Update performance metrics and fit the model
 idal = updateMetricsAndFit(idal,X,Y); 

 % Record regression error
  ce{j,:} = idal.Metrics{"MeanSquaredError",:};
 
end

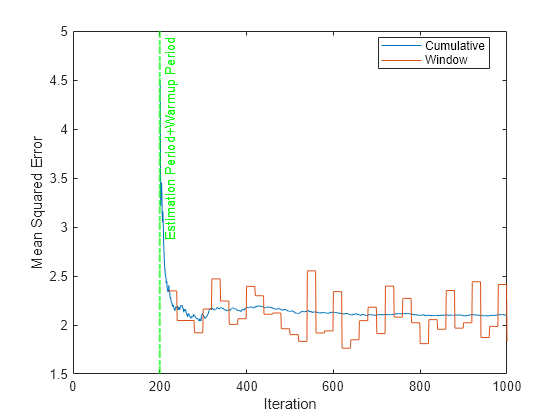
    Plot the cumulative and per window regression error. Mark the warmup plus estimation period.

    h = plot(ce.Variables);
xlim([0 numIterations])
ylabel("Mean Squared Error")
xlabel("Iteration")
xline((idal.MetricsWarmupPeriod+idal.BaseLearner.EstimationPeriod)/numObsPerChunk,"g-.","Estimation Period+Warmup Period",LineWidth=1.5)
legend(h,ce.Properties.VariableNames)
legend(h,Location="best")

    Figure contains an axes object. The axes object with xlabel Iteration, ylabel Mean Squared Error contains 3 objects of type line, constantline. These objects represent Cumulative, Window.

    Display the incremental drift-aware learner and the current metrics values. 

    idal
    idal = 
  incrementalDriftAwareLearner

           IsWarm: 1
          Metrics: [1x2 table]
      BaseLearner: [1x1 incrementalRegressionLinear]
    DriftDetector: [1x1 HoeffdingDriftDetectionMethod]
       IsTraining: 0



    idal.Metrics
    ans=1×2 table
                        Cumulative    Window
                        __________    ______

    MeanSquaredError      2.0976      1.826

    Display the base learner, and the drift detector.

    idal.BaseLearner
    ans = 
  incrementalRegressionLinear

               IsWarm: 1
              Metrics: [1x2 table]
    ResponseTransform: 'none'
                 Beta: [100x1 double]
                 Bias: -0.0793
              Learner: 'leastsquares'



    idal.BaseLearner.Beta
    ans = 100×1

    4.0221
    0.0492
    0.0046
    0.0529
   -0.0818
   -0.1161
    0.0307
   -0.0669
   -0.0103
    0.0159
      ⋮

    Display the drift detector.

    idal.DriftDetector
    ans = 
  HoeffdingDriftDetectionMethod

        PreviousDriftStatus: 'Stable'
                DriftStatus: 'Stable'
                     IsWarm: 1
    NumTrainingObservations: 7900
                Alternative: 'greater'
                  InputType: 'continuous'
                 TestMethod: 'average'

    Reset the incremental drift-aware learner. Display the model and the metrics property.

    idal = reset(idal)
    idal = 
  incrementalDriftAwareLearner

           IsWarm: 0
          Metrics: [1x2 table]
      BaseLearner: [1x1 incrementalRegressionLinear]
    DriftDetector: [1x1 HoeffdingDriftDetectionMethod]
       IsTraining: 1



    idal.Metrics
    ans=1×2 table
                        Cumulative    Window
                        __________    ______

    MeanSquaredError       NaN         NaN

    The metrics are reset to NaN values. The software will wait until idal.BaseLearner.EstimationPeriod+idal.BaseLearner.MetricsWarmUpPeriod observations have passed before computing the metrics again.

    Resetting the model resets the base learner and the underlying drift detector as well.

    Display the base learner.

    idal.BaseLearner
    ans = 
  incrementalRegressionLinear

               IsWarm: 0
              Metrics: [1x2 table]
    ResponseTransform: 'none'
                 Beta: [100x1 double]
                 Bias: 0
              Learner: 'leastsquares'

    The Bias parameter is also reset to 0.

    Display the Beta property of the base learner.

    idal.BaseLearner.Beta
    ans = 100×1

     0
     0
     0
     0
     0
     0
     0
     0
     0
     0
      ⋮

    Coefficient values are all set to 0.

    Display the drift detector.

    idal.DriftDetector
    ans = 
  HoeffdingDriftDetectionMethod

        PreviousDriftStatus: 'Stable'
                DriftStatus: 'Stable'
                     IsWarm: 0
    NumTrainingObservations: 0
                Alternative: 'greater'
                  InputType: 'continuous'
                 TestMethod: 'average'

    IsWarm property and the number of training observations are both set to 0.

    You can use the dot notation to explore how other properties of the drift-aware learner, the base learner, and the drift detector change after a reset.

    Input Arguments

    collapse all

    Incremental drift-aware learning model fit to streaming data, specified as an incrementalDriftAwareLearner model object. You can create Mdl using the incrementalDriftAwareLearner function. For more details, see the object reference page.

    Output Arguments

    collapse all

    Updated incremental drift-aware learning model, returned as an incremental learning model object of the same data type as the input model Mdl, incrementalDriftAwareLearner.

    References

    [1] Barros, Roberto S.M. , et al. "RDDM: Reactive drift detection method." Expert Systems with Applications. vol. 90, Dec. 2017, pp. 344-55. https://doi.org/10.1016/j.eswa.2017.08.023.

    [2] Bifet, Albert, et al. "New Ensemble Methods for Evolving Data Streams." Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM Press, 2009, p. 139. https://doi.org/10.1145/1557019.1557041.

    [3] Gama, João, et al. "Learning with drift detection". Advances in Artificial Intelligence – SBIA 2004, edited by Ana L. C. Bazzan and Sofiane Labidi, vol. 3171, Springer Berlin Heidelberg, 2004, pp. 286–95. https://doi.org/10.1007/978-3-540-28645-5_29.

    Version History

    Introduced in R2022b

    See Also

    | | |