canonvars

Load the fisheriris data set.

load fisheriris

The column vector species contains iris flowers of three different species: setosa, versicolor, and virginica. The matrix meas contains four types of measurements for the flower: the length and width of sepals and petals in centimeters.

Perform a one-way MANOVA with species as the factor and the measurements in meas as the response variables.

maov = manova(species,meas);

maov is a one-way manova object that contains the results of the one-way MANOVA.

Calculate the canonical response data for maov.

canon = canonvars(maov)

canon = 150×4

   -8.0618    0.3004    0.2780   -0.0147
   -7.1287   -0.7867    0.0678    0.8910
   -7.4898   -0.2654   -0.4915    0.2587
   -6.8132   -0.6706   -0.7707   -0.2776
   -8.1323    0.5145   -0.0240   -0.4797
   -7.7019    1.4617    0.3962   -0.4742
   -7.2126    0.3558   -1.0245   -0.3291
   -7.6053   -0.0116    0.0437   -0.2531
   -6.5606   -1.0152   -1.1049    0.1391
   -7.3431   -0.9473    0.0965   -0.1066
      ⋮

The output shows the canonical response data for the first ten observations. Each column of the output corresponds to a different canonical variable.

Create a scatter plot using the first and second canonical variables.

gscatter(canon(:,1),canon(:,2),species)
xlabel("canon1")
ylabel("canon2")

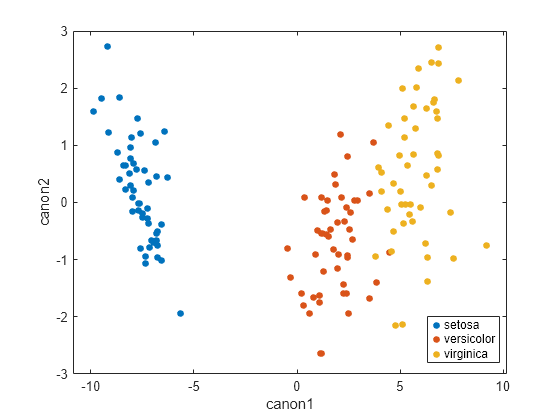
The function calculates the canonical variables by finding the lowest dimensional representation of the response variables that maximizes the correlation between the response variables and the factor values. The plot shows that the response data for the first two canonical variables is mostly separate for the different factor values. In particular, observations with the first canonical variable less than 0 correspond to the setosa group. Observations with the first canonical response variable greater than 0 and less than 5 correspond to the versicolor group. Finally, observations with the first canonical response variable greater than 5 correspond to the virginica group.

Load the carsmall data set.

load carsmall

The variable Model_Year contains data for the year a car was manufactured, and the variable Cylinders contains data for the number of engine cylinders in the car. The Acceleration and Displacement variables contain data for car acceleration and displacement.

Use the table function to create a table from the data in Model_Year and Cylinders.

tbl = table(Model_Year,Cylinders,VariableNames=["Year" "Cylinders"]);

Create a matrix of response variables from Acceleration and Displacement.

y = [Acceleration Displacement];

Perform a two-way MANOVA using the factor values in tbl and the response variables in y.

maov = manova(tbl,y);

maov is a two-way manova object that contains the results of the two-way MANOVA.

Return the canonical response data, canonical coefficients, and eigenvalues for the response data in maov, grouped by the Cylinders factor.

[canon,eigenvec,eigenval] = canonvars(maov,"Cylinders")

canon = 100×2

    2.9558   -0.5358
    4.2381   -0.4096
    3.2798   -0.8889
    2.8661   -0.5600
    2.7996   -1.2391
    6.5913   -0.4348
    7.3336   -0.6749
    6.9131   -1.0089
    7.3680   -0.2249
    5.4195   -1.4126
      ⋮

eigenvec = 2×2

    0.0045    0.4419
    0.0299    0.0081

eigenval = 2×1

    6.5170
    0.0808

The output shows the canonical response data for each canonical variable, and the vectors of canonical coefficients for each canonical variable with their corresponding eigenvalues.

You can use the coefficients in eigenvec to calculate canonical response data manually. Normalize the training data in maov.Y by using the mean function.

normres = maov.Y - mean(maov.Y)

normres = 100×2

   -3.0280   99.4000
   -3.5280  142.4000
   -4.0280  110.4000
   -3.0280   96.4000
   -4.5280   94.4000
   -5.0280  221.4000
   -6.0280  246.4000
   -6.5280  232.4000
   -5.0280  247.4000
   -6.5280  182.4000
      ⋮

Calculate the product of the matrix of normalized response data and matrix of canonical coefficients.

mcanon = normres*eigenvec

mcanon = 100×2

    2.9558   -0.5358
    4.2381   -0.4096
    3.2798   -0.8889
    2.8661   -0.5600
    2.7996   -1.2391
    6.5913   -0.4348
    7.3336   -0.6749
    6.9131   -1.0089
    7.3680   -0.2249
    5.4195   -1.4126
      ⋮

The first ten rows of mcanon are identical to the first ten rows of data in canon.

Check that mcanon is identical to canon by using the max and sum functions.

max(abs(canon-mcanon))

ans = 1×2

     0     0

The zero output confirms that the two methods of calculating the canonical response data are equivalent.