mnrfit

(Not recommended) Multinomial logistic regression

mnrfit is not recommended. Use fitmnr instead. (since R2023a) For more information see Version History.

Syntax

B = mnrfit(X,Y)

B = mnrfit(X,Y,Name,Value)

[B,dev,stats]
= mnrfit(___)

Description

B = mnrfit(X,Y) returns a matrix, B, of coefficient estimates for a multinomial logistic regression of the nominal responses in Y on the predictors in X.

example

B = mnrfit(X,Y,Name,Value) returns a matrix, B, of coefficient estimates for a multinomial model fit with additional options specified by one or more Name,Value pair arguments.

For example, you can fit a nominal, an ordinal, or a hierarchical model, or change the link function.

example

[B,dev,stats] = mnrfit(___) also returns the deviance of the fit, dev, and the structure stats for any of the previous input arguments. stats contains model statistics such as degrees of freedom, standard errors for coefficient estimates, and residuals.

example

Examples

collapse all

Multinomial Regression for Nominal Responses

Open Live Script

Fit a multinomial regression for nominal outcomes and interpret the results.

Load the sample data.

load fisheriris

The column vector, species, consists of iris flowers of three different species, setosa, versicolor, virginica. The double matrix meas consists of four types of measurements on the flowers, the length and width of sepals and petals in centimeters, respectively.

Define the nominal response variable using a categorical array.

sp = categorical(species);

Fit a multinomial regression model to predict the species using the measurements.

[B,dev,stats] = mnrfit(meas,sp);
B

B = 5×2
10³ ×

    2.0184    0.0426
    0.6739    0.0025
   -0.5682    0.0067
   -0.5164   -0.0094
   -2.7609   -0.0183

This is a nominal model for the response category relative risks, with separate slopes on all four predictors, that is, each category of meas. The first row of B contains the intercept terms for the relative risk of the first two response categories, setosa and versicolor versus the reference category, virginica. The last four rows contain the slopes for the models for the first two categories. mnrfit accepts the third category as the reference category.

The relative risk of an iris flower being species 2 (versicolor) versus species 3 (virginica) is the ratio of the two probabilities (the probability of being species 2 and the probability of being species 3). The model for the relative risk is

$\ln (\frac{π_{v e r s i c o l o r}}{π_{v i r g i n i c a}}) = 42.6 + 2.5 X_{1} + 6.7 X_{2} - 9.4 X_{3} - 18.3 X_{4} .$

The coefficients express both the effects of the predictor variables on the relative risk and the log odds of being in one category versus the reference category. For example, the estimated coefficient 2.5 indicates that the relative risk of being species 2 (versicolor) versus species 3 (virginica) increases exp(2.5) times for each unit increase in $X_{1}$ , the first measurement, given all else is equal. The relative log odds of being versicolor versus virginica increases 2.5 times with a one-unit increase in $X_{1}$ , given all else is equal.

If the coefficients are converging toward infinity or negative infinity, the estimated coefficients can vary slightly depending on your operating system.

Check the statistical significance of the model coefficients.

stats.p

ans = 5×2

         0    0.0000
         0    0.0281
         0    0.0000
         0    0.0000
         0    0.0000

The small $p$ -values indicate that all measures are significant on the relative risk of being a setosa versus a virginica (species 1 compared to species 3) and being a versicolor versus a virginica (species 2 compared to species 3).

Request the standard errors of coefficient estimates.

stats.se

ans = 5×2

   12.4038    5.2719
    3.5783    1.1228
    3.1760    1.4789
    3.5403    1.2934
    7.1203    2.0967

Calculate the 95% confidence limits for the coefficients.

LL = stats.beta - 1.96.*stats.se;
UL = stats.beta + 1.96.*stats.se;

Display the confidence intervals for the coefficients of the model for the relative risk of being a setosa versus a virginica (the first column of coefficients in B).

[LL(:,1) UL(:,1)]

ans = 5×2
10³ ×

    1.9941    2.0427
    0.6668    0.6809
   -0.5744   -0.5620
   -0.5234   -0.5095
   -2.7749   -2.7470

Find the confidence intervals for the coefficients of the model for the relative risk of being a versicolor versus a virginica (the second column of coefficients in B).

[LL(:,2) UL(:,2)]

ans = 5×2

   32.3049   52.9707
    0.2645    4.6660
    3.7823    9.5795
  -11.9644   -6.8944
  -22.3957  -14.1766

Multinomial Regression for Ordinal Responses

Open Live Script

Fit a multinomial regression model for categorical responses with natural ordering among categories.

Load the sample data and define the predictor variables.

load carbig
X = [Acceleration Displacement Horsepower Weight];

The predictor variables are the acceleration, engine displacement, horsepower, and weight of the cars. The response variable is miles per gallon (mpg).

Create an ordinal response variable categorizing MPG into four levels from 9 to 48 mpg by labeling the response values in the range 9-19 as 1, 20-29 as 2, 30-39 as 3, and 40-48 as 4.

miles = discretize(MPG,[9,19,29,39,48]);

Fit an ordinal response model for the response variable miles.

[B,dev,stats] = mnrfit(X,miles,'model','ordinal');
B

The first three elements of B are the intercept terms for the models, and the last four elements of B are the coefficients of the covariates, assumed common across all categories. This model corresponds to parallel regression, which is also called the proportional odds model, where there is a different intercept but common slopes among categories. You can specify this using the 'interactions','off' name-value pair argument, which is the default for ordinal models.

[B(1:3)'; repmat(B(4:end),1,3)]

ans = 5×3

  -16.6895  -11.7208   -8.0606
    0.1048    0.1048    0.1048
    0.0103    0.0103    0.0103
    0.0645    0.0645    0.0645
    0.0017    0.0017    0.0017

The link function in the model is logit ('link','logit'), which is the default for an ordinal model. The coefficients express the relative risk or log odds of the mpg of a car being less than or equal to one value versus greater than that value.

The proportional odds model in this example is

$\begin{array}{l} \ln (\frac{P (m p g \leq 19)}{P (m p g > 19)}) = - 16.6895 + 0.1048 X_{A} + 0.0103 X_{D} + 0.0645 X_{H} + 0.0017 X_{W} \\ \ln (\frac{P (m p g \leq 29)}{P (m p g > 29)}) = - 11.7208 + 0.1048 X_{A} + 0.0103 X_{D} + 0.0645 X_{H} + 0.0017 X_{W} \\ \ln (\frac{P (m p g \leq 39)}{P (m p g > 39)}) = - 8.0606 + 0.1048 X_{A} + 0.0103 X_{D} + 0.0645 X_{H} + 0.0017 X_{W} \end{array}$

For example, the coefficient estimate of 0.1048 indicates that a unit change in acceleration would impact the odds of the mpg of a car being less than or equal to 19 versus more than 19, or being less than or equal to 29 versus greater than 29, or being less than or equal to 39 versus greater than 39, by a factor of exp(0.01048) given all else is equal.

Assess the significance of the coefficients.

stats.p

The $p$ -values of 0.035, 0.0000, and 0.0118 for engine displacement, horsepower, and weight of a car, respectively, indicate that these factors are significant on the odds of mpg of a car being less than or equal to a certain value versus being greater than that value.

Hierarchical Multinomial Regression Model

Open Live Script

Fit a hierarchical multinomial regression model.

Load the sample data.

load('smoking.mat');

The data set smoking contains five variables: sex, age, weight, and systolic and diastolic blood pressure. Sex is a binary variable where 1 indicates female patients, and 0 indicates male patients.

Define the response variable.

Y = categorical(smoking.Smoker);

The data in Smoker has four categories:

0: Nonsmoker, 0 cigarettes a day
1: Smoker, 1–5 cigarettes a day
2: Smoker, 6–10 cigarettes a day
3: Smoker, 11 or more cigarettes a day

Define the predictor variables.

X = [smoking.Sex smoking.Age smoking.Weight...
    smoking.SystolicBP smoking.DiastolicBP];

Fit a hierarchical multinomial model.

[B,dev,stats] = mnrfit(X,Y,'model','hierarchical');
B

B = 6×3

   43.8148    5.9571   44.0712
    1.8709   -0.0230    0.0662
    0.0188    0.0625    0.1335
    0.0046   -0.0072   -0.0130
   -0.2170    0.0416   -0.0324
   -0.2273   -0.1449   -0.4824

The first column of B includes the intercept and the coefficient estimates for the model of the relative risk of being a nonsmoker versus a smoker. The second column includes the parameter estimates for modeling the log odds of smoking 1–5 cigarettes a day versus more than five cigarettes a day given that a person is a smoker. Finally, the third column includes the parameter estimates for modeling the log odds of a person smoking 6–10 cigarettes a day versus more than 10 cigarettes a day given he/she smokes more than 5 cigarettes a day.

The coefficients differ across categories. You can specify this using the 'interactions','on' name-value pair argument, which is the default for hierarchical models. So, the model in this example is

$\ln (\frac{P (y = 0)}{P (y > 0)}) = 43.8148 + 1.8709 X_{S} + 0.0188 X_{A} + 0.0046 X_{W} - 0.2170 X_{S B P} - 0.2273 X_{D B P}$

$\ln (\frac{P (1 \leq y \leq 5)}{P (y > 5)}) = 5.9571 - 0.0230 X_{S} + 0.0625 X_{A} - 0.0072 X_{W} + 0.0416 X_{S B P} - 0.1449 X_{D B P}$

$\ln (\frac{P (6 \leq y \leq 10)}{P (y > 10)}) = 44.0712 + 0.0662 X_{S} + 0.1335 X_{A} - 0.0130 X_{W} - 0.0324 X_{S B P} - 0.4824 X_{D B P}$

For example, the coefficient estimate of 1.8709 indicates that the likelihood of being a smoker versus a nonsmoker increases by exp(1.8709) = 6.49 times as the gender changes from female to male given everything else held constant.

Assess the statistical significance of the terms.

stats.p

ans = 6×3

    0.0000    0.5363    0.2149
    0.3549    0.9912    0.9835
    0.6850    0.2676    0.2313
    0.9032    0.8523    0.8514
    0.0009    0.5187    0.8165
    0.0004    0.0483    0.0545

Sex, age, or weight don’t appear significant on any level. The $p$ -values of 0.0009 and 0.0004 indicate that both types of blood pressure are significant on the relative risk of a person being a smoker versus a nonsmoker. The $p$ -value of 0.0483 shows that only diastolic blood pressure is significant on the odds of a person smoking 0–5 cigarettes a day versus more than 5 cigarettes a day. Similarly, the $p$ -value of 0.0545 indicates that diastolic blood pressure is significant on the odds of a person smoking 6–10 cigarettes a day versus more than 10 cigarettes a day.

Check if any nonsignificant factors are correlated to each other. Draw a scatterplot of age versus weight grouped by sex.

figure()
gscatter(smoking.Age,smoking.Weight,smoking.Sex)
legend('Male','Female')
xlabel('Age')
ylabel('Weight')

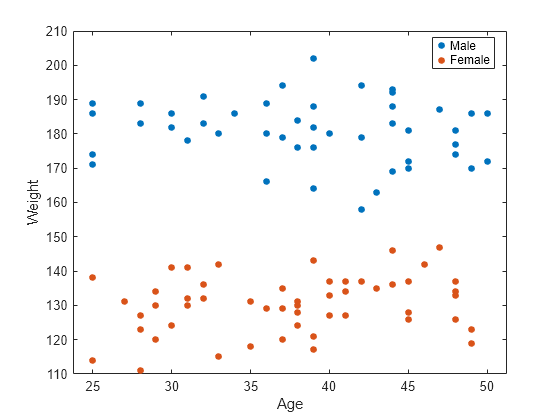
Figure contains an axes object. The axes object with xlabel Age, ylabel Weight contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent Male, Female.

The range of weight of an individual seems to differ according to gender. Age does not seem to have any obvious correlation with sex or weight. Age is insignificant and weight seems to be correlated with sex, so you can eliminate both and reconstruct the model.

Eliminate age and weight from the model and fit a hierarchical model with sex, systolic blood pressure, and diastolic blood pressure as the predictor variables.

X = double([smoking.Sex smoking.SystolicBP...
smoking.DiastolicBP]);
[B,dev,stats] = mnrfit(X,Y,'model','hierarchical');
B

B = 4×3

   44.8456    5.3230   25.0248
    1.6045    0.2330    0.4982
   -0.2161    0.0497    0.0179
   -0.2222   -0.1358   -0.3092

Here, a coefficient estimate of 1.6045 indicates that the likelihood of being a nonsmoker versus a smoker increases by exp(1.6045) = 4.97 times as sex changes from male to female. A unit increase in the systolic blood pressure indicates an exp(–.2161) = 0.8056 decrease in the likelihood of being a nonsmoker versus a smoker. Similarly, a unit increase in the diastolic blood pressure indicates an exp(–.2222) = 0.8007 decrease in the relative rate of being a nonsmoker versus being a smoker.

Assess the statistical significance of the terms.

stats.p

ans = 4×3

    0.0000    0.4715    0.2325
    0.0210    0.7488    0.6362
    0.0010    0.4107    0.8899
    0.0003    0.0483    0.0718

The $p$ -values of 0.0210, 0.0010, and 0.0003 indicate that the terms sex and both types of blood pressure are significant on the relative risk of a person being a nonsmoker versus a smoker, given the other terms in the model. Based on the $p$ -value of 0.0483, diastolic blood pressure appears significant on the relative risk of a person smoking 1–5 cigarettes versus more than 5 cigarettes a day, given that this person is a smoker. Because none of the $p$ -values on the third column are less than 0.05, you can say that none of the variables are statistically significant on the relative risk of a person smoking from 6–10 cigarettes versus more than 10 cigarettes, given that this person smokes more than 5 cigarettes a day.

Input Arguments

collapse all

`X` — Observations on predictor variables
n-by-p matrix

Observations on predictor variables, specified as an n-by-p matrix. X contains n observations for p predictors.

Note

mnrfit automatically includes a constant term (intercept) in all models. Do not include a column of 1s in X.

Data Types: single | double

`Y` — Response category labels
n-by-k matrix | n-by-1 numeric vector | n-by-1 logical vector | n-by-1 string vector | n-by-1 categorical array | n-by-1 cell array of character vectors

Response category labels, specified as an n-by-k matrix, or an n-by-1 numeric vector, logical vector, string vector, categorical array, or cell array of character vectors.

If Y is an n-by-k matrix, n is the number of observations in the data set, and k is the number of response categories. Y(i,j) is the number of outcomes of the multinomial category j for the predictor combinations given by X(i,:). In this case, the function determines the number of observations at each predictor combination.
If Y is an n-by-1 numeric vector, the vector indicates the value of the response for each observation. In this case, all sample sizes are 1. mnrfit treats the response categories as having integer values from 1 to the maximum value in Y. If Y does not include all integer values ranging from 1 to the maximum value in Y, mnrfit treats the response categories for the excluded values as having no observations.
If Y is an n-by-1 logical vector, string vector, categorical array, or cell array of character vectors, the vector or array indicates the value of the response for each observation. In this case, all sample sizes are 1.

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: 'Model','ordinal','Link','probit' specifies an ordinal model with a probit link function.

`Model` — Type of model to fit
`'nominal'` (default) | `'ordinal'` | `'hierarchical'`

Type of model to fit, specified as the comma-separated pair consisting of 'Model' and one of the following.

`'nominal'`	Default. There is no ordering among the response categories. Multinomial regression is sometimes called softmax regression when `Model` is `'nominal'`.
`'ordinal'`	There is a natural ordering among the response categories.
`'hierarchical'`	The choice of response category is sequential/nested.

Example: 'Model','ordinal'

`Interactions` — Indicator for interaction between multinomial categories and coefficients
`'on'` | `'off'`

Indicator for an interaction between the multinomial categories and coefficients, specified as the comma-separated pair consisting of 'Interactions' and one of the following.

`'on'`	Default for nominal and hierarchical models. Fit a model with different coefficients across categories.
`'off'`	Default for ordinal models. Fit a model with a common set of coefficients for the predictor variables, across all multinomial categories. This is often described as parallel regression or the proportional odds model.

In all cases, the model has different intercepts across categories. The choice of 'Interactions' determines the dimensions of the output array B.

Example: 'Interactions','off'

`IterationLimit` — Maximum number of iterations
100 (default) | positive integer

Maximum number of iteratively reweighted least squares (IRLS) iterations used to fit the model, specified as a positive integer. The default value for IterationLimit is 100.

For more information about the IRLS algorithm, see Iteratively Reweighted Least Squares.

Example: IterationLimit=400

Data Types: single | double

`Link` — Link function
`'logit'` (default) | `'probit'` | `'comploglog'` | `'loglog'`

Link function to use for ordinal and hierarchical models, specified as the comma-separated pair consisting of 'Link' and one of the following.

`'logit'`	Default. f(γ) = ln(γ/(1 –γ))
`'probit'`	f(γ) = Φ^-1(γ) — error term is normally distributed with variance 1
`'comploglog'`	Complementary log-log f(γ) = ln(–ln(1 – γ))
`'loglog'`	f(γ) = ln(–ln(γ))

The link function defines the relationship between response probabilities and the linear combination of predictors, Xβ. The link functions might be functions of cumulative or conditional probabilities based on whether the model is for an ordinal or a sequential/nested response. For example, for an ordinal model, γ represents the cumulative probability of being in categories 1 to j and the model with a logit link function as follows:

$\ln (\frac{γ}{1 - γ}) = \ln (\frac{π_{1} + π_{2} + \dots + π_{j}}{π_{j + 1} + \dots + π_{k}}) = β_{0 j} + β_{1} X_{1} + β_{2} X_{2} + \dots + β_{p} X_{p},$

where k represents the last category.

You cannot specify the 'Link' parameter for nominal models; these always use a multinomial logit link,

$\ln (\frac{π_{j}}{π_{r}}) = β_{j 0} + β_{j 1} X_{j 1} + β_{j 2} X_{j 2} + \dots + β_{j p} X_{j p}, j = 1, \dots, k - 1,$

where π stands for a categorical probability, and r corresponds to the reference category. mnrfit uses the last category as the reference category for nominal models.

Example: 'Link','loglog'

`EstDisp` — Indicator for estimating dispersion parameter
`'off'` (default) | `'on'`

Indicator for estimating a dispersion parameter, specified as the comma-separated pair consisting of 'EstDisp' and one of the following.

`'off'`	Default. Use the theoretical dispersion value of 1.
`'on'`	Estimate a dispersion parameter for the multinomial distribution in computing standard errors.

Example: 'EstDisp','on'

`Tolerance` — Termination tolerance
`1e-6` (default) | numeric scalar

Termination tolerance for the Iteratively Reweighted Least Squares (IRLS) fitting algorithm, specified as a numeric scalar. If the relative difference of each coefficient is less than Tolerance across two iterations of the IRLS algorithm, then mnrfit considers the model to be converged. The default value for Tolerance is 1e-6.

For more information about the IRLS algorithm, see Iteratively Reweighted Least Squares.

Example: Tolerance=1e-4

Data Types: single | double

`Weights` — Observation weights
n-by-1 vector of ones (default) | n-by-1 numeric vector

Observation weights, specified as an n-by-1 numeric vector, where n is the number of observations. The default value for Weights is an n-by-1 vector of ones.

Data Types: single | double

Output Arguments

collapse all

`B` — Coefficient estimates
vector | matrix

Coefficient estimates for a multinomial logistic regression of the responses in Y, returned as a vector or a matrix.

If 'Interaction' is 'off', then B is a k – 1 + p vector. The first k – 1 rows of B correspond to the intercept terms, one for each k – 1 multinomial categories, and the remaining p rows correspond to the predictor coefficients, which are common for all of the first k – 1 categories.
If 'Interaction' is 'on', then B is a (p + 1)-by-(k – 1) matrix. Each column of B corresponds to the estimated intercept term and predictor coefficients, one for each of the first k – 1 multinomial categories.

The estimates for the kth category are taken to be zero as mnrfit takes the last category as the reference category.

`dev` — Deviance of the fit
scalar value

Deviance of the fit, returned as a scalar value. It is twice the difference between the maximum achievable log likelihood and that attained under the fitted model. This corresponds to the sum of deviance residuals,

$d e v = 2 * \sum_{i}^{n} \sum_{j}^{k} y_{i j} * \log (\frac{y_{i j}}{{\hat{π}}_{i j} * m_{i}}) = \sum_{i}^{n} r d_{i},$

where rd_i are the deviance residuals. For deviance residuals see stats.

`stats` — Model statistics
structure

Model statistics, returned as a structure that contains the following fields.

`beta`	The coefficient estimates. These are the same as `B`.
`dfe`	Degrees of freedom for error If `'Interactions'` is `'off'`, then degrees of freedom is n(k – 1) – (k – 1 + p). If `'Interactions'` is `'on'`, then degrees of freedom is (n – p + 1)(k – 1).
`sfit`	Estimated dispersion parameter.
`s`	Theoretical or estimated dispersion parameter. If `'Estdisp'` is `'off'`, then `s` is the theoretical dispersion parameter, 1. If `'Estdisp'` is `'on'`, then `s` is equal to the estimated dispersion parameter, `sfit`.
`estdisp`	Indicator for a theoretical or estimated dispersion parameter.
`se`	Standard errors of coefficient estimates, `B`.
`coeffcorr`	Estimated correlation matrix for `B`.
`covb`	Estimated covariance matrix for `B`.
`t`	t statistics for `B`.
`p`	p-values for `B`.
`resid`	Raw residuals. Observed minus fitted values, $r_{i j} = y_{i j} - {\hat{π}}_{i j} * m_{i}, {\begin{matrix} i = 1, \dots, n \\ j = 1, \dots, k \end{matrix},$ where π_ij is the categorical, cumulative or conditional probability, and m_i is the corresponding sample size.
`residp`	Pearson residuals, which are the raw residuals scaled by the estimated standard deviation: $r p_{i j} = \frac{r_{i j}}{{\hat{σ}}_{i j}} = \frac{y_{i j} - {\hat{π}}_{i j} * m_{i}}{\sqrt{{\hat{π}}_{i j} * (1 - {\hat{π}}_{i j}) * m_{i}}}, {\begin{matrix} i = 1, \dots, n \\ j = 1, \dots, k \end{matrix},$ where π_ij is the categorical, cumulative, or conditional probability, and m_i is the corresponding sample size.
`residd`	Deviance residuals: $r d_{i} = 2 * \sum_{j}^{k} y_{i j} * \log (\frac{y_{i j}}{{\hat{π}}_{i j} * m_{i}}), i = 1, \dots, n .$ where π_ij is the categorical, cumulative, or conditional probability, and m_i is the corresponding sample size.

Algorithms

mnrfit treats NaNs in either X or Y as missing values, and ignores them.

References

[1] McCullagh, P., and J. A. Nelder. Generalized Linear Models. New York: Chapman & Hall, 1990.

[2] Long, J. S. Regression Models for Categorical and Limited Dependent Variables. Sage Publications, 1997.

[3] Dobson, A. J., and A. G. Barnett. An Introduction to Generalized Linear Models. Chapman and Hall/CRC. Taylor & Francis Group, 2008.

Version History

Introduced in R2006b

collapse all

R2023b: `mnrfit` is not recommended

mnrfit is not recommended. Use fitmnr instead. There are no plans to remove mnrfit.

Starting in R2023b, use the fitmnr function to fit a MultinomialRegression model object. The fitmnr function has these advantages over the mnrfit function:

Table support for predictor and response input arguments
Option to specify predictors as categorical
Option to specify observation weights
MultinomialRegression object with output has properties that contain:
- Fitted response values
- Loglikelihood of the fitted model
- Criterion for model comparison
- Pseudo R-squared values for the fitted model
For a complete list of MultinomialRegression object properties, see MultinomialRegression.

mnrfit

Syntax

Description

Examples

Multinomial Regression for Nominal Responses

Multinomial Regression for Ordinal Responses

Hierarchical Multinomial Regression Model

Input Arguments

`X` — Observations on predictor variables
n-by-p matrix

`Y` — Response category labels
n-by-k matrix | n-by-1 numeric vector | n-by-1 logical vector | n-by-1 string vector | n-by-1 categorical array | n-by-1 cell array of character vectors

Name-Value Arguments

`Model` — Type of model to fit
`'nominal'` (default) | `'ordinal'` | `'hierarchical'`

`Interactions` — Indicator for interaction between multinomial categories and coefficients
`'on'` | `'off'`

`IterationLimit` — Maximum number of iterations
100 (default) | positive integer

`Link` — Link function
`'logit'` (default) | `'probit'` | `'comploglog'` | `'loglog'`

`EstDisp` — Indicator for estimating dispersion parameter
`'off'` (default) | `'on'`

`Tolerance` — Termination tolerance
`1e-6` (default) | numeric scalar

`Weights` — Observation weights
n-by-1 vector of ones (default) | n-by-1 numeric vector

Output Arguments

`B` — Coefficient estimates
vector | matrix

`dev` — Deviance of the fit
scalar value

`stats` — Model statistics
structure

Algorithms

References

Version History

R2023b: `mnrfit` is not recommended

See Also

Topics

mnrfit

Syntax

Description

Examples

Multinomial Regression for Nominal Responses

Multinomial Regression for Ordinal Responses

Hierarchical Multinomial Regression Model

Input Arguments

X — Observations on predictor variables n-by-p matrix

Y — Response category labels n-by-k matrix | n-by-1 numeric vector | n-by-1 logical vector | n-by-1 string vector | n-by-1 categorical array | n-by-1 cell array of character vectors

Name-Value Arguments

Model — Type of model to fit 'nominal' (default) | 'ordinal' | 'hierarchical'

Interactions — Indicator for interaction between multinomial categories and coefficients 'on' | 'off'

IterationLimit — Maximum number of iterations 100 (default) | positive integer

Link — Link function 'logit' (default) | 'probit' | 'comploglog' | 'loglog'

EstDisp — Indicator for estimating dispersion parameter 'off' (default) | 'on'

Tolerance — Termination tolerance 1e-6 (default) | numeric scalar

Weights — Observation weights n-by-1 vector of ones (default) | n-by-1 numeric vector

Output Arguments

B — Coefficient estimates vector | matrix

dev — Deviance of the fit scalar value

stats — Model statistics structure

Algorithms

References

Version History

R2023b: mnrfit is not recommended

See Also

Topics

`X` — Observations on predictor variables
n-by-p matrix

`Y` — Response category labels
n-by-k matrix | n-by-1 numeric vector | n-by-1 logical vector | n-by-1 string vector | n-by-1 categorical array | n-by-1 cell array of character vectors

`Model` — Type of model to fit
`'nominal'` (default) | `'ordinal'` | `'hierarchical'`

`Interactions` — Indicator for interaction between multinomial categories and coefficients
`'on'` | `'off'`

`IterationLimit` — Maximum number of iterations
100 (default) | positive integer

`Link` — Link function
`'logit'` (default) | `'probit'` | `'comploglog'` | `'loglog'`

`EstDisp` — Indicator for estimating dispersion parameter
`'off'` (default) | `'on'`

`Tolerance` — Termination tolerance
`1e-6` (default) | numeric scalar

`Weights` — Observation weights
n-by-1 vector of ones (default) | n-by-1 numeric vector

`B` — Coefficient estimates
vector | matrix

`dev` — Deviance of the fit
scalar value

`stats` — Model statistics
structure

R2023b: `mnrfit` is not recommended