What Are Parametric Nonlinear Regression Models?

Parametric nonlinear models represent the relationship between a continuous response variable and one or more continuous predictor variables in the form

where

In contrast, nonparametric models do not attempt to characterize the relationship between predictors and response with model parameters. Descriptions are often graphical, as in the case of Decision Trees.

fitnlm attempts to find values of the parameters β that minimize the mean squared differences between the observed responses y and the predictions of the model f(X,β). To do so, it needs a starting value beta0 before iteratively modifying the vector β to a vector with minimal mean squared error.

Prepare Data

To begin fitting a regression, put your data into a form that fitting functions expect. All regression techniques begin with input data in an array X and response data in a separate vector y, or input data in a table or dataset array tbl and response data as a column in tbl. Each row of the input data represents one observation. Each column represents one predictor (variable).

For a table or dataset array tbl, indicate the response variable with the 'ResponseVar' name-value pair:

mdl = fitlm(tbl,'ResponseVar','BloodPressure');

The response variable is the last column by default.

You cannot use categorical predictors for nonlinear regression. A categorical predictor is one that takes values from a fixed set of possibilities.

Represent missing data as NaN for both input data and response data.

ds = dataset('XLSFile','hospital.xls',...
    'ReadObsNames',true);

load carsmall
ds = dataset(Weight,Model_Year,MPG);

tbl = readtable('hospital.xls',...
    'ReadRowNames',true);

load carsmall
tbl = table(Weight,Model_Year,MPG);

load carsmall
X = [Weight Horsepower Cylinders Model_Year];
y = MPG;

[X, Xnames] = xlsread('hospital.xls');
y = X(:,4); % response y is systolic pressure
X(:,4) = []; % remove y from the X matrix

Represent the Nonlinear Model

There are several ways to represent a nonlinear model. Use whichever is most convenient.

The nonlinear model is a required input to fitnlm, in the modelfun input.

fitnlm assumes that the response function f(X,β) is smooth in the parameters β. If your function is not smooth, fitnlm can fail to provide optimal parameter estimates.

• Function Handle to Anonymous Function or Function File

• Text Representation of Formula

function yhat = hougen(beta,x)
%HOUGEN Hougen-Watson model for reaction kinetics.
%   YHAT = HOUGEN(BETA,X) gives the predicted values of the
%   reaction rate, YHAT, as a function of the vector of 
%   parameters, BETA, and the matrix of data, X.
%   BETA must have 5 elements and X must have three
%   columns.
%
%   The model form is:
%   y = (b1*x2 - x3/b5)./(1+b2*x1+b3*x2+b4*x3)
%
%   Reference:
%      [1]  Bates, Douglas, and Watts, Donald, "Nonlinear
%      Regression Analysis and Its Applications", Wiley
%      1988 p. 271-272.

%   Copyright 1993-2004 The MathWorks, Inc. 
%   B.A. Jones 1-06-95.

b1 = beta(1);
b2 = beta(2);
b3 = beta(3);
b4 = beta(4);
b5 = beta(5);

x1 = x(:,1);
x2 = x(:,2);
x3 = x(:,3);

yhat = (b1*x2 - x3/b5)./(1+b2*x1+b3*x2+b4*x3);

modelfun = @(b,x)(b(1)*x(:,2) - x(:,3)/b(5))./...
(1 + b(2)*x(:,1) + b(3)*x(:,2) + b(4)*x(:,3));

modelfun = 'y ~ (b1*x2 - x3/b5)/(1 + b2*x1 + b3*x2 + b4*x3)';

Choose Initial Vector beta0

The initial vector for the fitting iterations, beta0, can greatly influence the quality of the resulting fitted model. beta0 gives the dimensionality of the problem, meaning it needs the correct length. A good choice of beta0 leads to a quick, reliable model, while a poor choice can lead to a long computation, or to an inadequate model.

It is difficult to give advice on choosing a good beta0. If you believe certain components of the vector should be positive or negative, set your beta0 to have those characteristics. If you know the approximate value of other components, include them in beta0. However, if you don’t know good values, try a random vector, such as

beta0 = randn(nVars,1);
% or
beta0 = 10*rand(nVars,1);

Fit Nonlinear Model to Data

The syntax for fitting a nonlinear regression model using a table or dataset array tbl is

mdl = fitnlm(tbl,modelfun,beta0)

The syntax for fitting a nonlinear regression model using a numeric array X and numeric response vector y is

mdl = fitnlm(X,y,modelfun,beta0)

For information on representing the input parameters, see Prepare Data, Represent the Nonlinear Model, and Choose Initial Vector beta0.

fitnlm assumes that the response variable in a table or dataset array tbl is the last column. To change this, use the ResponseVar name-value pair to name the response column.

Examine Quality and Adjust the Fitted Nonlinear Model

There are diagnostic plots to help you examine the quality of a model. plotDiagnostics(mdl) gives a variety of plots, including leverage and Cook's distance plots. plotResiduals(mdl) gives the difference between the fitted model and the data.

There are also properties of mdl that relate to the model quality. mdl.RMSE gives the root mean square error between the data and the fitted model. mdl.Residuals.Raw gives the raw residuals. mdl.Diagnostics contains several fields, such as Leverage and CooksDistance, that can help you identify particularly interesting observations.

This example shows how to examine a fitted nonlinear model using diagnostic, residual, and slice plots.

Load the sample data.

load reaction

Create a nonlinear model of rate as a function of reactants using the hougen.m function.

beta0 = ones(5,1);
mdl = fitnlm(reactants,...
    rate,@hougen,beta0);

Make a leverage plot of the data and model.

plotDiagnostics(mdl)

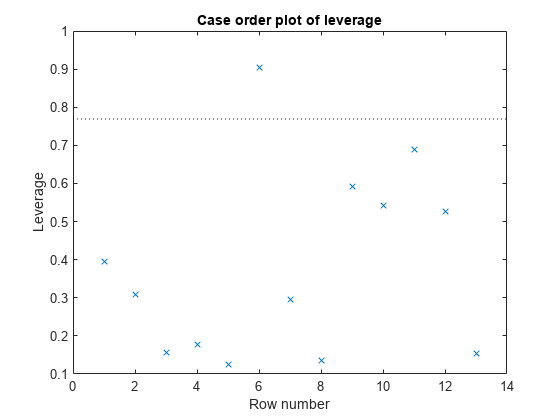
There is one point that has high leverage. Locate the point.

[~,maxl] = max(mdl.Diagnostics.Leverage)

maxl = 
6

Examine a residuals plot.

plotResiduals(mdl,'fitted')

Nothing stands out as an outlier.

Use a slice plot to show the effect of each predictor on the model.

plotSlice(mdl)

You can drag the vertical dashed blue lines to see the effect of a change in one predictor on the response. For example, drag the X2 line to the right, and notice that the slope of the X3 line changes.

Predict or Simulate Responses Using a Nonlinear Model

This example shows how to use the methods predict, feval, and random to predict and simulate responses to new data.

Randomly generate a sample from a Cauchy distribution.

rng('default')
X = rand(100,1);
X = tan(pi*X - pi/2);

Generate the response according to the model y = b1*(pi /2 + atan((x - b2) / b3)) and add noise to the response.

modelfun = @(b,x) b(1) * ...
    (pi/2 + atan((x - b(2))/b(3)));
y = modelfun([12 5 10],X) + randn(100,1);

Fit a model starting from the arbitrary parameters b = [1,1,1].

beta0 = [1 1 1]; % An arbitrary guess
mdl = fitnlm(X,y,modelfun,beta0)

mdl = 
Nonlinear regression model:
    y ~ b1*(pi/2 + atan((x - b2)/b3))

Estimated Coefficients:
          Estimate      SE       tStat       pValue  
          ________    _______    ______    __________

    b1     12.082     0.80028    15.097    3.3151e-27
    b2     5.0603      1.0825    4.6747    9.5063e-06
    b3       9.64     0.46499    20.732    2.0382e-37


Number of observations: 100, Error degrees of freedom: 97
Root Mean Squared Error: 1.02
R-Squared: 0.92,  Adjusted R-Squared 0.918
F-statistic vs. zero model: 6.45e+03, p-value = 1.72e-111

The fitted values are within a few percent of the parameters [12,5,10].

Examine the fit.

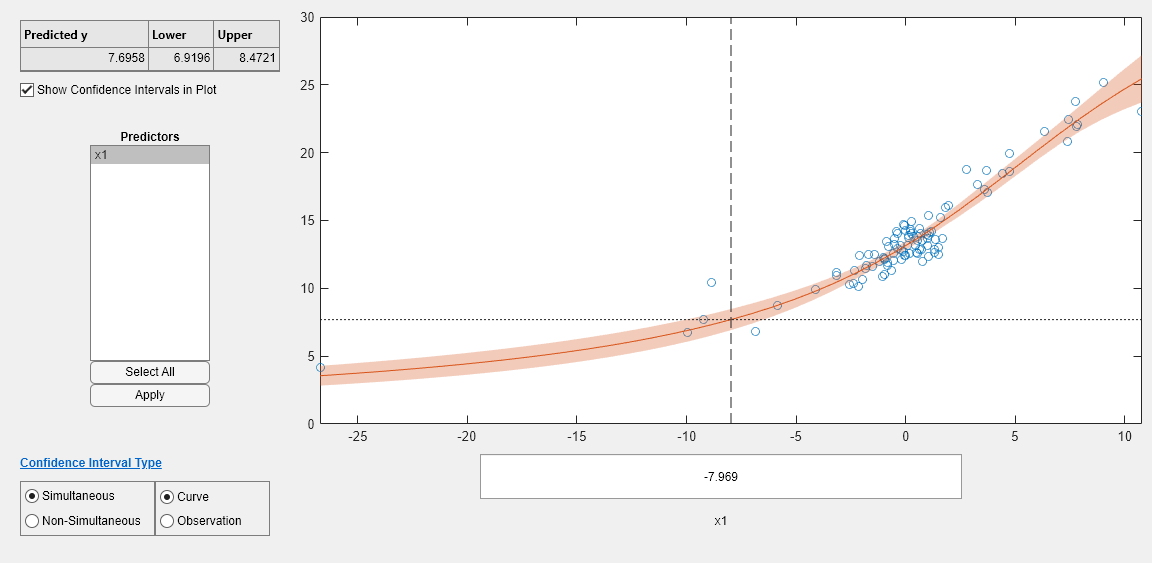
plotSlice(mdl)

Xnew = [-15;5;12];
[ynew,ynewci] = predict(mdl,Xnew)

ynew = 3×1

    5.4122
   18.9022
   26.5161

ynewci = 3×2

    4.8233    6.0010
   18.4555   19.3490
   25.0170   28.0151

ds = dataset({X,'X'},{y,'y'});
mdl2 = fitnlm(ds,modelfun,beta0);

Xnew = [-15;5;12];
ynew = feval(mdl2,Xnew)

ynew = 3×1

    5.4122
   18.9022
   26.5161

Xnew = [-15;5;12];
ysim = random(mdl,Xnew)

ysim = 3×1

    6.0505
   19.0893
   25.4647

ysim = random(mdl,Xnew)

ysim = 3×1

    6.3813
   19.2157
   26.6541