predict

Fit a quantile neural network regression model using the 0.25, 0.50, and 0.75 quantiles.

Load the carbig data set, which contains measurements of cars made in the 1970s and early 1980s. Create a matrix X containing the predictor variables Acceleration, Displacement, Horsepower, and Weight. Store the response variable MPG in the variable Y.

load carbig
X = [Acceleration,Displacement,Horsepower,Weight];
Y = MPG;

Delete rows of X and Y where either array has missing values.

R = rmmissing([X Y]);
X = R(:,1:end-1);
Y = R(:,end);

Partition the data into training data (XTrain and YTrain) and test data (XTest and YTest). Reserve approximately 20% of the observations for testing, and use the rest of the observations for training.

rng(0,"twister") % For reproducibility of the partition
c = cvpartition(length(Y),"Holdout",0.20);
 
trainingIdx = training(c);
XTrain = X(trainingIdx,:);
YTrain = Y(trainingIdx);
 
testIdx = test(c);
XTest = X(testIdx,:);
YTest = Y(testIdx);

Train a quantile neural network regression model. Specify to use the 0.25, 0.50, and 0.75 quantiles (that is, the lower quartile, median, and upper quartile). To improve the model fit, standardize the numeric predictors. Use a ridge (L2) regularization term of 1. Adding a regularization term can help prevent quantile crossing.

Mdl = fitrqnet(XTrain,YTrain,Quantiles=[0.25,0.50,0.75], ...
    Standardize=true,Lambda=0.05)

Mdl = 
  RegressionQuantileNeuralNetwork
             ResponseName: 'Y'
    CategoricalPredictors: []
               LayerSizes: 10
              Activations: 'relu'
    OutputLayerActivation: 'none'
                Quantiles: [0.2500 0.5000 0.7500]

Mdl is a RegressionQuantileNeuralNetwork model object. You can use dot notation to access the properties of Mdl. For example, Mdl.LayerWeights and Mdl.LayerBiases contain the weights and biases, respectively, for the fully connected layers of the trained model.

In this example, you can use the layer weights, layer biases, predictor means, and predictor standard deviations directly to predict the test set responses for each of the three quantiles in Mdl.Quantiles. In general, you can use the predict object function to make quantile predictions.

firstFCStep = (Mdl.LayerWeights{1})*((XTest-Mdl.Mu)./Mdl.Sigma)' ...
    + Mdl.LayerBiases{1};
reluStep = max(firstFCStep,0);
finalFCStep = (Mdl.LayerWeights{end})*reluStep + Mdl.LayerBiases{end};
predictedY = finalFCStep'

predictedY = 78×3

   13.9602   15.1340   16.6884
   11.2792   12.2332   13.4849
   19.5525   21.7303   23.9473
   22.6950   25.5260   28.1201
   10.4533   11.3377   12.4984
   17.6935   19.5194   21.5152
   12.4312   13.4797   14.8614
   11.7998   12.7963   14.1071
   16.6860   18.3305   20.2070
   24.1142   27.0301   29.7811
      ⋮

isequal(predictedY,predict(Mdl,XTest))

ans = logical
   1

Each column of predictedY corresponds to a separate quantile (0.25, 0.5, or 0.75).

Visualize the predictions of the quantile neural network regression model. First, create a grid of predictor values.

minX = floor(min(X))

minX = 1×4

           8          68          46        1613

maxX = ceil(max(X))

maxX = 1×4

          25         455         230        5140

gridX = zeros(100,size(X,2));
for p = 1:size(X,2)
    gridp = linspace(minX(p),maxX(p))';
    gridX(:,p) = gridp;
end

Next, use the trained model Mdl to predict the response values for the grid of predictor values.

gridY = predict(Mdl,gridX)

gridY = 100×3

   31.2419   35.0661   38.6357
   30.8637   34.6317   38.1573
   30.4854   34.1972   37.6789
   30.1072   33.7627   37.2005
   29.7290   33.3283   36.7221
   29.3507   32.8938   36.2436
   28.9725   32.4593   35.7652
   28.5943   32.0249   35.2868
   28.2160   31.5904   34.8084
   27.8378   31.1560   34.3300
      ⋮

For each observation in gridX, the predict object function returns predictions for the quantiles in Mdl.Quantiles.

View the gridY predictions for the second predictor (Displacement). Compare the quantile predictions to the true test data values.

predictorIdx = 2;
plot(XTest(:,predictorIdx),YTest,".")
hold on
plot(gridX(:,predictorIdx),gridY(:,1))
plot(gridX(:,predictorIdx),gridY(:,2))
plot(gridX(:,predictorIdx),gridY(:,3))
hold off
xlabel("Predictor (Displacement)")
ylabel("Response (MPG)")
legend(["True values","0.25 predicted values", ...
    "0.50 predicted values","0.75 predicted values"])
title("Test Data")

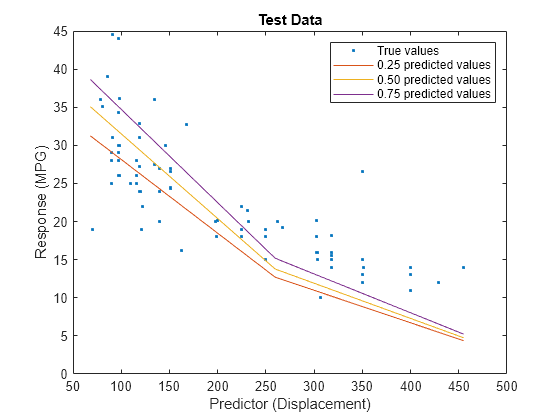
The red curve shows the predictions for the 0.25 quantile, the yellow curve shows the predictions for the 0.50 quantile, and the purple curve shows the predictions for the 0.75 quantile. The blue points indicate the true test data values.

Notice that the quantile prediction curves do not cross each other.

When training a quantile neural network regression model, you can use a ridge (L2) regularization term to prevent quantile crossing.

Load the carbig data set, which contains measurements of cars made in the 1970s and early 1980s. Create a table containing the predictor variables Acceleration, Cylinders, Displacement, and so on, as well as the response variable MPG.

load carbig
cars = table(Acceleration,Cylinders,Displacement, ...
    Horsepower,Model_Year,Origin,Weight,MPG);

Remove rows of cars where the table has missing values.

cars = rmmissing(cars);

Categorize the cars based on whether they were made in the USA.

cars.Origin = categorical(cellstr(cars.Origin));
cars.Origin = mergecats(cars.Origin,["France","Japan",...
    "Germany","Sweden","Italy","England"],"NotUSA");

Partition the data into training and test sets using cvpartition. Use approximately 80% of the observations as training data, and 20% of the observations as test data.

rng(0,"twister") % For reproducibility of the data partition
c = cvpartition(height(cars),"Holdout",0.20);

trainingIdx = training(c);
carsTrain = cars(trainingIdx,:);

testIdx = test(c);
carsTest = cars(testIdx,:);

Train a quantile neural network regression model. Use the 0.25, 0.50, and 0.75 quantiles (that is, the lower quartile, median, and upper quartile). To improve the model fit, standardize the numeric predictors before training.

Mdl = fitrqnet(carsTrain,"MPG",Quantiles=[0.25 0.5 0.75], ...
    Standardize=true);

Mdl is a RegressionNeuralNetwork model object.

Determine if the test data predictions for the quantiles in Mdl.Quantiles cross each other by using the predict object function of Mdl. The crossingIndicator output argument contains a value of 1 (true) for any observation with quantile predictions that cross.

[~,crossingIndicator] = predict(Mdl,carsTest);
sum(crossingIndicator)

ans = 
2

In this example, two of the observations in carsTest have quantile predictions that cross each other.

To prevent quantile crossing, specify the Lambda name-value argument in the call to fitrqnet. Use a 0.05 ridge (L2) penalty term.

newMdl = fitrqnet(carsTrain,"MPG",Quantiles=[0.25 0.5 0.75], ...
    Standardize=true,Lambda=0.05);
[predictedY,newCrossingIndicator] = predict(newMdl,carsTest);
sum(newCrossingIndicator)

ans = 
0

With regularization, the predictions for the test data set do not cross for any observations.

Visualize the predictions returned by newMdl by using a scatter plot with a reference line. Plot the predicted values along the vertical axis and the true response values along the horizontal axis. Points on the reference line indicate correct predictions.

plot(carsTest.MPG,predictedY(:,1),".")
hold on
plot(carsTest.MPG,predictedY(:,2),".")
plot(carsTest.MPG,predictedY(:,3),".")
plot(carsTest.MPG,carsTest.MPG)
hold off
xlabel("True MPG")
ylabel("Predicted MPG")
legend(["0.25 quantile values","0.50 quantile values", ...
    "0.75 quantile values","Reference line"], ...
    Location="southeast")
title("Test Data")

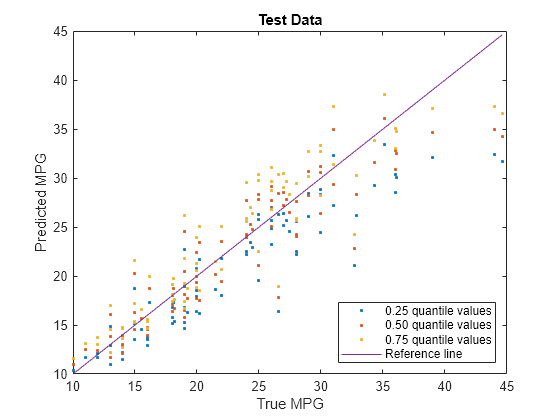
Blue points correspond to the 0.25 quantile, red points correspond to the 0.50 quantile, and yellow points correspond to the 0.75 quantile.