Explore Single-Period Asset Arbitrage

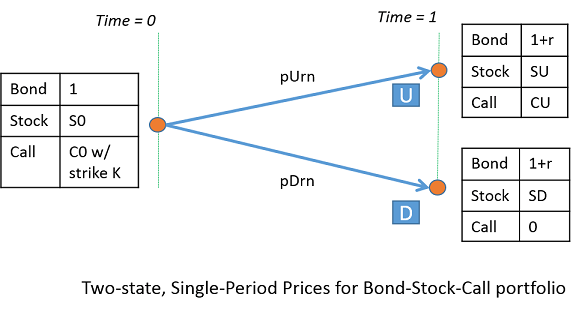
Define Parameters of the Portfolio

Create the symbolic variable r representing the risk-free rate over the period. Set the assumption that r is a positive value.

syms r positive

Define the parameters for the beginning of a single period, time = 0. Here S0 is the stock price, and C0 is the call option price with strike, K.

syms S0 C0 K positive

Now, define the parameters for the end of a period, time = 1. Label the two possible states at the end of the period as U (the stock price over this period goes up) and D (the stock price over this period goes down). Thus, SU and SD are the stock prices at states U and D, and CU is the value of the call at state U. Note that $$SD<=K<=SU$$.

syms SU SD CU positive

The bond price at time = 0 is 1. Note that this example ignores friction costs.

Collect the prices at time = 0 into a column vector.

prices = [1 S0 C0]'

prices = 
$$\left(\begin{array}{c}1\\ S_0\\ C_0\end{array}\right)$$

Collect the payoffs of the portfolio at time = 1 into the payoff matrix. The columns of payoff correspond to payoffs for states D and U. The rows correspond to payoffs for bond, stock, and call. The payoff for the bond is 1 + r. The payoff for the call in state D is zero since it is not exercised (because $$SD<=K$$).

payoff = [(1 + r), (1 + r); SD, SU; 0, CU]

payoff = 
$$\left(\begin{array}{cc}r+1& r+1\\ \mathrm{SD}& \mathrm{SU}\\ 0& \mathrm{CU}\end{array}\right)$$

CU is worth SU - K in state U. Substitute this value in payoff.

payoff = subs(payoff, CU, SU - K)

payoff = 
$$\left(\begin{array}{cc}r+1& r+1\\ \mathrm{SD}& \mathrm{SU}\\ 0& \mathrm{SU}-K\end{array}\right)$$

Solve for Risk-Neutral Probabilities

Define the probabilities of reaching states U and D.

syms pU pD real

Under no-arbitrage, eqns == 0 must always hold true with positive pU and pD.

eqns = payoff*[pD; pU] - prices

eqns = 
$$\left(\begin{array}{c}\mathrm{pD}\hspace{0.17em}\left(r+1\right)+\mathrm{pU}\hspace{0.17em}\left(r+1\right)-1\\ \mathrm{SD}\hspace{0.17em}\mathrm{pD}-S_0+\mathrm{SU}\hspace{0.17em}\mathrm{pU}\\ -C_0-\mathrm{pU}\hspace{0.17em}\left(K-\mathrm{SU}\right)\end{array}\right)$$

Transform equations to use risk-neutral probabilities.

syms pDrn pUrn real;
eqns = subs(eqns, [pD; pU], [pDrn; pUrn]/(1 + r))

eqns = 
$$\left(\begin{array}{c}\mathrm{pDrn}+\mathrm{pUrn}-1\\ \frac{\mathrm{SD}\hspace{0.17em}\mathrm{pDrn}}{r+1}-S_0+\frac{\mathrm{SU}\hspace{0.17em}\mathrm{pUrn}}{r+1}\\ -C_0-\frac{\mathrm{pUrn}\hspace{0.17em}\left(K-\mathrm{SU}\right)}{r+1}\end{array}\right)$$

The unknown variables are pDrn, pUrn, and C0. Transform the linear system to a matrix form using these unknown variables.

[A, b] = equationsToMatrix(eqns, [pDrn, pUrn, C0]')

A = 
$$\left(\begin{array}{ccc}1& 1& 0\\ \frac{\mathrm{SD}}{r+1}& \frac{\mathrm{SU}}{r+1}& 0\\ 0& -\frac{K-\mathrm{SU}}{r+1}& -1\end{array}\right)$$

b = 
$$\left(\begin{array}{c}1\\ S_0\\ 0\end{array}\right)$$

Using linsolve, find the solution for the risk-neutral probabilities and call price.

x = linsolve(A, b)

x = 
$$\left(\begin{array}{c}\frac{S_0-\mathrm{SU}+S_0\hspace{0.17em}r}{\mathrm{SD}-\mathrm{SU}}\\ -\frac{S_0-\mathrm{SD}+S_0\hspace{0.17em}r}{\mathrm{SD}-\mathrm{SU}}\\ \frac{\left(K-\mathrm{SU}\right)\hspace{0.17em}\left(S_0-\mathrm{SD}+S_0\hspace{0.17em}r\right)}{\left(\mathrm{SD}-\mathrm{SU}\right)\hspace{0.17em}\left(r+1\right)}\end{array}\right)$$

Verify the Solution

Verify that under risk-neutral probabilities, x(1:2), the expected rate of return for the portfolio, E_return equals the risk-free rate, r.

E_return = diag(prices)\(payoff - [prices,prices])*x(1:2);
E_return = simplify(subs(E_return, C0, x(3)))

E_return = 
$$\left(\begin{array}{c}r\\ r\\ r\end{array}\right)$$

Test for No-Arbitrage Violations

As an example of testing no-arbitrage violations, use the following values: r = 5%, S0 = 100, and K = 100. For SU < 105, the no-arbitrage condition is violated because pDrn = xSol(1) is negative (SU >= SD). Further, for any call price other than xSol(3), there is arbitrage.

xSol = simplify(subs(x, [r,S0,K], [0.05,100,100]))

xSol = 
$$\left(\begin{array}{c}-\frac{\mathrm{SU}-105}{\mathrm{SD}-\mathrm{SU}}\\ \frac{\mathrm{SD}-105}{\mathrm{SD}-\mathrm{SU}}\\ \frac{20\hspace{0.17em}\left(\mathrm{SD}-105\right)\hspace{0.17em}\left(\mathrm{SU}-100\right)}{21\hspace{0.17em}\left(\mathrm{SD}-\mathrm{SU}\right)}\end{array}\right)$$

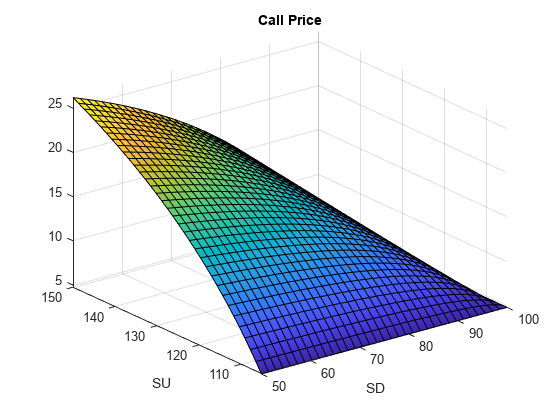
Plot Call Price as a Surface

Plot the call price, C0 = xSol(3), for 50 <= SD <= 100 and 105 <= SU <= 150. Note that the call is worth more when the "variance" of the underlying stock price is higher for example, SD = 50, SU = 150.

fsurf(xSol(3), [50,100,105,150])
xlabel SD
ylabel SU
title 'Call Price'

Reference

Advanced Derivatives, Pricing and Risk Management: Theory, Tools and Programming Applications by Albanese, C., Campolieti, G.