lambertw

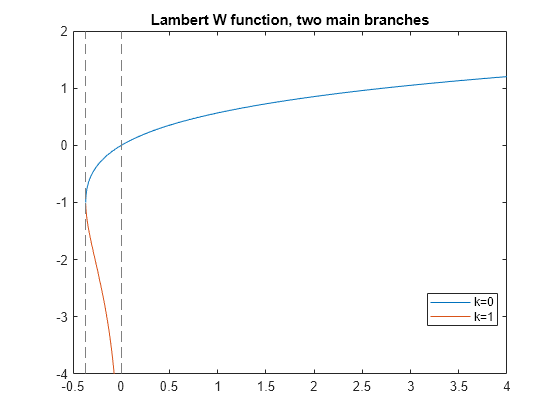
Lambert W function

collapse all in page

Syntax

lambertw(x)
lambertw(k,x)

Description

lambertw(x) returns the principal branch of the Lambert W function. This syntax is equivalent to lambertw(0,x).

example

lambertw(k,x) is the kth branch of the Lambert W function. This syntax returns real values only if k = 0 or k = -1.

example

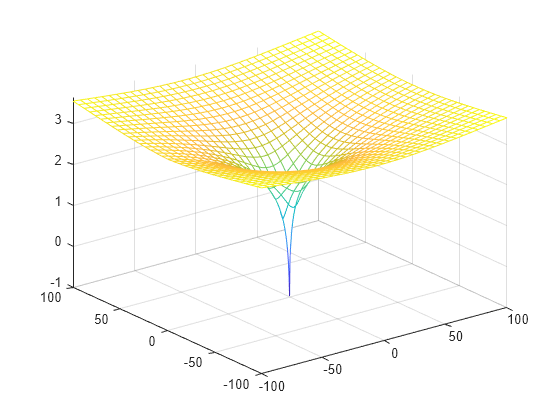
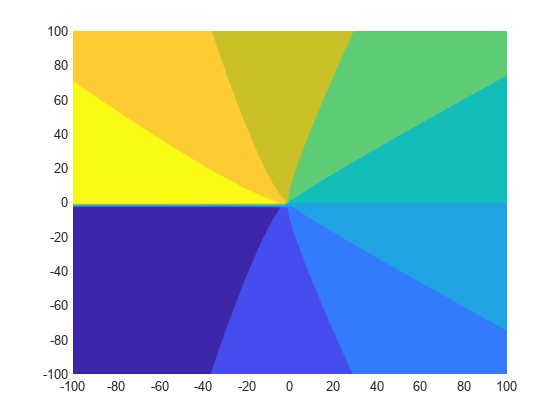
Examples

collapse all

The Lambert W function W(x) is a set of solutions of the equation x = W(x)eW(x).

Solve this equation. The solution is the Lambert W function.

syms x W
eqn = x == W*exp(W);
solve(eqn,W)
ans =
lambertw(0, x)

Verify that branches of the Lambert W function are valid solutions of the equation x = W*eW:

k = -2:2;
eqn = subs(eqn,W,lambertw(k,x));
isAlways(eqn)
ans =
  1×5 logical array
     1     1     1     1     1

Depending on its arguments, lambertw can return floating-point or exact symbolic results.

Compute the Lambert W functions for these numbers. Because the numbers are not symbolic objects, you get floating-point results.

A = [0 -1/exp(1); pi i];
lambertw(A)
ans =
   0.0000 + 0.0000i  -1.0000 + 0.0000i
   1.0737 + 0.0000i   0.3747 + 0.5764i

lambertw(-1,A)
ans =
     -Inf + 0.0000i  -1.0000 + 0.0000i
  -0.3910 - 4.6281i  -1.0896 - 2.7664i

Compute the Lambert W functions for the numbers converted to symbolic objects. For most symbolic (exact) numbers, lambertw returns unresolved symbolic calls.

A = [0 -1/exp(sym(1)); pi i];
W0 = lambertw(A)
W0 =
[               0,             -1]
[ lambertw(0, pi), lambertw(0, 1i)]

Wmin1 = lambertw(-1,A)
Wmin1 =
[             -Inf,              -1]
[ lambertw(-1, pi), lambertw(-1, 1i)]

Convert symbolic results to double by using double.

double(W0)
ans =
   0.0000 + 0.0000i  -1.0000 + 0.0000i
   1.0737 + 0.0000i   0.3747 + 0.5764i
Open Live Script

Plot the two main branches, W0(x) and W-1(x), of the Lambert W function.

syms x
fplot(lambertw(x))
hold on
fplot(lambertw(-1,x))
hold off
axis([-0.5 4 -4 2])
title('Lambert W function, two main branches')
legend('k=0','k=1','Location','best')

Figure contains an axes object. The axes object with title Lambert W function, two main branches contains 2 objects of type functionline. These objects represent k=0, k=1.

Open Live Script

Plot the principal branch of the Lambert W function on the complex plane.

Plot the real value of the Lambert W function by using fmesh. Simultaneously plot the contours by setting 'ShowContours' to 'On'.

syms x y
f = lambertw(x + 1i*y);
interval = [-100 100 -100 100];
fmesh(real(f),interval,'ShowContours','On')

Figure contains an axes object. The axes object contains an object of type functionsurface.

Plot the imaginary value of the Lambert W function. The plot has a branch cut along the negative real axis. Plot the contours separately.

fmesh(imag(f),interval)

Figure contains an axes object. The axes object contains an object of type functionsurface.

fcontour(imag(f),interval,'Fill','on')

Figure contains an axes object. The axes object contains an object of type functioncontour.

Plot the absolute value of the Lambert W function.

fmesh(abs(f),interval,'ShowContours','On')

Figure contains an axes object. The axes object contains an object of type functionsurface.

Input Arguments

collapse all

Input, specified as a number, vector, matrix, or array, or a symbolic number, variable, array, function, or expression.

At least one input argument must be a scalar, or both arguments must be vectors or matrices of the same size. If one input argument is a scalar and the other is a vector or matrix, lambertw expands the scalar into a vector or matrix of the same size as the other argument with all elements equal to that scalar.

Branch of Lambert W function, specified as an integer, a vector or matrix of integers, a symbolic integer, or a symbolic vector or matrix of integers.

At least one input argument must be a scalar, or both arguments must be vectors or matrices of the same size. If one input argument is a scalar and the other is a vector or matrix, lambertw expands the scalar into a vector or matrix of the same size as the other argument with all elements equal to that scalar.

More About

collapse all

References

[1] Corless, R.M., G.H. Gonnet, D.E.G. Hare, D.J. Jeffrey, and D.E. Knuth. "On the Lambert W Function." Advances in Computational Mathematics, Vol. 5, pp. 329–359, 1996.

Version History

Introduced before R2006a

See Also

Functions