Transform Spherical Coordinates to Cartesian Coordinates and Plot Analytically

Open Live Script

This example shows how to transform a symbolic expression from spherical coordinates to Cartesian coordinates, and plot the converted expression analytically without explicitly generating numerical data.

In the spherical coordinate system, the location of a point $P$ can be characterized by three variables. Different textbooks have different conventions for the variables used to describe spherical coordinates. For these examples, this convention is used:

The radial distance $ρ$
The azimuthal angle $θ$
The polar angle $ϕ$

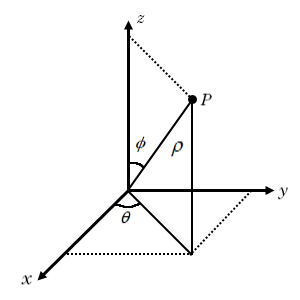
The transformation of the point $P$ from spherical coordinates $(ρ, θ, ϕ)$ to Cartesian coordinates $(x, y, z)$ is given by

$\begin{array}{l} x = ρ \sin ϕ \cos θ, \\ y = ρ \sin ϕ \sin θ, \\ z = ρ \cos ϕ . \end{array}$

By transforming symbolic expressions from spherical coordinates to Cartesian coordinates, you can then plot the expressions using Symbolic Math Toolbox™ graphics functions, such as fplot3 and fsurf.

Plot a Point and Its Projections

Plot the point $P$ that is located at $(ρ, θ, ϕ) = (1, 1.2, 0.75)$ .

Transform the spherical coordinates to Cartesian coordinates $(x_{P}, y_{P}, z_{P})$ . Because the converted coordinates contain numerical values, use plot3 to plot the point.

rho = 1;
theta = 1.2;
phi = 0.75;
x_P = rho*sin(phi)*cos(theta);
y_P = rho*sin(phi)*sin(theta);
z_P = rho*cos(phi);
plot3(x_P,y_P,z_P,'ko','MarkerSize',10,'MarkerFaceColor','k')
hold on

Label each axis in the plot, change the line of sight, and set the axis scaling to use equal data units.

xlabel('x')
ylabel('y')
zlabel('z')
view([75 40])
axis equal;

Next, plot the line projection of the point $P$ to the origin. This line projection in spherical coordinates is parameterized by $(r, 1.2, 0.75)$ , with $r$ ranging from $0$ to $1$ . Specify this line parameterization as symbolic expressions, and plot it by using fplot3.

syms r
xr = r*sin(phi)*cos(theta);
yr = r*sin(phi)*sin(theta);
zr = r*cos(phi);
fplot3(xr,yr,zr,[0 rho],'k')

Plot the vertical line projection to the $x y$ -plane. This line projection in Cartesian coordinates is parameterized by $(x_{P}, y_{P}, z)$ , with $z$ ranging from $0$ to $z_{P}$ .

syms z
fplot3(sym(x_P),sym(y_P),z,[0 z_P],'k')

Plot the top horizontal line projection to the $z$ -axis. This line projection in Cartesian coordinates is parameterized by $(r \sin ϕ \cos θ, r \sin ϕ \sin θ, z_{P})$ , with $r$ ranging from $0$ to $1$ .

fplot3(xr,yr,sym(z_P),[0 rho],'k--')

Plot the bottom horizontal line projection to the $z$ -axis. This line projection in Cartesian coordinates is parameterized by $(r \sin ϕ \cos θ, r \sin ϕ \sin θ, 0)$ , with $r$ ranging from $0$ to $1$ .

fplot3(xr,yr,sym(0),[0 rho],'k')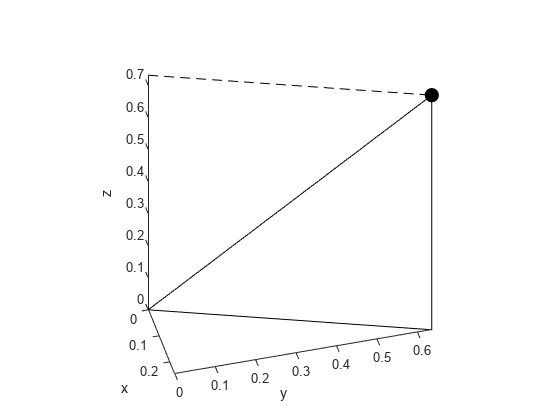

Figure contains an axes object. The axes object with xlabel x, ylabel y contains 5 objects of type line, parameterizedfunctionline. One or more of the lines displays its values using only markers

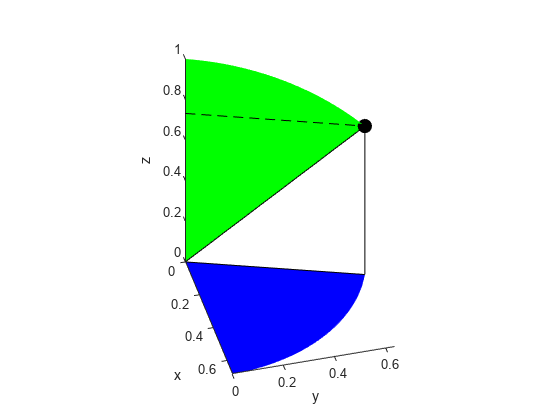
Next, plot the plane that shows the span of the azimuthal angle $θ$ in the $x y$ -plane with the coordinate $z = 0$ .

syms s t
x_azimuthal = s*sin(phi)*cos(t);
y_azimuthal = s*sin(phi)*sin(t);
fsurf(x_azimuthal,y_azimuthal,0,[0 rho 0 theta],'FaceColor','b','EdgeColor','none')

Plot the plane that shows the span of the polar angle $ϕ$ .

syms u v
x_polar = u*sin(v)*cos(theta);
y_polar = u*sin(v)*sin(theta);
z_polar = u*cos(v);
fsurf(x_polar,y_polar,z_polar,[0 rho 0 phi],'FaceColor','g','EdgeColor','none')
hold off

Figure contains an axes object. The axes object with xlabel x, ylabel y contains 7 objects of type line, parameterizedfunctionline, parameterizedfunctionsurface. One or more of the lines displays its values using only markers

Plot a Sphere

Plot a sphere with radius $r = 4$ .

In spherical coordinates, the sphere is parameterized by $(4, θ, ϕ)$ , with $ϕ$ ranging from $0$ to $π$ and $θ$ ranging from $0$ to $2 π$ . Transform spherical coordinates to Cartesian coordinates by specifying the surface parameterization as symbolic expressions. Then plot the sphere by using fsurf.

syms phi theta
r = 4;
x = r*sin(phi)*cos(theta);
y = r*sin(phi)*sin(theta);
z = r*cos(phi);
fsurf(x,y,z,[0 pi 0 2*pi])
axis equal

Figure contains an axes object. The axes object contains an object of type parameterizedfunctionsurface.

Plot a Half Sphere

Plot a half sphere with radius $r = 4$ .

In spherical coordinates, the sphere is parameterized by $(4, θ, ϕ)$ , with $ϕ$ ranging from $0$ to $π / 2$ and $θ$ ranging from $0$ to $2 π$ . Transform spherical coordinates to Cartesian coordinates by specifying the surface parameterization as symbolic expressions. Then plot the half sphere by using fsurf.

syms phi theta
r = 4;
x = r*sin(phi)*cos(theta);
y = r*sin(phi)*sin(theta);
z = r*cos(phi);
fsurf(x,y,z,[0 pi/2 0 2*pi])
axis equal

Figure contains an axes object. The axes object contains an object of type parameterizedfunctionsurface.

Plot a Parameterized Surface

Plot a parameterized surface whose radial distance in spherical coordinates is related to the azimuthal and polar angles.

The surface has radial coordinates $ρ = 2 + \sin (5 ϕ + 7 θ)$ , with $ϕ$ ranging from $0$ to $π$ and $θ$ ranging from $0$ to $2 π$ . Transform spherical coordinates to Cartesian coordinates by specifying the surface parameterization as symbolic expressions. Then plot the parameterized surface by using fsurf.

syms phi theta
rho = 2 + sin(5*phi + 7*theta);
x = rho*sin(phi)*cos(theta);
y = rho*sin(phi)*sin(theta);
z = rho*cos(phi);
fsurf(x,y,z,[0 pi 0 2*pi])
view(45,50)

Figure contains an axes object. The axes object contains an object of type parameterizedfunctionsurface.