本页采用了机器翻译。点击此处可查看英文原文。

可视化散点 ThingSpeak 数据的线性拟合

此示例使用:

打开脚本

此示例显示如何使用 Curve Fitting Toolbox&trade 直观显示环境温度和相对湿度之间的趋势。

从气象站 ThingSpeak 通道读取数据

ThingSpeak 通道 12397 包含来自位于马萨诸塞州纳蒂克的 MathWorks 气象站的数据。每分钟收集一次数据。字段 3 和 4 分别包含湿度和温度数据。使用 thingSpeakRead 函数从通道 12397 读取某一天的数据，例如 2016 年 5 月 1 日。

startDate = datetime('May 1, 2016 12:01 AM');
endDate = datetime('May 2, 2016 12:01 AM');
data = thingSpeakRead(12397,'DateRange',[startDate, endDate],'Fields',[3 4],'OutputFormat','Table');

用线性曲线拟合数据

暖空气比冷空气含有更多的水分。相对湿度是空气中的水分量与该温度下空气所能容纳的水分量之比。因此，随着空气变暖，空气可容纳的水分量增加，而空气的相对湿度降低。这表明环境空气温度和相对湿度之间存在反比关系。您可以对数据拟合一条线性线，看看是否存在反线性趋势。

fitObject = fit(data.TemperatureF,data.Humidity,'poly1');

绘制拟合数据

绘制拟合数据以查看线性曲线拟合是否捕捉到环境温度和相对湿度之间的关系。

figure;
plot(fitObject,data.TemperatureF,data.Humidity,'o');

xlabel('Ambient Temperature [^{\circ}F]');
ylabel('Relative Humidity [%]');
title('Linear Relationship Between Ambient Temperature and Relative Humidity');

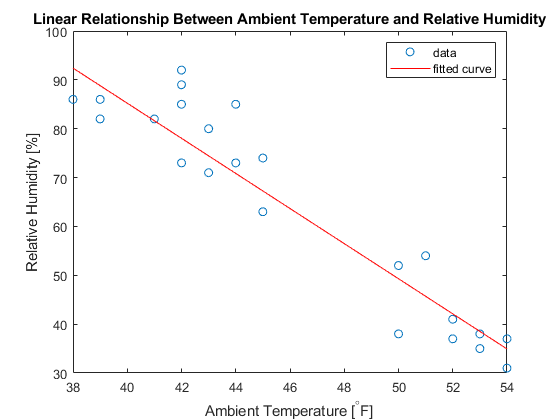
您可以看到拟合线具有负斜率，并且随着环境温度的升高，相对湿度降低，表明存在反线性关系。

另请参阅

函数