f = 
     Linear model Poly2:
     f(x) = p1*x^2 + p2*x + p3
     Coefficients (with 95% confidence bounds):
       p1 =    0.006541  (0.006124, 0.006958)
       p2 =      -23.51  (-25.09, -21.93)
       p3 =   2.113e+04  (1.964e+04, 2.262e+04)

f 包含拟合结果，包括 95% 置信边界的系数估计值。

绘制 f 中拟合的图以及数据散点图。

plot(f,cdate,pop)

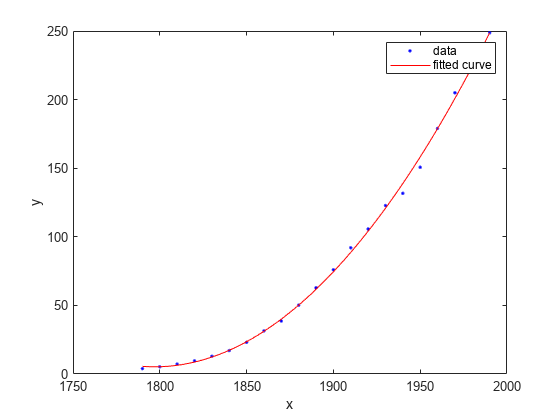
Figure contains an axes object. The axes object with xlabel x, ylabel y contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent Data, Fitted curve.

绘图显示，拟合曲线与人口数据高度吻合。

拟合多项式曲面

打开实时脚本

加载 franke 样本数据集。

load franke

向量 x、y 和 z 包含从弗兰克的二元测试函数生成的数据，并添加了噪声和缩放。

对数据进行多项式曲面拟合。为 x 项指定 2 次，为 y 项指定 3 次。

sf = fit([x, y],z,'poly23')

sf = 
     Linear model Poly23:
     sf(x,y) = p00 + p10*x + p01*y + p20*x^2 + p11*x*y + p02*y^2 + p21*x^2*y 
                    + p12*x*y^2 + p03*y^3
     Coefficients (with 95% confidence bounds):
       p00 =       1.118  (0.9149, 1.321)
       p10 =  -0.0002941  (-0.000502, -8.623e-05)
       p01 =       1.533  (0.7032, 2.364)
       p20 =  -1.966e-08  (-7.084e-08, 3.152e-08)
       p11 =   0.0003427  (-0.0001009, 0.0007863)
       p02 =      -6.951  (-8.421, -5.481)
       p21 =   9.563e-08  (6.276e-09, 1.85e-07)
       p12 =  -0.0004401  (-0.0007082, -0.0001721)
       p03 =       4.999  (4.082, 5.917)

sf 包含拟合结果，包括 95% 置信边界的系数估计值。

绘制 sf 中的拟合图以及数据散点图。

plot(sf,[x,y],z)

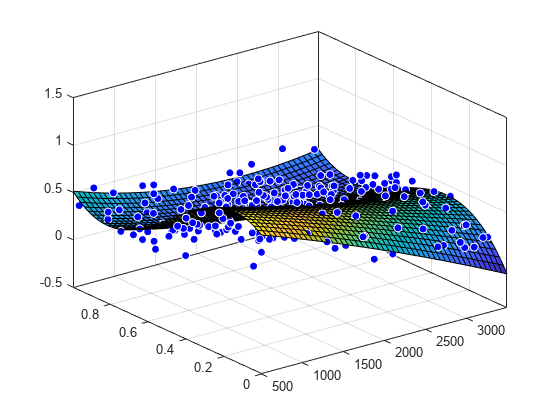
Figure contains an axes object. The axes object contains 2 objects of type line, surface. One or more of the lines displays its values using only markers

在拟合前创建拟合选项和拟合类型

打开实时脚本

加载并绘制数据图，使用 fittype 和 fitoptions 函数创建拟合选项和拟合类型，然后创建并绘制拟合图。

加载 census.mat 中的数据并绘制数据图。

load census
plot(cdate,pop,'o')

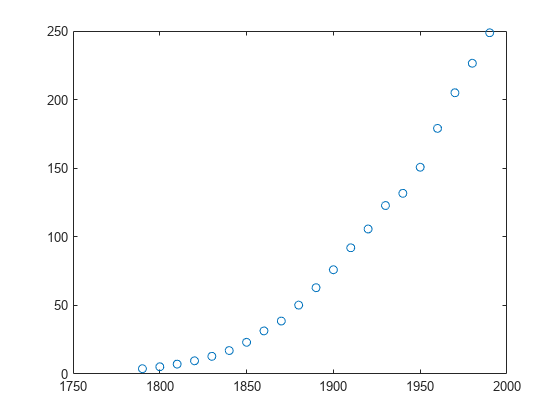
Figure contains an axes object. The axes contains a line object which displays its values using only markers.

为自定义非线性模型 $y = a (x - b)^{n}$ 创建一个拟合选项对象和一个拟合类型，其中 a 和 b 是系数，n 是问题相关参数。

fo = fitoptions('Method','NonlinearLeastSquares',...
               'Lower',[0,0],...
               'Upper',[Inf,max(cdate)],...
               'StartPoint',[1 1]);
ft = fittype('a*(x-b)^n','problem','n','options',fo);

使用拟合选项和值 n = 2 来拟合数据。

[curve2,gof2] = fit(cdate,pop,ft,'problem',2)

curve2 = 
     General model:
     curve2(x) = a*(x-b)^n
     Coefficients (with 95% confidence bounds):
       a =    0.006092  (0.005743, 0.006441)
       b =        1789  (1784, 1793)
     Problem parameters:
       n =           2

gof2 = struct with fields:
           sse: 246.1543
       rsquare: 0.9980
           dfe: 19
    adjrsquare: 0.9979
          rmse: 3.5994

使用拟合选项和值 n = 3 来拟合数据。

[curve3,gof3] = fit(cdate,pop,ft,'problem',3)

curve3 = 
     General model:
     curve3(x) = a*(x-b)^n
     Coefficients (with 95% confidence bounds):
       a =   1.359e-05  (1.245e-05, 1.474e-05)
       b =        1725  (1718, 1731)
     Problem parameters:
       n =           3

gof3 = struct with fields:
           sse: 232.0058
       rsquare: 0.9981
           dfe: 19
    adjrsquare: 0.9980
          rmse: 3.4944

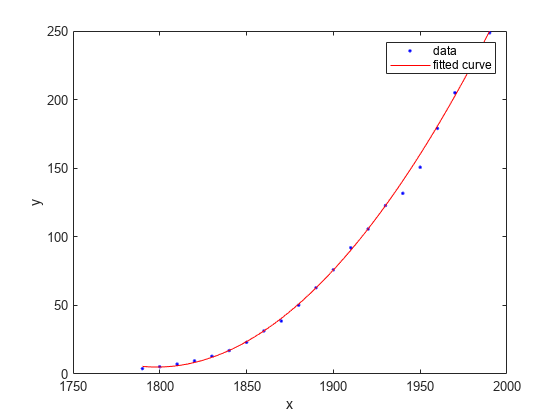
用数据绘制拟合结果图。

hold on
plot(curve2,'m')
plot(curve3,'c')
legend('Data','n=2','n=3')
hold off

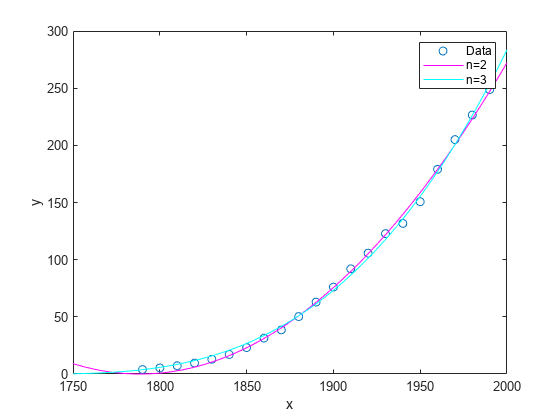
Figure contains an axes object. The axes object with xlabel x, ylabel y contains 3 objects of type line. One or more of the lines displays its values using only markers These objects represent Data, n=2, n=3.

拟合多个多项式

打开实时脚本

加载 carbon12alpha 核反应采样数据集。

load carbon12alpha

angle 是以弧度为单位的发射角度组成的向量。counts 是对应于 angle 中角度的原始 alpha 粒子计数组成的向量。

显示计数对角度的散点图。

scatter(angle,counts)

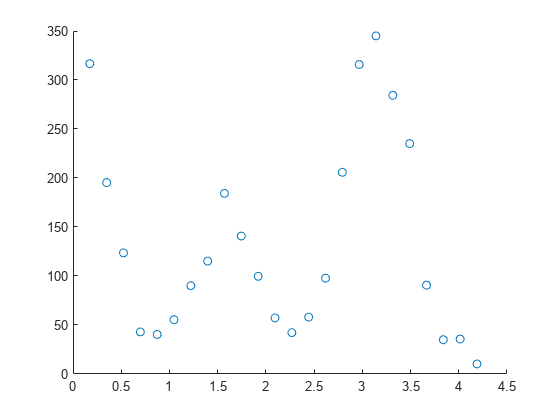
Figure contains an axes object. The axes object contains an object of type scatter.

散点图显示，计数会随着角度在 0 和 4.5 之间增大而发生振荡。要对数据进行多项式模型拟合，请将 fitType 输入参量指定为 "poly#"，其中 # 是 1 到 9 之间的整数。您可以拟合高达九次的模型。有关详细信息，请参阅曲线和曲面拟合的库模型列表。

对核反应数据进行五次、七次和九次多项式拟合。返回每个拟合的拟合优度统计量。

[f5,gof5] = fit(angle,counts,"poly5");
[f7,gof7] = fit(angle,counts,"poly7");
[f9,gof9] = fit(angle,counts,"poly9");

使用 linspace 函数生成一个由 0 和 4.5 之间的查询点组成的向量。计算查询点处的多项式拟合值，然后将它们与核反应数据一起绘图。

xq = linspace(0,4.5,1000);

figure
hold on
scatter(angle,counts,"k")
plot(xq,f5(xq))
plot(xq,f7(xq))
plot(xq,f9(xq))
ylim([-100,550])
legend("original data","fifth-degree polynomial","seventh-degree polynomial","ninth-degree polynomial")

Figure contains an axes object. The axes object contains 4 objects of type scatter, line. These objects represent original data, fifth-degree polynomial, seventh-degree polynomial, ninth-degree polynomial.

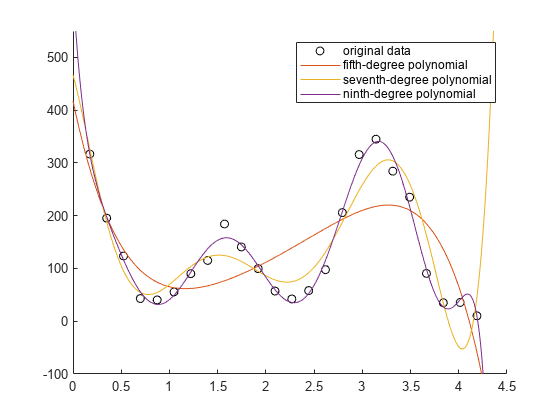
该绘图表明九次多项式最准确地描述了数据的情况。

使用 struct2table 函数显示每个拟合的拟合优度统计量。

gof = struct2table([gof5 gof7 gof9],RowNames=["f5" "f7" "f9"])

gof=3×5 table
             sse        rsquare    dfe    adjrsquare     rmse 
          __________    _______    ___    __________    ______

    f5    1.0901e+05    0.54614    18      0.42007       77.82
    f7         32695    0.86387    16      0.80431      45.204
    f9        3660.2    0.98476    14      0.97496      16.169

九次多项式拟合的误差平方和 (SSE) 小于五次和七次多项式拟合的 SSE。此结果证实九次多项式最准确地描述了数据的情况。

指定归一化和稳健选项

打开实时脚本

加载 census 样本数据集。进行三次多项式拟合，并指定 Normalize（中心化并缩放）和 Robust 拟合选项。

load census;
f = fit(cdate,pop,'poly3','Normalize','on','Robust','Bisquare')

f = 
     Linear model Poly3:
     f(x) = p1*x^3 + p2*x^2 + p3*x + p4
       where x is normalized by mean 1890 and std 62.05
     Coefficients (with 95% confidence bounds):
       p1 =     -0.4619  (-1.895, 0.9707)
       p2 =       25.01  (23.79, 26.22)
       p3 =       77.03  (74.37, 79.7)
       p4 =       62.81  (61.26, 64.37)

绘制拟合图。

plot(f,cdate,pop)

使用约束点拟合曲线

此示例使用:

打开实时脚本

生成具有指数趋势的数据，然后使用单项指数对数据进行拟合。绘制拟合图和数据图。

rng(2,"twister");
x = (0:0.2:10)';
y = 2*exp(0.2*x) + 0.2*randn(size(x));

% Without constraints
fitresult1 = fit(x,y,"exp1");
plot(fitresult1,x,y);
hold on

以第二个数据点作为约束，拟合一条新的指数曲线。由于这是一种非线性拟合类型，Algorithm 必须指定为 "Interior-Point"，才能使用约束点进行拟合。如果未指定，软件会在内部切换到使用 "Interior-Point" 算法。

% With constraints
point = [x(2) y(2)];
fitresult2 = fit(x,y,"exp1",ConstraintPoints=point,Algorithm="Interior-Point");
plot(fitresult2);
plot(point(:,1),point(:,2),"*");
legend("Data","Without Constraints","With Constraints", ...
    "Constraint Point",Location="best");

Figure contains an axes object. The axes object with xlabel x, ylabel y contains 4 objects of type line. One or more of the lines displays its values using only markers These objects represent Data, Without Constraints, With Constraints, Constraint Point.

拟合由文件定义的曲线

打开实时脚本

在文件中定义一个函数，并使用它来创建拟合类型和进行曲线拟合。

在 MATLAB ® 文件中定义一个函数。

type piecewiseLine.m

function y = piecewiseLine(x,a,b,c,k)
% PIECEWISELINE   A line made of two pieces

y = zeros(size(x));

% This example includes a for-loop and if statement
% purely for example purposes.
for i = 1:length(x)
    if x(i) < k
        y(i) = a + b.*x(i);
    else
        y(i) = a + b*k + c.*(x(i)-k); 
    end
end
end

保存该文件。

定义一些数据并创建一个指定函数 piecewiseLine 的拟合类型。

x = [0.81;0.91;0.13;0.91;0.63;0.098;0.28;0.55;...
    0.96;0.96;0.16;0.97;0.96];
y = [0.17;0.12;0.16;0.0035;0.37;0.082;0.34;0.56;...
    0.15;-0.046;0.17;-0.091;-0.071];
ft = fittype('piecewiseLine( x, a, b, c, k )')

ft = 
     General model:
     ft(a,b,c,k,x) = piecewiseLine( x, a, b, c, k )

ft 的输入是按字母顺序排列的系数，后跟自变量。请参阅匿名函数的输入顺序了解更多信息。

如果要控制系数的顺序，则可以使用匿名函数输入。例如，要更改系数 a 和 b 的顺序：

ft = fittype(@(b,a,c,k,x) piecewiseLine(x,a,b,c,k))

您必须最后指定自变量 x。

使用拟合类型 ft 创建拟合并绘制结果。

f = fit(x, y, ft, 'StartPoint', [1, 0, 1, 0.5]);
plot(f, x, y)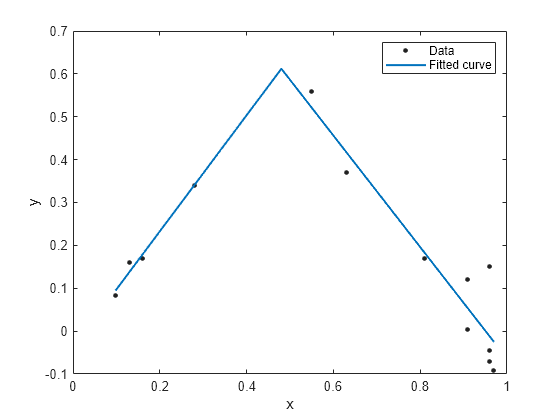

排除点并绘制显示排除数据的拟合图

打开实时脚本

在将排除的点作为拟合函数的输入提供之前，可以将这些点定义为变量。以下步骤重新创建前面示例中的拟合，并允许您对排除的点以及数据和拟合进行绘图。

加载数据并定义一个自定义方程和一些起点。

[x, y] = titanium;

gaussEqn = 'a*exp(-((x-b)/c)^2)+d'

gaussEqn = 
'a*exp(-((x-b)/c)^2)+d'

startPoints = [1.5 900 10 0.6]

startPoints = 1×4

    1.5000  900.0000   10.0000    0.6000

使用索引向量和表达式定义两组要排除的点。

exclude1 = [1 10 25];
exclude2 = x < 800;

使用自定义方程、起点和两个不同的排除点创建两个拟合。

f1 = fit(x',y',gaussEqn,'Start', startPoints, 'Exclude', exclude1);
f2 = fit(x',y',gaussEqn,'Start', startPoints, 'Exclude', exclude2);

对两个拟合绘图并突出显示排除的数据。

plot(f1,x,y,exclude1)
title('Fit with data points 1, 10, and 25 excluded')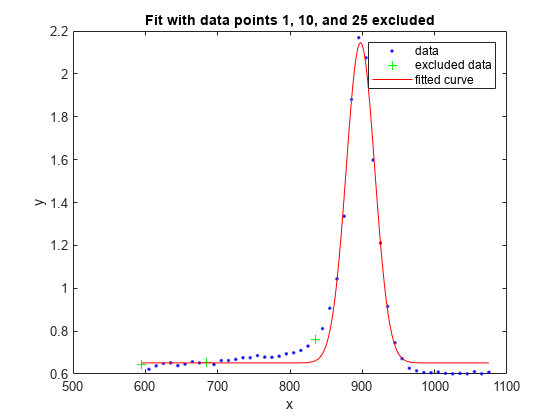

Figure contains an axes object. The axes object with title Fit with data points 1, 10, and 25 excluded, xlabel x, ylabel y contains 3 objects of type line. One or more of the lines displays its values using only markers These objects represent Data, Excluded data, Fitted curve.

figure; 
plot(f2,x,y,exclude2)
title('Fit with data points excluded such that x < 800')

Figure contains an axes object. The axes object with title Fit with data points excluded such that x < 800, xlabel x, ylabel y contains 3 objects of type line. One or more of the lines displays its values using only markers These objects represent Data, Excluded data, Fitted curve.

要创建一个具有排除点的曲面拟合示例，可加载某曲面数据，然后通过指定排除的数据来创建并绘制拟合。

load franke
f1 = fit([x y],z,'poly23', 'Exclude', [1 10 25]);
f2 = fit([x y],z,'poly23', 'Exclude', z > 1);

figure
plot(f1, [x y], z, 'Exclude', [1 10 25]);
title('Fit with data points 1, 10, and 25 excluded')

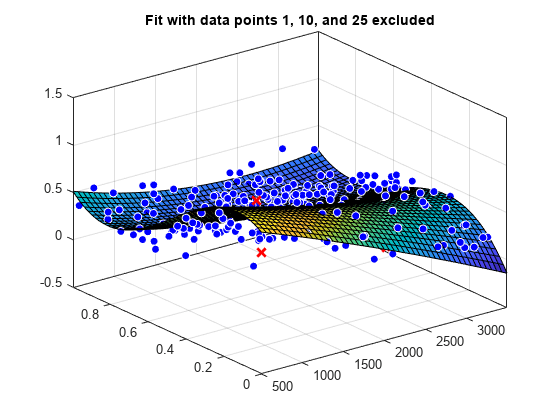
Figure contains an axes object. The axes object with title Fit with data points 1, 10, and 25 excluded contains 3 objects of type line, surface. One or more of the lines displays its values using only markers

figure
plot(f2, [x y], z, 'Exclude', z > 1);
title('Fit with data points excluded such that z > 1')

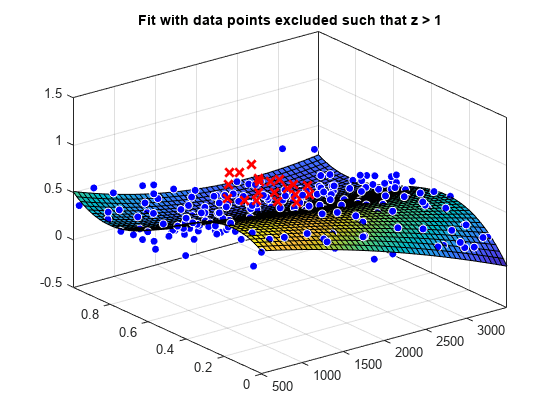
Figure contains an axes object. The axes object with title Fit with data points excluded such that z > 1 contains 3 objects of type line, surface. One or more of the lines displays its values using only markers

比较外插方法

打开实时脚本

使用 membrane 和 randn 函数生成一些含噪数据。

n = 41;
M = membrane(1,20)+0.02*randn(n);
[X,Y] = meshgrid(1:n);

矩阵 M 包含添加了噪声的 L 形膜的数据。矩阵 X 和 Y 分别包含 M 中对应元素的行和列索引值。

显示数据的曲面图。

figure(1)
surf(X,Y,M)

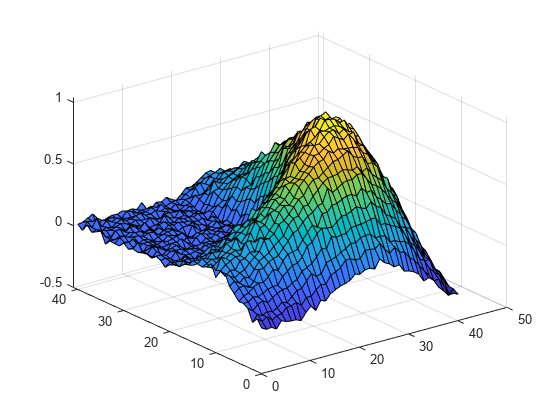
Figure contains an axes object. The axes object contains an object of type surface.

该图显示一个带褶皱的 L 形膜。膜上的褶皱是由数据中的噪声引起的。

使用线性插值通过带褶皱的膜对两个曲面进行拟合。对于第一个曲面，指定线性外插方法。对于第二个曲面，将外插方法指定为最近邻点。

flinextrap = fit([X(:),Y(:)],M(:),"linearinterp",ExtrapolationMethod="linear");
fnearextrap = fit([X(:),Y(:)],M(:),"linearinterp",ExtrapolationMethod="nearest");

通过使用 meshgrid 函数计算从 X 和 Y 数据的凸包延伸出去的查询点处的拟合值，以调查这些外插方法的不同之处。

[Xq,Yq] = meshgrid(-10:50);

Zlin = flinextrap(Xq,Yq);
Znear = fnearextrap(Xq,Yq);

绘制计算的拟合值图。

figure(2)
surf(Xq,Yq,Zlin)
title("Linear Extrapolation")
xlabel("X")
ylabel("Y")
zlabel("M")

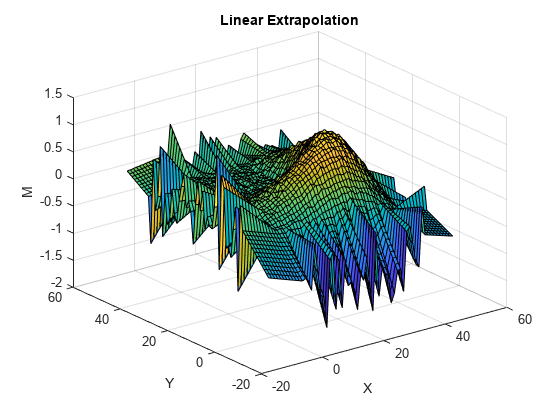
Figure contains an axes object. The axes object with title Linear Extrapolation, xlabel X, ylabel Y contains an object of type surface.

figure(3)
surf(Xq,Yq,Znear)
title("Nearest Neighbor Extrapolation")
xlabel("X")
ylabel("Y")
zlabel("M")

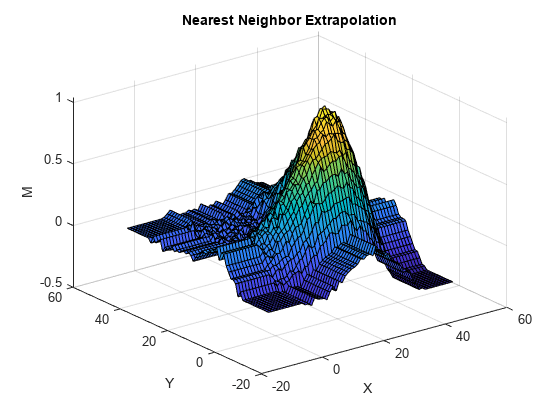
Figure contains an axes object. The axes object with title Nearest Neighbor Extrapolation, xlabel X, ylabel Y contains an object of type surface.

线性外插方法会在凸包外部生成尖峰。形成尖峰的平面区段沿着凸包边界上的点的梯度生成。最近邻点外插方法使用边界上的数据向各个方向延伸曲面。这种外插方法会生成模拟边界的波。

返回拟合优度统计量和拟合算法信息

打开实时脚本

进行平滑样条曲线拟合，并返回拟合优度统计量和有关拟合算法的信息。

加载 enso 样本数据集。enso 样本数据集包含复活节岛和澳大利亚达尔文之间的月平均大气压力差的数据。

load enso;

对 month 和 pressure 中的数据进行平滑样条曲线拟合，并返回拟合优度统计量和 output 结构体。

[curve,gof,output] = fit(month,pressure,"smoothingspline");

绘制拟合曲线图以及用于拟合该曲线的数据。

plot(curve,month,pressure);
xlabel("Month");
ylabel("Pressure");

Figure contains an axes object. The axes object with xlabel Month, ylabel Pressure contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent Data, Fitted curve.

绘制残差对 x 数据 (month) 的图。

plot(curve,month,pressure,"residuals")
xlabel("Month")
ylabel("Residuals")

Figure contains an axes object. The axes object with xlabel Month, ylabel Residuals contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent Data, Zero line.

使用 output 结构体中的 residuals 数据绘制残差对 y 数据 (pressure) 的图。要访问 output 的 residuals 字段，请使用圆点表示法。

residuals = output.residuals;
plot( pressure,residuals,".")
xlabel("Pressure")
ylabel("Residuals")

Figure contains an axes object. The axes object with xlabel Pressure, ylabel Residuals contains a line object which displays its values using only markers.

使用匿名函数拟合自定义模型

您可以使用匿名函数来更轻松地将其他数据传递到 fit 函数中。

在定义匿名函数之前，加载数据并将 Emax 设置为 1：

data = importdata( 'OpioidHypnoticSynergy.txt' );
Propofol      = data.data(:,1);
Remifentanil  = data.data(:,2);
Algometry     = data.data(:,3);
Emax = 1;

将模型方程定义为匿名函数：

Effect = @(IC50A, IC50B, alpha, n, x, y) ...
    Emax*( x/IC50A + y/IC50B + alpha*( x/IC50A )...
    .* ( y/IC50B ) ).^n ./(( x/IC50A + y/IC50B + ...
    alpha*( x/IC50A ) .* ( y/IC50B ) ).^n  + 1);

使用匿名函数 Effect 作为 fit 函数的输入，并绘制结果：

AlgometryEffect = fit( [Propofol, Remifentanil], Algometry, Effect, ...
    'StartPoint', [2, 10, 1, 0.8], ...
    'Lower', [-Inf, -Inf, -5, -Inf], ...
    'Robust', 'LAR' )
plot( AlgometryEffect, [Propofol, Remifentanil], Algometry )

有关使用匿名函数和其他自定义模型进行拟合的更多示例，请参阅 fittype 函数。

获取系数的顺序以便设置起点和边界

打开实时脚本

对于属性 Upper、Lower 和 StartPoint，您需要找到系数项的顺序。

创建一个拟合类型。

ft = fittype('b*x^2+c*x+a');

使用 coeffnames 函数获取系数的名称和顺序。

coeffnames(ft)

ans = 3×1 cell
    {'a'}
    {'b'}
    {'c'}

请注意，这与使用 fittype 创建 ft 的表达式中系数的顺序不同。

加载数据，创建一个拟合并设置起点。

load enso
fit(month,pressure,ft,'StartPoint',[1,3,5])

ans = 
     General model:
     ans(x) = b*x^2+c*x+a
     Coefficients (with 95% confidence bounds):
       a =       10.94  (9.362, 12.52)
       b =   0.0001677  (-7.985e-05, 0.0004153)
       c =     -0.0224  (-0.06559, 0.02079)

这会将初始值赋给系数，如下所示：a = 1，b = 3，c = 5。

您也可以获取拟合选项并设置起点和下界，然后使用新选项重新拟合。

options = fitoptions(ft)

options = 
  nlsqoptions with properties:

          StartPoint: []
           Algorithm: 'Trust-Region'
       DiffMinChange: 1.0000e-08
       DiffMaxChange: 0.1000
             Display: 'Notify'
         MaxFunEvals: 600
             MaxIter: 400
              TolFun: 1.0000e-06
                TolX: 1.0000e-06
               Lower: []
               Upper: []
    ConstraintPoints: []
              TolCon: 1.0000e-06
              Robust: 'Off'
           Normalize: 'off'
             Exclude: []
             Weights: []
              Method: 'NonlinearLeastSquares'

options.StartPoint = [10 1 3];
options.Lower = [0 -Inf 0];
fit(month,pressure,ft,options)

ans = 
     General model:
     ans(x) = b*x^2+c*x+a
     Coefficients (with 95% confidence bounds):
       a =       10.23  (9.448, 11.01)
       b =   4.335e-05  (-1.82e-05, 0.0001049)
       c =   5.523e-12  (fixed at bound)

输入参数

全部折叠

`x` — 要拟合的数据
矩阵

要拟合的数据，指定为包含一列（曲线拟合）或两列（曲面拟合）的矩阵。您可以使用 tablename.varname 指定 MATLAB^® 表中的变量。不能包含 Inf 或 NaN。拟合中仅使用复数数据的实部。

示例: x

示例: [x,y]

数据类型: double

`y` — 要拟合的数据
向量

要拟合的数据，指定为列向量，其行数与 x 相同。您可以使用 tablename.varname 在 MATLAB 表中指定变量。不能包含 Inf 或 NaN。拟合中仅使用复数数据的实部。

如果您的数据不是列向量形式，请使用 prepareCurveData 或 prepareSurfaceData。

数据类型: double

`z` — 要拟合的数据
向量

如果您的数据不是列向量形式，请使用 prepareSurfaceData。例如，如果您有 3 个矩阵，或您的数据是网格向量形式，其中 length(X) = n, length(Y) = m 且 size(Z) = [m,n]。

数据类型: double

`fitType` — 要拟合的模型类型
字符向量 | 字符串标量 | 字符串数组 | 字符向量元胞数组 | 匿名函数 | `fittype`

要拟合的模型类型，指定为表示库模型名称或 MATLAB 表达式的字符向量或字符串标量、线性模型项的字符串数组或这些项的字符向量元胞数组、匿名函数或用 fittype 函数创建的 fittype。您可以将 fittype 的任何有效的第一个输入用作 fit 的输入。

有关库模型名称的列表，请参阅模型名称和方程。

要拟合自定义模型，请使用 MATLAB 表达式、线性模型项的元胞数组或匿名函数。您还可以使用 fittype 函数创建 fittype，然后将其用作 fitType 输入参量的值。有关示例，请参阅使用匿名函数拟合自定义模型。有关使用线性模型项的示例，请参阅 fittype 函数。

示例: "poly2"

`fitOptions` — 算法选项
`fitoptions`

使用 fitoptions 函数构造的算法选项。这是为拟合选项指定名称-值对组参量的替代方法。

名称-值参数

全部展开

将可选参量对组指定为 Name1=Value1,...,NameN=ValueN，其中 Name 是参量名称，Value 是对应的值。名称-值参量必须出现在其他参量之后，但对各个参量对组的顺序没有要求。

在 R2021a 之前，使用逗号分隔每个名称和值，并用引号将 Name 引起来。

示例: Lower=[0,0],Upper=[Inf,max(x)],StartPoint=[1 1] 指定拟合方法、边界和起点。

所有拟合方法的选项

全部展开

`Normalize` — 中心化和缩放数据的选项
`'off'` (默认) | `'on'`

用于中心化和缩放数据的选项，指定为由 'Normalize' 和 'on' 或 'off' 组成的以逗号分隔的对组。

数据类型: char

`Exclude` — 要从拟合中排除的点
表达式 | 索引向量 | 逻辑向量 | 空

要从拟合中排除的点，指定为由 'Exclude' 和以下项之一组成的以逗号分隔的对组：

描述逻辑向量的表达式，例如 x > 10。
对要排除的点进行索引的整数组成的向量，例如 [1 10 25]。
所有数据点的逻辑向量，其中 true 表示离群值，由 excludedata 创建。

有关示例，请参阅排除点并绘制显示排除数据的拟合图。

数据类型: logical | double

`Weights` — 拟合的权重
[ ] (默认) | 向量

拟合的权重，指定为以逗号分隔的对组，其中包含 'Weights' 和与响应数据 y（曲线）或 z（曲面）大小相同的向量。

数据类型: double

`problem` — 赋给问题相关常量的值
元胞数组 | 双精度值

要赋给问题相关常量的值，指定为由 'problem' 和一个元胞数组组成的以逗号分隔的对组，该元胞数组中每个元素对应于一个与问题相关的常量。有关详细信息，请参阅 fittype。

数据类型: cell | double

平滑选项

全部展开

`SmoothingParam` — 平滑参数
范围 (0,1) 中的标量值

平滑参数，指定为以逗号分隔的对组，其中包含 'SmoothingParam' 和介于 0 和 1 之间的标量值。默认值取决于数据集。仅当拟合类型为 smoothingspline 时才可用。

数据类型: double

`Span` — 用于局部回归的数据点的比例
0.25 (默认) | 范围 (0,1) 中的标量值

用于局部回归的数据点的比例，指定为以逗号分隔的对组，其中包含 'Span' 和介于 0 和 1 之间的标量值。仅当拟合类型为 lowess 或 loess 时才可用。

数据类型: double

插值选项

全部展开

`ExtrapolationMethod` — 外插方法
`"auto"` (默认) | `"none"` | `"linear"` | `"nearest"` | `"thinplate"` | `"biharmonic"` | `"pchip"` | `"cubic"`

插值拟合的外插方法，指定为以下值之一。

值	描述	支持的拟合
`"auto"`	所有插值拟合类型的默认值。将 `ExtrapolationMethod` 设置为 `"auto"` 以便在拟合过程中自动指定外插方法。	所有插值拟合类型和 `cubicspline` 曲线拟合
`"none"`	无外插。拟合数据凸包外部的查询点的计算结果为 `NaN`。当您为 `cubicinterp` 和 `linearinterp` 曲面拟合将 `ExtrapolationMethod` 设置为 `"auto"` 时，`fit` 将外插方法设置为 `"none"`。	曲线拟合 - `cubicspline` 和 `pchipinterp` 曲面拟合 - `naturalinterp` 曲线拟合和曲面拟合 - `cubicinterp`、`linearinterp` 和 `nearestinterp`
`"linear"`	基于边界梯度的线性外插。当您为 `"linearinterp"` 曲线拟合将 `ExtrapolationMethod` 设置为 `"auto"` 时，`fit` 将外插方法设置为 `"linear"`。	曲面拟合 - `cubicinterp`、`nearestinterp` 和 `naturalinterp` 曲线拟合和曲面拟合 - `linearinterp`
`"nearest"`	最近邻点外插。这种方法的计算结果为拟合数据凸包边界上最近点的值。当您为 `"nearestinterp"` 曲线拟合和曲面拟合将 `ExtrapolationMethod` 设置为 `"auto"` 时，`fit` 将外插方法设置为 `"nearest"`。	曲线拟合 - `cubicspline` 和 `pchipinterp` 曲面拟合 - `naturalinterp` 曲线拟合和曲面拟合 - `cubicinterp`、`linearinterp` 和 `nearestinterp`
`"thinplate"`	薄板样条外插。这种方法可将薄板内插样条扩展到拟合数据的凸包之外。有关详细信息，请参阅 `tpaps`。当您为 `"thinplateinterp"` 曲面拟合将 `ExtrapolationMethod` 设置为 `"auto"` 时，`fit` 将外插方法设置为 `"thinplate"`。	曲面拟合 - `thinplateinterp`
`"biharmonic"`	双调和样条外插。这种方法可将双调和内插样条扩展到拟合数据的凸包之外。当您为 `"biharmonicinterp"` 曲面拟合将 `ExtrapolationMethod` 设置为 `"auto"` 时，`fit` 将外插方法设置为 `"biharmonic"`。	曲面拟合 - `biharmonicinterp`
`"pchip"`	分段三次埃尔米特插值多项式 (PCHIP) 外插。这种方法可将保形 PCHIP 扩展到拟合数据的凸包之外。有关详细信息，请参阅 `pchip`。当您为 `pchipinterp` 曲线拟合将 `ExtrapolationMethod` 设置为 `"auto"` 时，`fit` 将外插方法设置为 `"pchip"`。	曲线拟合 - `pchipinterp`
`"cubic"`	三次样条外插。这种方法可将三次插值样条扩展到拟合数据的凸包之外。当您为 `cubicinterp` 和 `cubicspline` 曲线拟合将 `ExtrapolationMethod` 设置为 `"auto"` 时，`fit` 将外插方法设置为 `"cubic"`。有关详细信息，请参阅 `spline`。	曲线拟合 - `cubicinterp` 和 `cubicspline`

数据类型: char | string

线性和非线性最小二乘选项

全部展开

`Robust` — 稳健线性最小二乘拟合方法
`'off'` (默认) | `LAR` | `Bisquare`

稳健线性最小二乘拟合方法，指定为以逗号分隔的对组，其中包含 'Robust' 和以下值之一：

'LAR' 指定最小绝对残差方法。
'Bisquare' 指定 bisquare 权重方法。

当拟合类型 Method 为 LinearLeastSquares 或 NonlinearLeastSquares 时可用。

数据类型: char

`Lower` — 要拟合的系数的下界
[ ] (默认) | 向量

要拟合的系数的下界，指定为以逗号分隔的对组，其中包含 'Lower' 和向量。默认值为一个空向量，表示拟合不受下界的约束。如果指定边界，则向量长度必须等于系数数目。使用 coeffnames 函数找出向量值中系数项的顺序。有关示例，请参阅获取系数的顺序以便设置起点和边界。各个无约束下界可以由 -Inf 指定。

当 Method 为 LinearLeastSquares 或 NonlinearLeastSquares 时可用。

数据类型: double

`Upper` — 要拟合的系数的上界
[ ] (默认) | 向量

要拟合的系数的上界，指定为以逗号分隔的对组，其中包含 'Upper' 和向量。默认值为一个空向量，表示拟合不受上界的约束。如果指定边界，则向量长度必须等于系数数目。使用 coeffnames 函数找出向量值中系数项的顺序。有关示例，请参阅获取系数的顺序以便设置起点和边界。各个无约束上界可以由 +Inf 指定。

当 Method 为 LinearLeastSquares 或 NonlinearLeastSquares 时可用。

数据类型: logical

`ConstraintPoints` — 拟合要经过的点
`[]` (默认) | 数值矩阵

自 R2025a 起

拟合要经过的点，指定为 nx2 数值矩阵（对于曲线），或 nx3 数值矩阵（对于曲面）。每行表示一个约束点，而每列表示该点的 x、y 或 z 坐标。约束点的数目不能大于指定 fitType 中系数的数目。您可以使用 numcoeffs 查找拟合类型中系数的数目。如果指定最大约束点数，则只能得到一个解，且该解与输入数据无关。

注意

您必须安装有 Optimization Toolbox™，才能使用约束点来拟合模型。

当 Method 为 LinearLeastSquares 或 NonlinearLeastSquares 时可用。

示例: [0 0; 1 5]

数据类型: double

`TolCon` — 约束点的容差
10^–6 (默认) | 非负数值标量

自 R2025a 起

约束点的容差，指定为非负数值标量。这是在发生违反约束之前，所提供约束点与拟合实际经过的点之间的绝对数值差异的上界。

如果 ConstraintPoints 名称-值参量未指定，则 TolCon 无效。

注意

TolCon 的运算原理不同于其他容差。即使满足 TolCon 条件，求解器仍继续运行，除非由于其他原因停止运行。求解器不会仅仅因为满足 TolCon 就停止。

当 Method 为 LinearLeastSquares 或 NonlinearLeastSquares 时可用。

数据类型: double

非线性最小二乘选项

全部展开

`StartPoint` — 系数的初始值
[ ] (默认) | 向量

系数的初始值，指定为以逗号分隔的对组，其中包含 'StartPoint' 和向量。使用 coeffnames 函数找出向量值中系数项的顺序。有关示例，请参阅获取系数的顺序以便设置起点和边界。

如果起点（空向量的默认值）未传递给 fit 函数，则某些库模型的起点是通过启发式方法确定的。对于有理和威布尔模型，以及所有自定义的非线性模型，工具箱从区间 (0,1) 中均匀随机地选择系数的默认初始值。因此，使用相同数据和模型的多个拟合可能导致不同的拟合系数。要避免这种情况，请使用 fitoptions 对象为系数指定初始值，或为 StartPoint 值指定向量值。