spline

三次样条数据插值

全页折叠

语法

s = spline(x,y,xq)

pp = spline(x,y)

说明

s = spline(x,y,xq) 返回与 xq 中的查询点对应的插值向量 s。s 的值由 x 和 y 的三次样条插值确定。

示例

pp = spline(x,y) 返回一个分段多项式结构体以用于 ppval 和样条实用工具 unmkpp。

示例

全部折叠

正弦数据的样条插值

打开实时脚本

使用 spline 基于非等间距的样本点对正弦曲线插值。

x = [0 1 2.5 3.6 5 7 8.1 10];
y = sin(x);
xx = 0:.25:10;
yy = spline(x,y,xx);
plot(x,y,'o',xx,yy)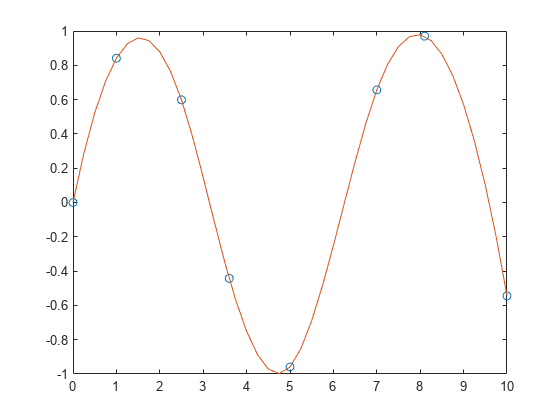

Figure contains an axes object. The axes object contains 2 objects of type line. One or more of the lines displays its values using only markers

具有指定端点斜率的样条插值

打开实时脚本

当端点斜率已知时，使用 clamped 或 complete 样条插值。为此，可以用两个额外元素指定值向量 $y$ （一个元素在起点，一个元素在终点）以定义端点斜率。

创建一个由数据 $y$ 组成的向量和另一个由数据的 $x$ 坐标组成的向量。

x = -4:4;
y = [0 .15 1.12 2.36 2.36 1.46 .49 .06 0];

使用 spline 进行数据插值并绘制结果。用两个额外值 [0 y 0] 指定第二个输入，以表示端点斜率均为零。使用 ppval 计算在插值区间中的 101 个点上的样条拟合。

cs = spline(x,[0 y 0]);
xx = linspace(-4,4,101);
plot(x,y,'o',xx,ppval(cs,xx),'-');

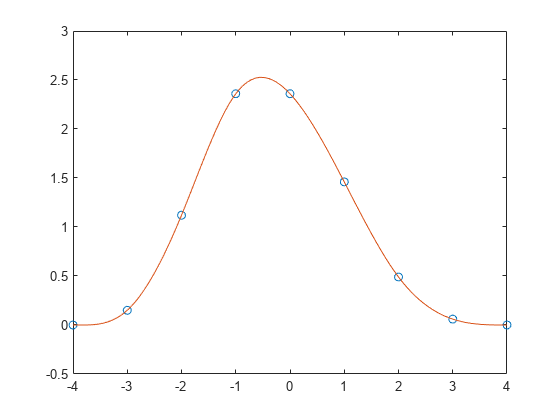
Figure contains an axes object. The axes object contains 2 objects of type line. One or more of the lines displays its values using only markers

使用三次样条外插

打开实时脚本

外插数据集以预测人口增长。

创建两个向量以表示从 1900 年至 1990 年的人口普查年 (t) 和相应的美国人口 (p)。

t = 1900:10:1990;
p = [ 75.995  91.972  105.711  123.203  131.669 ...
     150.697 179.323  203.212  226.505  249.633 ];

外插并使用三次样条预测 2000 年的人口。

spline(t,p,2000)

ans = 
270.6060

角数据的样条插值

打开实时脚本

使用带有标记 o 的五个数据点 y(:,2),...,y(:,6) 生成圆的绘图。矩阵 y 比 x 多两列。因此，spline 使用 y(:,1) 和 y(:,end) 作为端点斜率。圆在点 (1,0) 处开始和结束，因此该点被绘制两次。

x = pi*[0:.5:2]; 
y = [0  1  0 -1  0  1  0; 
     1  0  1  0 -1  0  1];
pp = spline(x,y);
yy = ppval(pp, linspace(0,2*pi,101));
plot(yy(1,:),yy(2,:),'-b',y(1,2:5),y(2,2:5),'or')
axis equal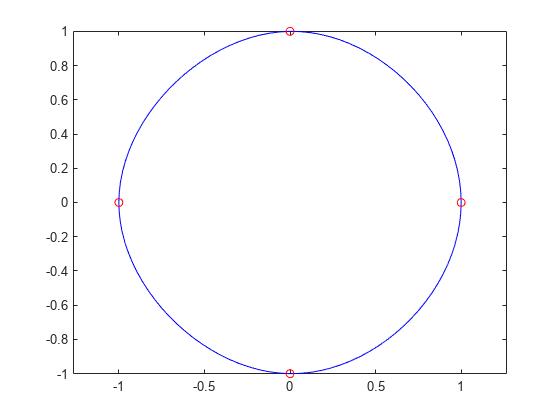

Figure contains an axes object. The axes object contains 2 objects of type line. One or more of the lines displays its values using only markers

正弦和余弦数据的样条插值

打开实时脚本

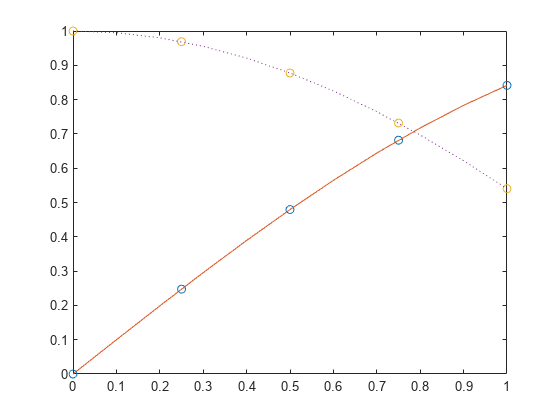
使用样条曲线在更精细的网格上对函数采样。

为几个值生成的正弦和余弦曲线介于 0 和 1 之间。使用样条插值在更精细的网格上对函数采样。

x = 0:.25:1;
Y = [sin(x); cos(x)];
xx = 0:.1:1;
YY = spline(x,Y,xx);
plot(x,Y(1,:),'o',xx,YY(1,:),'-')
hold on
plot(x,Y(2,:),'o',xx,YY(2,:),':')
hold off

Figure contains an axes object. The axes object contains 4 objects of type line. One or more of the lines displays its values using only markers

使用 `spline`、`pchip` 和 `makima` 的数据插值

打开实时脚本

将 spline、pchip 和 makima 为两个不同数据集生成的插值结果进行比较。这些函数都执行不同形式的分段三次 Hermite 插值。每个函数计算插值斜率的方式不同，因此它们在基础数据的平台区或波动处展现出不同行为。

对连接两个平台区的样本数据进行插值，并比较结果。创建由 x 值、点 y 处的函数值以及查询点 xq 组成的向量。使用 spline、pchip 和 makima 计算查询点处的插值。绘制查询点处的插值函数值以进行比较。

x = -3:3; 
y = [-1 -1 -1 0 1 1 1]; 
xq1 = -3:.01:3;
p = pchip(x,y,xq1);
s = spline(x,y,xq1);
m = makima(x,y,xq1);
plot(x,y,'o',xq1,p,'-',xq1,s,'-.',xq1,m,'--')
legend('Sample Points','pchip','spline','makima','Location','SouthEast')

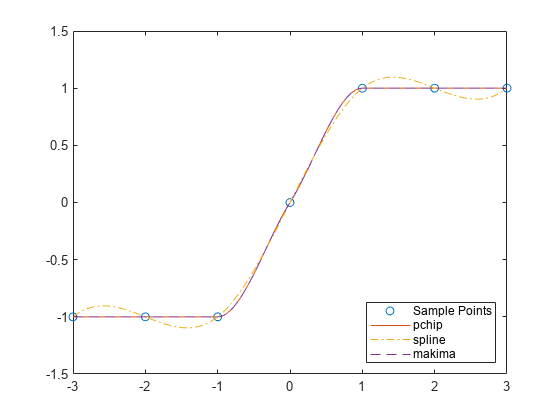
Figure contains an axes object. The axes object contains 4 objects of type line. One or more of the lines displays its values using only markers These objects represent Sample Points, pchip, spline, makima.

在本例中，pchip 和 makima 具有相似的行为，因为它们可以避免过冲，并且可以准确地连接平台区。

使用振动采样函数执行第二次比较。

x = 0:15;
y = besselj(1,x);
xq2 = 0:0.01:15;
p = pchip(x,y,xq2);
s = spline(x,y,xq2);
m = makima(x,y,xq2);
plot(x,y,'o',xq2,p,'-',xq2,s,'-.',xq2,m,'--')
legend('Sample Points','pchip','spline','makima')

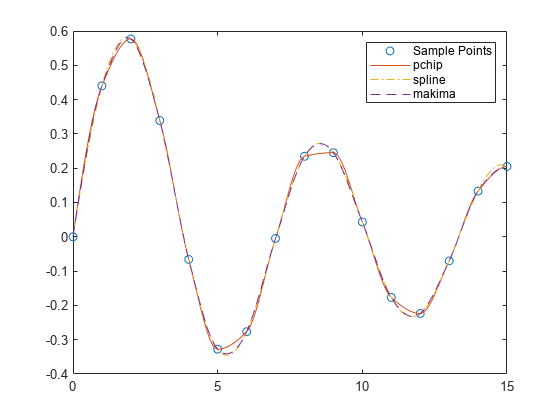
当底层函数振荡时，spline 和 makima 能够比 pchip 更好地捕获点之间的移动，后者会在局部极值附近急剧展平。

输入参数

全部折叠

`x` — x 坐标
向量

x 坐标，指定为向量。向量 x 指定提供数据 y 的点。x 的元素必须是唯一的。

三次样条插值需要至少 4 个点，如果分别提供了 2 个或 3 个点，则退回到线性或二次插值。

数据类型: single | double

`y` — x 坐标处的函数值
向量 | 矩阵 | 数组

在 x 坐标处的函数值，指定为数值向量、矩阵或数组。x 和 y 通常具有相同的长度，但 y 也可以比 x 正好多出两个元素，用以指定端点斜率。

如果 y 是矩阵或数组，则在获取最后一个维度 y(:,...,:,j) 中的值时应使其匹配 x。在此情况下，y 的最后一个维度的长度必须与 x 相同或正好多出两个元素。

三次样条的端点斜率遵循以下规则：

如果 x 和 y 是大小相等的向量，则使用非节点终止条件。
如果 x 或 y 为标量，则会将该标量扩展为与另一方具有相同的长度并使用非节点终止条件。
如果 y 是一个包含的值比 x 具有的条目多两个的向量，则 spline 使用 y 中的第一个和最后一个值作为三次样条的端点斜率。例如，如果 y 是一个向量，则：
- y(2:end-1) 给出 x 中每个点处的函数值
- y(1) 给出区间开始处 min(x) 的斜率
- y(end) 给出区间结束处 max(x) 的斜率
同样，如果 y 是一个矩阵或 size(y,N) 等于 length(x)+2 的 N 维数组，则：
- y(:,...,:,j+1) 给出 x 中每个点的函数值，其中 j = 1:length(x)
- y(:,:,...:,1) 给出区间开始处 min(x) 的斜率
- y(:,:,...:,end) 给出区间结束处 max(x) 的斜率

数据类型: single | double

`xq` — 查询点
标量 | 向量 | 矩阵 | 数组

查询点，指定为标量、向量、矩阵或数组。xq 中指定的点是 spline 计算出的插值函数值 yq 的 x 坐标。

数据类型: single | double

输出参量

全部折叠

`s` — 查询点位置的插值
标量 | 向量 | 矩阵 | 数组

查询点处的插值，以标量、向量、矩阵或数组形式返回。

s 的大小与 y 和 xq 的大小相关：

如果 y 为向量，则 s 的大小与 xq 相同。
如果 y 是大小为 Ny = size(y) 的数组，则下列条件适用：
- 如果 xq 为标量或向量，则 size(s) 返回 [Ny(1:end-1) length(xq)]。
- 如果 xq 是数组，则 size(s) 返回 [Ny(1:end-1) size(xq)]。

`pp` — 分段多项式
结构体

分段多项式，以结构体形式返回。将此结构体与 ppval 函数结合使用可计算一个或多个查询点处的分段多项式。该结构体包含以下字段。

字段	描述
`form`	`'pp'`（分段多项式）
`breaks`	包含严格递增元素的长度为 `L+1` 的向量，这些元素代表 `L` 个区间中每个区间的开始点和结束点
`coefs`	`L`×`k` 矩阵，其中每行 `coefs(i,:)` 包含第 `i` 个区间 `[breaks(i),breaks(i+1)]` 上 `k` 次多项式的局部系数
`pieces`	段数 `L`
`order`	多项式的阶
`dim`	目标的维度

由于 coefs 中的多项式系数是每个区间的本地系数，因此您必须减去对应节点区间的较低端点，以使用传统多项式方程中的系数。换言之，对于区间 [x1,x2] 上的系数 [a,b,c,d]，对应的多项式为

$f (x) = a {(x - x_{1})}^{3} + b {(x - x_{1})}^{2} + c (x - x_{1}) + d .$

提示

也可以结合使用 interp1 函数与 interp1(x,y,xq,'spline') 命令来执行样条插值。spline 对输入矩阵的行执行插值，而 interp1 对输入矩阵的列执行插值。

算法

通过求解三对角线性系统（可能具有多个右侧），获取所需信息来描述构成插值样条的各种三次多项式的系数。spline 使用函数 ppval、mkpp 和 unmkpp。这些例程组成可与分段多项式一起使用的一小套函数。要获得更多高级功能，请参阅 interp1 或 Curve Fitting Toolbox™ 样条函数。

参考

[1] de Boor, Carl. A Practical Guide to Splines. Springer-Verlag, New York: 1978.

扩展功能

全部展开

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

用法说明和限制：

输入 x 必须严格递增。
代码生成不会删除具有 NaN 值的 y 条目。
代码生成不会对 y 中的无限端点斜率报告错误。
为 pp = spline(x,y) 语法生成代码时，不能为 MATLAB^® 中的 ppval 函数输入 pp。要从代码生成器创建的 pp 结构体中创建一个 MATLAB pp 结构体：
- 在代码生成中，使用 unmkpp 将分段多项式详细信息返回给 MATLAB。
- 在 MATLAB 中，使用 mkpp 创建 pp 结构体。
如果您提供 xq，并且 y 具有可变大小且不是可变长度向量，则生成的代码中向量输出的方向可能与 MATLAB 中的方向不匹配。

基于线程的环境
使用 MATLAB® `backgroundPool` 在后台运行代码或使用 Parallel Computing Toolbox™ `ThreadPool` 加快代码运行速度。

此函数完全支持基于线程的环境。有关详细信息，请参阅在基于线程的环境中运行 MATLAB 函数。

GPU 数组
通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。

spline 函数支持 GPU 数组输入，但有以下用法说明和限制：

输入参量 y 必须是非稀疏值。

有关详细信息，请参阅在 GPU 上运行 MATLAB 函数 (Parallel Computing Toolbox)。

版本历史记录

在 R2006a 之前推出

另请参阅

interp1 | pchip | makima | ppval

spline

语法

说明

示例

正弦数据的样条插值

具有指定端点斜率的样条插值

使用三次样条外插

角数据的样条插值

正弦和余弦数据的样条插值

使用 spline、pchip 和 makima 的数据插值

输入参数

x — x 坐标 向量

y — x 坐标处的函数值 向量 | 矩阵 | 数组

xq — 查询点 标量 | 向量 | 矩阵 | 数组

输出参量

s — 查询点位置的插值 标量 | 向量 | 矩阵 | 数组

pp — 分段多项式 结构体

提示

算法

参考

扩展功能

C/C++ 代码生成 使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

基于线程的环境 使用 MATLAB® backgroundPool 在后台运行代码或使用 Parallel Computing Toolbox™ ThreadPool 加快代码运行速度。

GPU 数组 通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。

版本历史记录

另请参阅

使用 `spline`、`pchip` 和 `makima` 的数据插值

`x` — x 坐标
向量

`y` — x 坐标处的函数值
向量 | 矩阵 | 数组

`xq` — 查询点
标量 | 向量 | 矩阵 | 数组

`s` — 查询点位置的插值
标量 | 向量 | 矩阵 | 数组

`pp` — 分段多项式
结构体

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

基于线程的环境
使用 MATLAB® `backgroundPool` 在后台运行代码或使用 Parallel Computing Toolbox™ `ThreadPool` 加快代码运行速度。

GPU 数组
通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。