makima

修正 Akima 分段三次 Hermite 插值

全页折叠

语法

yq = makima(x,y,xq)

pp = makima(x,y)

说明

yq = makima(x,y,xq) 使用采样点 x 处的值 y 执行修正 Akima 插值，以求出查询点 xq 处的插值 yq。

示例

pp = makima(x,y) 返回一个分段多项式结构体以用于 ppval 和样条实用工具 unmkpp。

示例

全部折叠

余弦数据的 Akima 插值

打开实时脚本

使用 makima 对非等间距采样点上的余弦曲线进行插值。

x = [0 1 2.5 3.6 5 7 8.1 10];
y = cos(x);
xq = 0:.25:10;
yq = makima(x,y,xq);
plot(x,y,'o',xq,yq,'--')

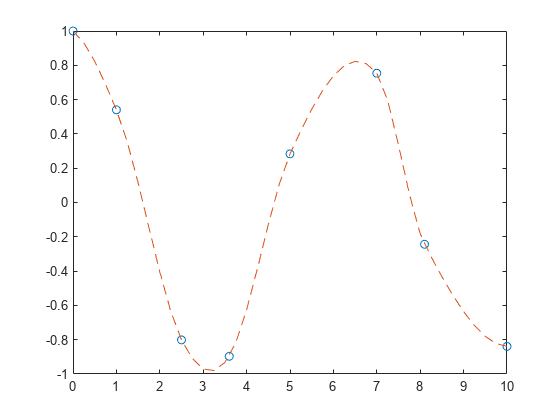
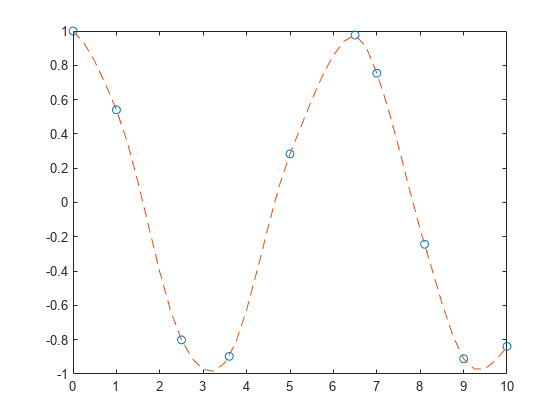
Figure contains an axes object. The axes object contains 2 objects of type line. One or more of the lines displays its values using only markers

Akima 算法利用振荡函数使局部极值附近的曲线展平。为了补偿这种展平，您可以在局部极值附近添加更多采样点。

在 $x = 6.5$ 和 $x = 9$ 附近添加采样点，然后重新绘制插值。

x = [0 1 2.5 3.6 5 6.5 7 8.1 9 10];
y = cos(x);
xq = 0:.25:10;
yq = makima(x,y,xq);
plot(x,y,'o',xq,yq,'--')

Figure contains an axes object. The axes object contains 2 objects of type line. One or more of the lines displays its values using only markers

使用 `spline`、`pchip` 和 `makima` 的数据插值

打开实时脚本

将 spline、pchip 和 makima 为两个不同数据集生成的插值结果进行比较。这些函数都执行不同形式的分段三次 Hermite 插值。每个函数计算插值斜率的方式不同，因此它们在基础数据的平台区或波动处展现出不同行为。

对连接两个平台区的样本数据进行插值，并比较结果。创建由 x 值、点 y 处的函数值以及查询点 xq 组成的向量。使用 spline、pchip 和 makima 计算查询点处的插值。绘制查询点处的插值函数值以进行比较。

x = -3:3; 
y = [-1 -1 -1 0 1 1 1]; 
xq1 = -3:.01:3;
p = pchip(x,y,xq1);
s = spline(x,y,xq1);
m = makima(x,y,xq1);
plot(x,y,'o',xq1,p,'-',xq1,s,'-.',xq1,m,'--')
legend('Sample Points','pchip','spline','makima','Location','SouthEast')

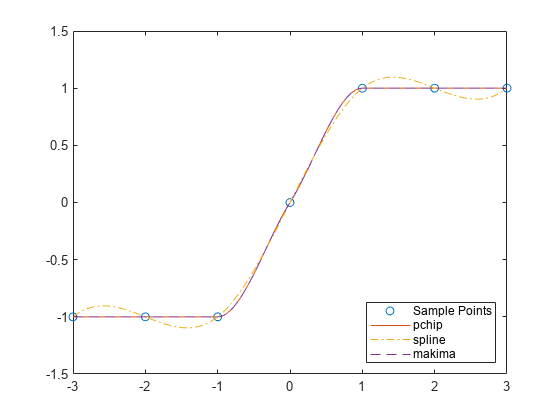
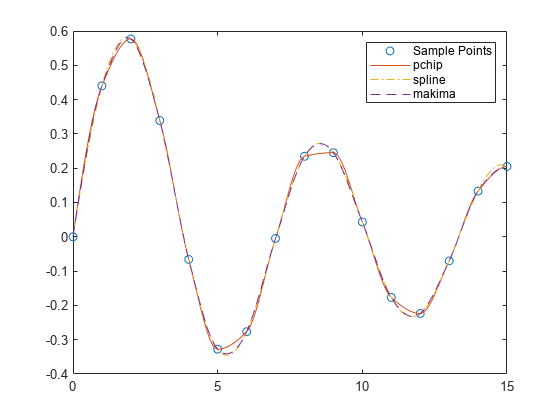
Figure contains an axes object. The axes object contains 4 objects of type line. One or more of the lines displays its values using only markers These objects represent Sample Points, pchip, spline, makima.

在本例中，pchip 和 makima 具有相似的行为，因为它们可以避免过冲，并且可以准确地连接平台区。

使用振动采样函数执行第二次比较。

x = 0:15;
y = besselj(1,x);
xq2 = 0:0.01:15;
p = pchip(x,y,xq2);
s = spline(x,y,xq2);
m = makima(x,y,xq2);
plot(x,y,'o',xq2,p,'-',xq2,s,'-.',xq2,m,'--')
legend('Sample Points','pchip','spline','makima')

当基础函数振荡时，spline 和 makima 能够比 pchip 更好地捕获点之间的移动，后者会在局部极值附近急剧展平。

使用分段多项式结构体进行 Akima 插值

打开实时脚本

创建采样点 x 及其值 y 的向量。使用 makima 为数据构造一个分段多项式结构体。

x = -5:5;
y = [1 1 1 0 0 1 1 2 2 2 2];
pp = makima(x,y)

pp = struct with fields:
      form: 'pp'
    breaks: [-5 -4 -3 -2 -1 0 1 2 3 4 5]
     coefs: [10×4 double]
    pieces: 10
     order: 4
       dim: 1

该结构体包含涵盖整个数据的 10 个 4 阶多项式的信息。pp.coefs(i,:) 包含在断点 [breaks(i) breaks(i+1)] 定义的区域内有效的多项式的系数。

结合 ppval 使用该结构体以计算几个查询点处的插值，然后绘制结果。在有三个或更多连续等值点的区域，Akima 算法用直线将这些点连接起来。

xq = -5:0.2:5;
m = ppval(pp,xq);
plot(x,y,'o',xq,m,'-.')
ylim([-0.2 2.2])

Figure contains an axes object. The axes object contains 2 objects of type line. One or more of the lines displays its values using only markers

输入参数

全部折叠

`x` — 样本点
向量

样本点，指定为一个向量。向量 x 指定提供数据 y 的点。x 的元素必须是唯一的。

数据类型: single | double

`y` — 样本点处的函数值
向量 | 矩阵 | 数组

样本点处的函数值，指定为数值向量、矩阵或数组。x 和 y 的长度必须相同。

如果 y 是矩阵或数组，则在获取最后一个维度 y(:,...,:,j) 中的值时应使其匹配 x。在此情况下，y 的最后一个维度的长度必须与 x 相同。

数据类型: single | double

`xq` — 查询点
标量 | 向量 | 矩阵 | 数组

查询点，指定为标量、向量、矩阵或数组。xq 中指定的点是 makima 计算出的插值函数值 yq 的 x 坐标。

数据类型: single | double

输出参量

全部折叠

`yq` — 查询点位置的插值
标量 | 向量 | 矩阵 | 数组

查询点处的插值，以标量、向量、矩阵或数组形式返回。yq 的大小与 y 和 xq 的大小相关：

如果 y 为向量，则 yq 的大小与 xq 相同。
如果 y 是大小为 Ny = size(y) 的数组，则下列条件适用：
- 如果 xq 为标量或向量，则 size(yq) 返回 [Ny(1:end-1) length(xq)]。
- 如果 xq 是数组，则 size(yq) 返回 [Ny(1:end-1) size(xq)]。

`pp` — 分段多项式
结构体

分段多项式，以结构体形式返回。将此结构体与 ppval 函数结合使用可计算一个或多个查询点处的插值多项式。该结构体包含以下字段。

字段	描述
`form`	`'pp'`（分段多项式）
`breaks`	包含严格递增元素的长度为 `L+1` 的向量，这些元素代表 `L` 个区间中每个区间的开始点和结束点
`coefs`	`L`×`k` 矩阵，其中每行 `coefs(i,:)` 包含第 `i` 个区间 `[breaks(i),breaks(i+1)]` 上 `k` 次多项式的局部系数
`pieces`	段数 `L`
`order`	多项式的阶
`dim`	目标的维度

由于 coefs 中的多项式系数是每个区间的本地系数，因此您必须减去对应节点区间的较低端点，以使用传统多项式方程中的系数。换言之，对于区间 [x1,x2] 上的系数 [a,b,c,d]，对应的多项式为

$f (x) = a {(x - x_{1})}^{3} + b {(x - x_{1})}^{2} + c (x - x_{1}) + d .$

详细信息

全部折叠

修正 Akima 插值

[1] 和 [2] 中所述的一维插值 Akima 算法执行三次插值以生成具有连续一阶导数 (C1) 的分段多项式。该算法可避免局部过度波动。

如果 $δ_{i} = \frac{v_{i + 1} - v_{i}}{x_{i + 1} - x_{i}}$ 是区间 $[x_{i} x_{i + 1})$ 上的斜率，则采样点 $x_{i}$ 处的导数 $d_{i}$ 的值是附近斜率的加权平均值：

$d_{i} = \frac{w_{1}}{w_{1} + w_{2}} δ_{i - 1} + \frac{w_{2}}{w_{1} + w_{2}} δ_{i} .$

在 Akima 的原始公式中，权重是：

$\begin{array}{l} w_{1} = | δ_{i + 1} - δ_{i} |, \\ w_{2} = | δ_{i - 1} - δ_{i - 2} | . \end{array}$

原始 Akima 算法对两侧的点赋予相等的权重，从而均匀地划分波动。

当两个具有不同斜率的平台区相遇时，对原始 Akima 算法所做的修改会对斜率更接近于零的一侧赋予更多权重。此修正优先考虑更接近水平的一侧，这样更直观并可避免过冲。特别是，每当有三个或更多连续共线点时，该算法将这些点用一条直线连接，从而避免过冲。

修正 Akima 算法中使用的权重为：

$\begin{array}{l} w_{1} = | δ_{i + 1} - δ_{i} | + \frac{| δ_{i + 1} + δ_{i} |}{2}, \\ w_{2} = | δ_{i - 1} - δ_{i - 2} | + \frac{| δ_{i - 1} + δ_{i - 2} |}{2} . \end{array}$

与 spline 算法相比，Akima 算法产生的波动较少，更适合处理平台区之间的快速变化。与 pchip 算法相比，Akima 算法不那么急剧展平，因此仍然能够处理振荡数据。

参考

[1] Akima, Hiroshi. "A new method of interpolation and smooth curve fitting based on local procedures." Journal of the ACM (JACM) , 17.4, 1970, pp. 589–602.

[2] Akima, Hiroshi. "A method of bivariate interpolation and smooth surface fitting based on local procedures." Communications of the ACM , 17.1, 1974, pp. 18–20.

扩展功能

全部展开

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

用法说明和限制：

输入 x 必须严格递增。
代码生成不会删除具有 NaN 值的 y 条目。
为 pp = makima(x,y) 语法生成代码时，不能为 MATLAB^® 中的 ppval 函数输入 pp。要从代码生成器创建的 pp 结构体中创建一个 MATLAB pp 结构体：
- 在代码生成中，使用 unmkpp 将分段多项式详细信息返回给 MATLAB。
- 在 MATLAB 中，使用 mkpp 创建 pp 结构体。
如果您提供 xq，并且 y 具有可变大小且不是可变长度向量，则生成的代码中向量输出的方向可能与 MATLAB 中的方向不匹配。

基于线程的环境
使用 MATLAB® `backgroundPool` 在后台运行代码或使用 Parallel Computing Toolbox™ `ThreadPool` 加快代码运行速度。

此函数完全支持基于线程的环境。有关详细信息，请参阅在基于线程的环境中运行 MATLAB 函数。

GPU 数组
通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。

makima 函数完全支持 GPU 数组。要在 GPU 上运行该函数，请将输入数据指定为 gpuArray (Parallel Computing Toolbox)。有关详细信息，请参阅在 GPU 上运行 MATLAB 函数 (Parallel Computing Toolbox)。

分布式数组
使用 Parallel Computing Toolbox™ 在集群的组合内存中对大型数组进行分区。

用法说明和限制：

分布式数组不支持 makima(x,y) 语法。

有关详细信息，请参阅使用分布式数组运行 MATLAB 函数 (Parallel Computing Toolbox)。

版本历史记录

在 R2019b 中推出

另请参阅

interp1 | spline | pchip | ppval

外部网站

Cleve's Corner:Makima Piecewise Cubic Interpolation

makima

语法

说明

示例

余弦数据的 Akima 插值

使用 spline、pchip 和 makima 的数据插值

使用分段多项式结构体进行 Akima 插值

输入参数

x — 样本点 向量

y — 样本点处的函数值 向量 | 矩阵 | 数组

xq — 查询点 标量 | 向量 | 矩阵 | 数组

输出参量

yq — 查询点位置的插值 标量 | 向量 | 矩阵 | 数组

pp — 分段多项式 结构体

详细信息

修正 Akima 插值

参考

扩展功能

C/C++ 代码生成 使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

基于线程的环境 使用 MATLAB® backgroundPool 在后台运行代码或使用 Parallel Computing Toolbox™ ThreadPool 加快代码运行速度。

GPU 数组 通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。

分布式数组 使用 Parallel Computing Toolbox™ 在集群的组合内存中对大型数组进行分区。

版本历史记录

另请参阅

外部网站

使用 `spline`、`pchip` 和 `makima` 的数据插值

`x` — 样本点
向量

`y` — 样本点处的函数值
向量 | 矩阵 | 数组

`xq` — 查询点
标量 | 向量 | 矩阵 | 数组

`yq` — 查询点位置的插值
标量 | 向量 | 矩阵 | 数组

`pp` — 分段多项式
结构体

C/C++ 代码生成
使用 MATLAB® Coder™ 生成 C 代码和 C++ 代码。

基于线程的环境
使用 MATLAB® `backgroundPool` 在后台运行代码或使用 Parallel Computing Toolbox™ `ThreadPool` 加快代码运行速度。

GPU 数组
通过使用 Parallel Computing Toolbox™ 在图形处理单元 (GPU) 上运行来加快代码执行。

分布式数组
使用 Parallel Computing Toolbox™ 在集群的组合内存中对大型数组进行分区。