ppval

计算分段多项式

全页折叠

语法

v = ppval(pp,xq)

说明

v = ppval(pp,xq) 在查询点 xq 处计算分段多项式 pp。

示例

示例

全部折叠

打开实时脚本

创建一个分段多项式，它在区间 [0,4] 内具有三次多项式，在区间 [4,10] 内具有二次多项式，在区间 [10,15] 内具有四次多项式。

breaks = [0 4 10 15];
coefs = [0 1 -1 1 1; 0 0 1 -2 53; -1 6 1 4 77];
pp = mkpp(breaks,coefs)
pp = struct with fields:
      form: 'pp'
    breaks: [0 4 10 15]
     coefs: [3×5 double]
    pieces: 3
     order: 5
       dim: 1

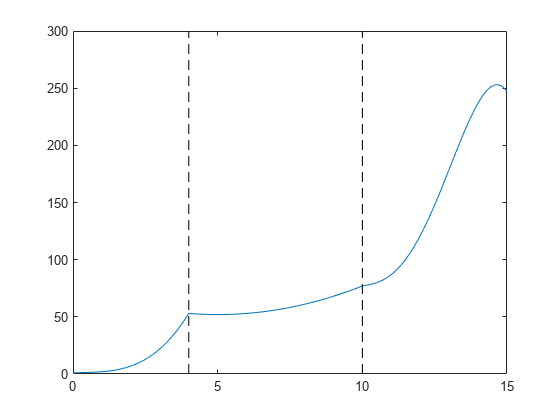
计算区间 [0,15] 内多个点处的分段多项式，并绘制结果图。在多项式汇合的断点处绘制垂直虚线。

xq = 0:0.01:15;
plot(xq,ppval(pp,xq))
line([4 4],ylim,'LineStyle','--','Color','k')
line([10 10],ylim,'LineStyle','--','Color','k')

Figure contains an axes object. The axes object contains 3 objects of type line.

打开实时脚本

创建并绘制一个具有四个区间的分段多项式，这四个区间中，两个二次多项式交替出现。

前两个子图显示了一个二次多项式在 [-8,-4] 区间上的结果以及它在 [-4,0] 区间上的求反。多项式为

1-(x2-1)2=-x24+x.

第三个子图显示将这两个二次多项式扩展到四个区间形成的分段多项式。添加垂直线是为了显示多项式汇合的点。

subplot(2,2,1)
cc = [-1/4 1 0]; 
pp1 = mkpp([-8 -4],cc);
xx1 = -8:0.1:-4; 
plot(xx1,ppval(pp1,xx1),'k-')

subplot(2,2,2)
pp2 = mkpp([-4 0],-cc);
xx2 = -4:0.1:0; 
plot(xx2,ppval(pp2,xx2),'k-')

subplot(2,1,2)
pp = mkpp([-8 -4 0 4 8],[cc;-cc;cc;-cc]);
xx = -8:0.1:8;
plot(xx,ppval(pp,xx),'k-')
hold on
line([-4 -4],ylim,'LineStyle','--')
line([0 0],ylim,'LineStyle','--')
line([4 4],ylim,'LineStyle','--')
hold off

Figure contains 3 axes objects. Axes object 1 contains an object of type line. Axes object 2 contains an object of type line. Axes object 3 contains 4 objects of type line.

输入参数

全部折叠

分段多项式，指定为结构体。可以使用 spline、pchip、makima、interp1 或样条工具函数 mkpp 创建 pp。

查询点，指定为向量或数组。xq 指定 ppval 在其处计算分段多项式的点。

数据类型: single | double

输出参量

全部折叠

查询点处的分段多项式值，以向量、矩阵或数组形式返回。

如果 pp 具有 [d1,..,dr] 值系数（非标量系数值），则：

  • 当 xq 是长度为 N 的向量时，v 的大小为 [d1,...,dr,N]，并且 v(:,...,:,j) 是在 xq(j) 处的值。

  • 当 xq 的大小为 [N1,...,Ns] 时，v 的大小为 [d1,...,dr,N1,...,Ns]，并且 v(:,...,:, j1,...,js) 是在 xq(j1,...,js) 处的值。

扩展功能

全部展开

版本历史记录

在 R2006a 之前推出

另请参阅

| | |