Main Content

pchip

分段三次 Hermite 插值多项式 (PCHIP)

全页折叠

语法

p = pchip(x,y,xq)
pp = pchip(x,y)

说明

示例

p = pchip(x,y,xq) 返回与 xq 中的查询点对应的插值向量 p。p 的值由 x 和 y 的保形分段三次插值确定。

示例

pp = pchip(x,y) 返回一个分段多项式结构体以用于 ppval 和样条实用工具 unmkpp。

示例

全部折叠

打开实时脚本

将 spline、pchip 和 makima 为两个不同数据集生成的插值结果进行比较。这些函数都执行不同形式的分段三次 Hermite 插值。每个函数计算插值斜率的方式不同，因此它们在基础数据的平台区或波动处展现出不同行为。

对连接两个平台区的样本数据进行插值，并比较结果。创建由 x 值、点 y 处的函数值以及查询点 xq 组成的向量。使用 spline、pchip 和 makima 计算查询点处的插值。绘制查询点处的插值函数值以进行比较。

x = -3:3; 
y = [-1 -1 -1 0 1 1 1]; 
xq1 = -3:.01:3;
p = pchip(x,y,xq1);
s = spline(x,y,xq1);
m = makima(x,y,xq1);
plot(x,y,'o',xq1,p,'-',xq1,s,'-.',xq1,m,'--')
legend('Sample Points','pchip','spline','makima','Location','SouthEast')

Figure contains an axes object. The axes object contains 4 objects of type line. One or more of the lines displays its values using only markers These objects represent Sample Points, pchip, spline, makima.

在本例中，pchip 和 makima 具有相似的行为，因为它们可以避免过冲，并且可以准确地连接平台区。

使用振动采样函数执行第二次比较。

x = 0:15;
y = besselj(1,x);
xq2 = 0:0.01:15;
p = pchip(x,y,xq2);
s = spline(x,y,xq2);
m = makima(x,y,xq2);
plot(x,y,'o',xq2,p,'-',xq2,s,'-.',xq2,m,'--')
legend('Sample Points','pchip','spline','makima')

Figure contains an axes object. The axes object contains 4 objects of type line. One or more of the lines displays its values using only markers These objects represent Sample Points, pchip, spline, makima.

当基础函数振荡时，spline 和 makima 能够比 pchip 更好地捕获点之间的移动，后者会在局部极值附近急剧扁平化。

打开实时脚本

创建 x 值及其函数值 y 的向量，然后使用 pchip 来构造一个分段多项式结构体。

x = -5:5;
y = [1 1 1 1 0 0 1 2 2 2 2];
p = pchip(x,y);

结合 ppval 使用该结构体以计算几个查询点处的插值。绘制结果。

xq = -5:0.2:5;
pp = ppval(p,xq);
plot(x,y,'o',xq,pp,'-.')
ylim([-0.2 2.2])

Figure contains an axes object. The axes object contains 2 objects of type line. One or more of the lines displays its values using only markers

输入参数

全部折叠

样本点，指定为一个向量。向量 x 指定提供数据 y 的点。x 的元素必须是唯一的。

数据类型： single | double

样本点处的函数值，指定为数值向量、矩阵或数组。x 和 y 的长度必须相同。

如果 y 是矩阵或数组，则在获取最后一个维度 y(:,...,:,j) 中的值时应使其匹配 x。在此情况下，y 的最后一个维度的长度必须与 x 相同。

数据类型： single | double

查询点，指定为标量、向量、矩阵或数组。xq 中指定的点是 pchip 计算出的插值函数值 yq 的 x 坐标。

数据类型： single | double

输出参数

全部折叠

查询点处的插值，以标量、向量、矩阵或数组形式返回。p 的大小与 y 和 xq 的大小相关：

  • 如果 y 为向量，则 p 的大小与 xq 相同。

  • 如果 y 是大小为 Ny = size(y) 的数组，则下列条件适用：

    • 如果 xq 为标量或向量，则 size(p) 返回 [Ny(1:end-1) length(xq)]。

    • 如果 xq 是数组，则 size(p) 返回 [Ny(1:end-1) size(xq)。

分段多项式，以结构体形式返回。将此结构体与 ppval 函数结合使用可计算一个或多个查询点处的插值多项式。该结构体包含以下字段。

字段描述
form

'pp'（分段多项式）

breaks

包含严格递增元素的长度为 L+1 的向量，这些元素代表 L 个区间中每个区间的开始点和结束点

coefs

L×k 矩阵，其中每行 coefs(i,:) 包含第 i 个区间 [breaks(i),breaks(i+1)] 上 k 次多项式的局部系数

pieces

段数 L

order

多项式的阶

dim

目标的维度

由于 coefs 中的多项式系数是每个区间的本地系数，因此您必须减去对应节点区间的较低端点，以使用传统多项式方程中的系数。换言之，对于区间 [x1,x2] 上的系数 [a,b,c,d]，对应的多项式为

f(x)=a(x−x1)3+b(x−x1)2+c(x−x1)+d .

详细信息

全部折叠

保形分段三次插值

pchip 使用具有以下属性的分段三次多项式 P(x) 进行插值：

  • 在每个子区间 xk≤x≤xk+1 上，多项式 P(x) 为应用于给定数据点的三次 Hermite 插值多项式，且在插值点具有指定的导数（斜率）。

  • P(x) 进行 y 插值，即 P(xj)=yj，并且该一阶导数 dPdx 是连续的。二阶导数 d2Pdx2 可能不连续，因此 xj 处可能存在跳跃。

  • 三次插值 P(x) 具有保形效果。在 xj 处的斜率以特定方式选择，使得 P(x) 保留数据的形状和相应的单调性。因此，在数据具有单调性的区间上，P(x) 也是单调的；在数据具有局部极值的点上，P(x) 也具有局部极值。

注意

如果 y 是矩阵，则 P(x) 在 y 的每一行上满足上述属性。

提示

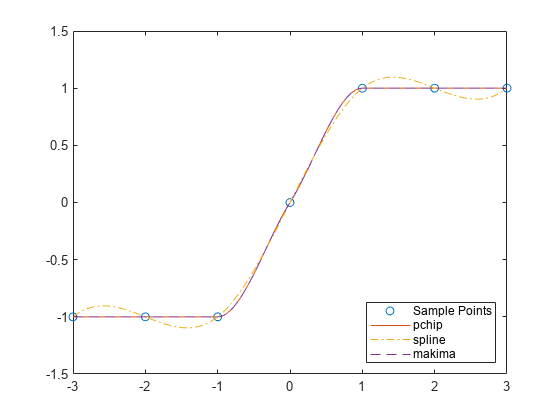
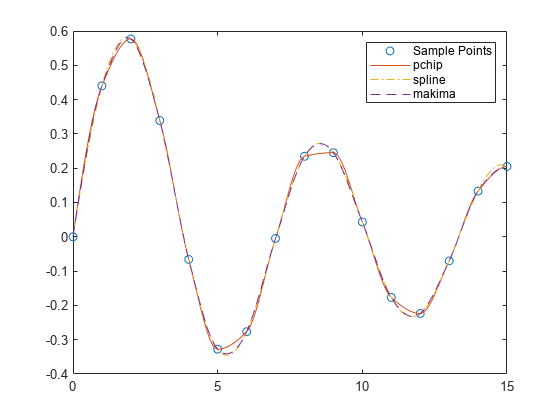
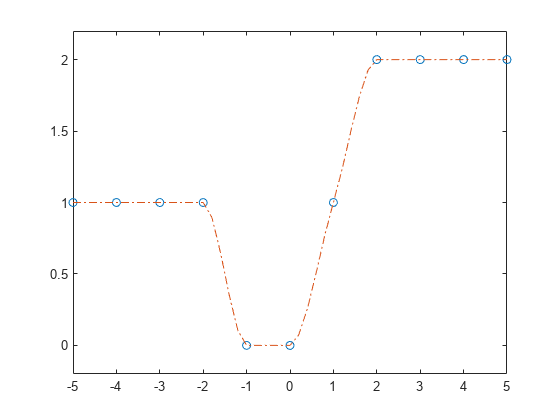
  • spline 构造 S(x) 的方式几乎与 pchip 构造 P(x) 的方式相同。但是，spline 在 xj 处选择斜率的方式不同，使得 S″(x) 是连续的。这种差异有几种效果：

    • spline 产生更平滑的结果，即 S″(x) 是连续的。

    • 如果数据由平滑函数的值组成，则 spline 可获得更精确的结果。

    • 如果数据不平滑，则 pchip 无过冲且振荡较少。

    • 设置 pchip 的开销较低。

    • 计算二者的开销相当。

参考

[1] Fritsch, F. N. and R. E. Carlson. "Monotone Piecewise Cubic Interpolation." SIAM Journal on Numerical Analysis. Vol. 17, 1980, pp.238–246.

[2] Kahaner, David, Cleve Moler, Stephen Nash. Numerical Methods and Software. Upper Saddle River, NJ: Prentice Hall, 1988.

扩展功能

版本历史记录

在 R2006a 之前推出

另请参阅

| | |