Main Content

fittype

Fit type for curve and surface fitting

collapse all in page

Syntax

aFittype = fittype(libraryModelName)
aFittype = fittype(expression)
aFittype = fittype(expression,Name,Value)
aFittype = fittype(linearModelTerms)
aFittype = fittype(linearModelTerms,Name,Value)
aFittype = fittype(anonymousFunction)
aFittype = fittype(anonymousFunction,Name,Value)

Description

aFittype = fittype(libraryModelName) creates the fittype object aFittype for the model specified by libraryModelName.

example

aFittype = fittype(expression) creates a fit type for the model specified by the MATLAB® expression.

aFittype = fittype(expression,Name,Value) constructs the fit type with additional options specified by one or more Name,Value pair arguments.

example

aFittype = fittype(linearModelTerms) creates a fit type for a custom linear model with terms specified by the expressions in linearModelTerms.

example

aFittype = fittype(linearModelTerms,Name,Value) constructs the fit type with additional options specified by one or more Name,Value pair arguments.

example

aFittype = fittype(anonymousFunction) creates a fit type for the model specified by anonymousFunction.

example

aFittype = fittype(anonymousFunction,Name,Value) constructs the fit type with additional options specified by one or more Name,Value pair arguments.

example

Examples

collapse all

Open Live Script

Construct fit types by specifying library model names.

Construct a fittype object for the cubic polynomial library model. 

f = fittype('poly3')
f = 
     Linear model Poly3:
     f(p1,p2,p3,p4,x) = p1*x^3 + p2*x^2 + p3*x + p4

Construct a fit type for the library model rat33 (a rational model of the third degree for both the numerator and denominator). 

f = fittype('rat33')
f = 
     General model Rat33:
     f(p1,p2,p3,p4,q1,q2,q3,x) = (p1*x^3 + p2*x^2 + p3*x + p4) /
               (x^3 + q1*x^2 + q2*x + q3)

For a list of library model names, see libraryModelName.

Open Live Script

Create a fit type for a custom nonlinear model, designating n as the problem-dependent parameter and u as the independent variable. 

g = fittype("n*u^a",...
            problem="n",...
            independent="u")
g = 
     General model:
     g(a,n,u) = n*u^a

Create a fit type for a logarithmic fit to some data, use the fit type to create a fit, and then plot the fit. 

x = linspace(1,100);  
y = 7*log(x+5);
myfittype = fittype("a*log(x+b)",...
    dependent="y",independent="x",...
    coefficients=["a" "b"])
myfittype = 
     General model:
     myfittype(a,b,x) = a*log(x+b)

myfit = fit(x',y',myfittype)
Warning: Start point not provided, choosing random start point.

myfit = 
     General model:
     myfit(x) = a*log(x+b)
     Coefficients (with 95% confidence bounds):
       a =           7  (7, 7)
       b =           5  (5, 5)

plot(myfit,x,y)

Figure contains an axes object. The axes object with xlabel x, ylabel y contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent Data, Fitted curve.

The plot shows that the fit follows the data.

Open Live Script

To use a linear fitting algorithm, specify a cell array of terms.

Identify the linear model terms you need to input to fittype: a*x + b*sin(x) + c. The model is linear in a, b and c. It has three terms x, sin(x) and 1 (because c=c*1). To specify this model you use this cell array of terms: LinearModelTerms = {'x','sin(x)','1'}.

Use the cell array of linear model terms as the input to fittype. 

ft = fittype({'x','sin(x)','1'})
ft = 
     Linear model:
     ft(a,b,c,x) = a*x + b*sin(x) + c

Create a linear model fit type for a*cos(x) + b. 

ft2 = fittype({'cos(x)','1'})
ft2 = 
     Linear model:
     ft2(a,b,x) = a*cos(x) + b

Create the fit type again and specify coefficient names. 

ft3 = fittype({'cos(x)','1'},'coefficients',{'a1','a2'})
ft3 = 
     Linear model:
     ft3(a1,a2,x) = a1*cos(x) + a2
Open Live Script

Define a function in a file and use it to create a fit type and fit a curve.

Define a function in a MATLAB® file.

type piecewiseLine.m
function y = piecewiseLine(x,a,b,c,k)
% PIECEWISELINE   A line made of two pieces

y = zeros(size(x));

% This example includes a for-loop and if statement
% purely for example purposes.
for i = 1:length(x)
    if x(i) < k
        y(i) = a + b.*x(i);
    else
        y(i) = a + b*k + c.*(x(i)-k); 
    end
end
end

Save the file.

Define some data and create a fit type specifying the function piecewiseLine.

x = [0.81;0.91;0.13;0.91;0.63;0.098;0.28;0.55;...
    0.96;0.96;0.16;0.97;0.96];
y = [0.17;0.12;0.16;0.0035;0.37;0.082;0.34;0.56;...
    0.15;-0.046;0.17;-0.091;-0.071];
ft = fittype('piecewiseLine( x, a, b, c, k )')
ft = 
     General model:
     ft(a,b,c,k,x) = piecewiseLine( x, a, b, c, k )

The inputs to ft are the coefficients in alphabetical order, followed by the independent variables. See Input Order for Anonymous Functions to learn more.

If you want to control the order of coefficients, then use an anonymous function input. For example, to change the order of the a and b coefficients:

ft = fittype(@(b,a,c,k,x) piecewiseLine(x,a,b,c,k))

You must specify the independent variable x last.

Create a fit using the fit type ft and plot the results.

f = fit(x, y, ft, 'StartPoint', [1, 0, 1, 0.5]);
plot(f, x, y)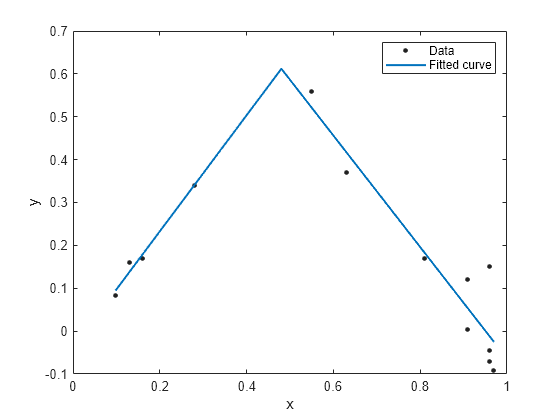

Figure contains an axes object. The axes object with xlabel x, ylabel y contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent Data, Fitted curve.

Create a fit type using an anonymous function.

g = fittype( @(a, b, c, x) a*x.^2+b*x+c )

Create a fit type using an anonymous function and specify independent and dependent parameters.

g = fittype( @(a, b, c, d, x, y) a*x.^2+b*x+c*exp(...
 -(y-d).^2 ), 'independent', {'x', 'y'},...
     'dependent', 'z' );

Create a fit type for a surface using an anonymous function and specify independent and dependent parameters, and problem parameters that you will specify later when you call fit.

g = fittype( @(a,b,c,d,x,y) a*x.^2+b*x+c*exp( -(y-d).^2 ), ...
        'problem', {'c','d'}, 'independent', {'x', 'y'}, ...
        'dependent', 'z' );

Use an anonymous function to pass workspace data into the fittype and fit functions.

Create and plot an S-shaped curve. In later steps, you stretch and move this curve to fit to some data.

% Breakpoints.
xs = (0:0.1:1).';
% Height of curve at breakpoints.
ys = [0; 0; 0.04; 0.1; 0.2; 0.5; 0.8; 0.9; 0.96; 1; 1];
% Plot S-shaped curve.
xi = linspace( 0, 1, 241 );
plot( xi, interp1( xs, ys, xi, 'pchip' ), 'LineWidth', 2 )
hold on
plot( xs, ys, 'o', 'MarkerFaceColor', 'r' )
hold off
title S-curve

Create a fit type using an anonymous function, taking the values from the workspace for the curve breakpoints (xs) and the height of the curve at the breakpoints (ys). Coefficients are b (base) and h (height).

ft = fittype( @(b, h, x) interp1( xs, b+h*ys, x, 'pchip' ) )

Plot the fittype specifying example coefficients of base b=1.1 and height h=-0.8. 

plot( xi, ft( 1.1, -0.8, xi ), 'LineWidth', 2 )
title 'Fittype with b=1.1 and h=-0.8'

Load and fit some data, using the fit type ft created using workspace values.

% Load some data
xdata = [0.012;0.054;0.13;0.16;0.31;0.34;0.47;0.53;0.53;...
   0.57;0.78;0.79;0.93];
ydata = [0.78;0.87;1;1.1;0.96;0.88;0.56;0.5;0.5;0.5;0.63;...
   0.62;0.39];
% Fit the curve to the data
f = fit( xdata, ydata, ft, 'Start', [0, 1] )
% Plot fit
plot( f, xdata, ydata )
title 'Fitted S-curve'

This example shows the differences between using anonymous functions with problem parameters and workspace variable values.

Load data, create a fit type for a curve using an anonymous function with problem parameters, and call fit specifying the problem parameters.

% Load some data.
xdata = [0.098;0.13;0.16;0.28;0.55;0.63;0.81;0.91;0.91;...
    0.96;0.96;0.96;0.97];
ydata = [0.52;0.53;0.53;0.48;0.33;0.36;0.39;0.28;0.28;...
    0.21;0.21;0.21;0.2];

% Create a fittype that has a problem parameter.
g = fittype( @(a,b,c,x) a*x.^2+b*x+c, 'problem', 'c' )

% Examine coefficients. Observe c is not a coefficient.
coeffnames( g )

% Examine arguments. Observe that c is an argument.
argnames( g )

% Call fit and specify the value of c.
f1 = fit( xdata, ydata, g, 'problem', 0, 'StartPoint', [1, 2] )

% Note: Specify start points in the calls to fit to
% avoid warning messages about random start points
% and to ensure repeatability of results.

% Call fit again and specify a different value of c,
% to get a new fit.
f2 = fit( xdata, ydata, g, 'problem', 1, 'start', [1, 2] )

% Plot results. Observe the specified c constants
% do not make a good fit.
plot( f1, xdata, ydata )
hold on
plot( f2, 'b' )
hold off

Modify the previous example to create the same fits using workspace values for variables, instead of using problem parameters. Using the same data, create a fit type for a curve using an anonymous function with a workspace value for variable c:

% Remove c from the argument list.
try
    g = fittype( @(a,b,x) a*x.^2+b*x+c )
catch e
    disp( e.message )
end
% Observe error because now c is undefined.
% Define c and create fittype:
c = 0;
g1 = fittype( @(a,b,x) a*x.^2+b*x+c )

% Call fit (now no need to specify problem parameter).
f1 = fit( xdata, ydata, g1, 'StartPoint', [1, 2] )
% Note that this f1 is the same as the f1 above.
% To change the value of c, recreate the fittype.
c = 1;
g2 = fittype( @(a,b,x) a*x.^2+b*x+c ) % uses c = 1
f2 = fit( xdata, ydata, g2, 'StartPoint', [1, 2] )
% Note that this f2 is the same as the f2 above.
% Plot results
plot( f1, xdata, ydata )
hold on
plot( f2, 'b' )
hold off

Input Arguments

collapse all

Library model to fit, specified as a character vector or string scalar. This table shows some common examples.

Library Model Name

Description

'poly1'

Linear polynomial curve

'poly11'

Linear polynomial surface

'poly2'

Quadratic polynomial curve

'linearinterp'

Piecewise linear interpolation

'cubicinterp'

Piecewise cubic interpolation

'smoothingspline'

Smoothing spline (curve)

'lowess'

Local linear regression (surface)

'log10'

Base-10 logarithmic curve

'logistic4'

Four-parameter logistic curve

For a list of library model names, see Model Names and Equations.

Example: 'poly2'

Data Types: char | string

Model to fit, specified as a character vector or string scalar. You can specify any MATLAB command and therefore any .m file. See Fit a Curve Defined by a File.

Data Types: char | string

Model to fit, specified as a cell array of character vectors or a string array. Specify the model terms by the expressions in the character vectors or string scalars. Do not include coefficients in the expressions for the terms. See Linear Model Terms.

Data Types: cell

Model to fit, specified as an anonymous function. For details, see Input Order for Anonymous Functions.

Data Types: char

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: 'coefficients',{'a1','a2'}

Coefficient names, specified as the comma-separated pair consisting of 'coefficients' and a character vector, string scalar, cell array of character vectors, or string array. You can use multicharacter symbol names. You cannot use these names: i, j, pi, inf, nan, eps.

Data Types: char | string | cell

Dependent variable name, specified as the comma-separated pair consisting of 'dependent' and a character vector or string scalar. If you do not specify the dependent variable, the function assumes y is the dependent variable.

Data Types: char | string

Independent variable names, specified as the comma-separated pair consisting of 'independent' and a character vector, string scalar, cell array of character vectors, or string array. You can specify a maximum of two independent variables. If you do not specify the independent variable, the function assumes x is the independent variable.

Data Types: char | string | cell

Fit options, specified as the comma-separated pair consisting of 'options' and the name of a fitoptions object.

Problem-dependent (fixed) parameter names, specified as the comma-separated pair consisting of 'problem' and a character vector, string scalar, cell array of character vectors, or string array with one element per problem dependent constant.

Data Types: char | string | cell

Output Arguments

collapse all

Model to fit, returned as a fittype. A fittype encapsulates information describing a model. To create a fit, you need data, a fittype, and (optionally) fitoptions and an exclusion rule. You can use a fittype as an input to the fit function.

More About

collapse all

Dependent and Independent Variables

How do I decide which variables are dependent and independent?

To determine dependent and independent variables and coefficients, consider this equation:

y=f(x)=a+(b*x)+(c*x2).

  • y is the dependent variable.

  • x is the independent variable.

  • a, b, and c are the coefficients.

The 'independent' variable is what you control. The 'dependent' variable is what you measure, i.e., it depends on the independent variable. The 'coefficients' are the parameters that the fitting algorithm estimates.

For example, if you have census data, then the year is the independent variable because it does not depend on anything. Population is the dependent variable, because its value depends on the year in which the census is taken. If a parameter like growth rate is part of the model, so the fitting algorithm estimates it, then the parameter is one of the 'coefficients'.

The fittype function determines input arguments by searching the fit type expression input for variable names. fittype assumes x is the independent variable, y is the dependent variable, and all other variables are coefficients of the model. x is used if no variable exists.

Input Order for Anonymous Functions

If the fit type expression input is an anonymous function, then the order of inputs must be correct. The input order enables the fittype function to determine which inputs are coefficients to estimate, problem-dependent parameters, and independent variables.

The order of the input arguments to the anonymous function must be:

fcn = @(coefficients,problemparameters,x,y) expression
You need at least one coefficient. The problem parameters and y are optional. The last arguments, x and y, represent the independent variables: just x for curves, but x and y for surfaces. If you don't want to use x and/or y to name the independent variables, then specify different names using the 'independent' argument name-value pair. However, whatever name or names you choose, these arguments must be the last arguments to the anonymous function.

Anonymous functions make it easier to pass other data into the fittype and fit functions.

  1. Create a fit type using an anonymous function and a variable value (c) from the workspace.

    c = 1;
 g = fittype( @(a, b, x) a*x.^2+b*x+c )

  2. The fittype function can use the variable values in your workspace when you create the fit type. To pass in new data from the workspace, recreate the fit type, e.g.,

    c = 5 % Change value of c.
g = fittype( @(a, b, x) a*x.^2+b*x+c )

  3. Here, the value of c is fixed when you create the fit type. To specify the value of c at the time you call fit, you can use problem parameters. For example, make a fit with c = 2 and then a new fit with c = 3.

    g = fittype( @(a,b,x,c) a*x.^2+b*x+c, 'problem', 'c' )
f1 = fit( xdata, ydata, g, 'problem', 2 )
f2 = fit( xdata, ydata, g, 'problem', 3 )

Linear Model Terms

How do I define linear model terms?

To use a linear fitting algorithm, specify linearModelTerms as a cell array or string array of terms. For example:

afittype = fittype({expr1,...,exprn})
Specify the model terms by the expressions in the character vectors expr2,...,exprn. Do not include coefficients in the expressions for the terms. If there is a constant term, use '1' as the corresponding expression in the cell array.

To specify a linear model of the following form: 

 coeff1 * term1 + coeff2 * term2 + coeff3 * term3 + ...
where no coefficient appears within any of term1, term2, etc., use a cell array or string array where each term, without coefficients, is specified in a cell or element of expr, as follows:
LinearModelTerms = {'term1', 'term2', 'term3', ... }

For example, the model 

a*x + b*sin(x) + c
is linear in a, b, and c. It has three terms x, sin(x) and 1 (because c=c*1) and therefore expr is:
LinearModelTerms = {'x','sin(x)','1'}

In the Curve Fitter app, select a Linear Fitting fit in the Custom group in the Fit Type section.

Algorithms

If the fit type expression input is a character vector, string scalar, or anonymous function, then the toolbox uses a nonlinear fitting algorithm to fit the model to data.

If the fit type expression input is a cell array or string array of terms, then the toolbox uses a linear fitting algorithm to fit the model to data.

Version History

Introduced before R2006a

expand all

See Also

Functions

Apps

Topics