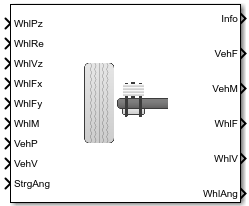
Solid Axle Suspension - Leaf Spring

Solid axle suspension with leaf spring

Libraries:
Vehicle Dynamics Blockset / Suspension

Description

The Solid Axle Suspension - Leaf Spring block implements a solid axle suspension with a leaf spring for multiple axles with multiple wheels per axle.

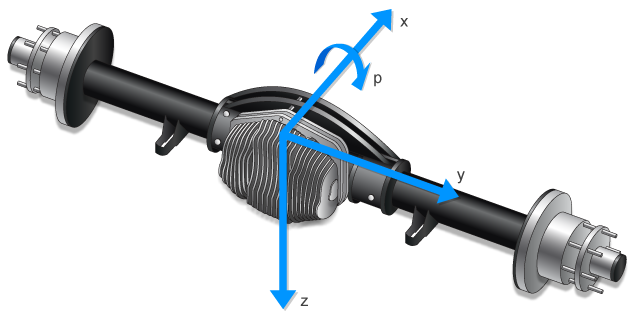
The block models the suspension compliance, damping, and geometric effects as functions of the wheel positions and velocities, with axle-specific compliance and damping parameters. Using the wheel position and velocity, the block calculates the vertical wheel position and suspension forces on the vehicle and wheel. The block uses the Z-down coordinate system (defined in SAE J670) and a solid axle coordinate system. The solid axle coordinate system is aligned with the Z-down vehicle coordinate system, with the x-axis in the direction of forward vehicle motion.

Illustration of a solid axle

This table describes the settings you can specify for each suspension element.

Suspension Element	Setting
Axle	Multiple wheels Suspension parameters
Wheel	Steering angles

Suspension Element

Setting

Axle

Multiple wheels
Suspension parameters

Wheel

Steering angles

The block contains energy-storing spring elements and energy-dissipating damper elements. The block also stores energy via the axle roll angular acceleration and axle center of mass vertical and lateral acceleration.

This table summarizes the block parameter settings for a vehicle with:

Two axles
Two wheels per axle
Steering angle input for both wheels on the front axle

Parameter	Setting
Number of axles, NumAxl	`2`
Number of wheels by axle, NumWhlsByAxl	`[2 2]`
Steered axle enable by axle, StrgEnByAxl	`[1 0]`

The block uses the wheel number, t, to index the input and output signals. This table summarizes the wheel, axle, and corresponding wheel number for a vehicle with:

Two axles
Two wheels per axle

Wheel	Axle	Wheel Number
Front left	Front	`1`
Front right	Front	`2`
Rear left	Rear	`1`
Rear right	Rear	`2`

Suspension Compliance and Damping

The block uses a linear spring and damper to model the vertical dynamic effects of the suspension system on the vehicle and wheel. Specifically, the block:

Uses	To Calculate
Longitudinal and lateral displacement and velocity of the vehicle. Longitudinal and lateral displacement and velocity of the wheel. Vertical wheel forces applied to the vehicle.	Suspension forces applied to the axle center. Vertical displacements and velocities of the vehicle and wheel. Longitudinal, lateral and vertical suspension forces and moments applied to the vehicle. Longitudinal, lateral and vertical suspension forces and moments applied to the wheel.

To calculate the dynamics of the axle, the block implements these equations. The block neglects the effects of:

Lateral and longitudinal translational velocity.
Angular velocity about the vertical and lateral axes.

$\begin{array}{l} [\begin{matrix} {\ddot{x}}_{a} \\ {\ddot{y}}_{a} \\ {\ddot{z}}_{a} \end{matrix}] = \frac{1}{M_{a}} [\begin{matrix} F_{x a} \\ F_{y a} \\ F_{z a} \end{matrix}] + [\begin{matrix} {\dot{x}}_{a} \\ {\dot{y}}_{a} \\ {\dot{z}}_{a} \end{matrix}] \times [\begin{matrix} p \\ q \\ r \end{matrix}] = \frac{1}{M_{a}} [\begin{matrix} 0 \\ 0 \\ F_{z a} \end{matrix}] + [\begin{matrix} 0 \\ 0 \\ {\dot{z}}_{a} \end{matrix}] \times [\begin{matrix} p \\ 0 \\ 0 \end{matrix}] + [\begin{matrix} 0 \\ 0 \\ g \end{matrix}] = [\begin{matrix} 0 \\ p {\dot{z}}_{a} \\ \frac{F_{z a}}{M_{a}} + g \end{matrix}] \\ [\begin{matrix} \dot{p} \\ \dot{q} \\ \dot{r} \end{matrix}] = [[\begin{matrix} M_{x} \\ M_{y} \\ M_{z} \end{matrix}] - [\begin{matrix} p \\ q \\ r \end{matrix}] \times [\begin{matrix} I_{x x} & 0 & 0 \\ 0 & I_{y y} & 0 \\ 0 & 0 & I_{z z} \end{matrix}] [\begin{matrix} p \\ q \\ r \end{matrix}]] {[\begin{matrix} I_{x x} & 0 & 0 \\ 0 & I_{y y} & 0 \\ 0 & 0 & I_{z z} \end{matrix}]}^{- 1} \\ = [[\begin{matrix} M_{x} \\ 0 \\ 0 \end{matrix}] - [\begin{matrix} p \\ q \\ 0 \end{matrix}] \times [\begin{matrix} I_{x x} & 0 & 0 \\ 0 & I_{y y} & 0 \\ 0 & 0 & I_{z z} \end{matrix}] [\begin{matrix} p \\ 0 \\ 0 \end{matrix}]] {[\begin{matrix} I_{x x} & 0 & 0 \\ 0 & I_{y y} & 0 \\ 0 & 0 & I_{z z} \end{matrix}]}^{- 1} = [\begin{matrix} \frac{M_{x}}{I_{x x}} \\ 0 \\ 0 \end{matrix}] \end{array}$

The net vertical force on the axle center of mass is the sum of the wheel and suspension forces acting on the axle.

$F_{z a} = \sum_{t = 1}^{N t a} (F_{w z_{a, t}} + F_{z 0_{a}} + k_{z_{a}} (z_{v_{a, t}} - z_{s_{a, t}} + m_{h s t e e r_{a}} | δ_{s t e e r_{a, t}} |) + c_{z_{a}} ({\dot{z}}_{v_{a, t}} - {\dot{z}}_{s_{a, t}}))$

The net moment about the roll axis of the solid axle suspension accounts for the hardpoint coordinates of the suspension and wheels.

$M_{x} = \sum_{t = 1}^{N t a} (F_{w z_{a, t}} y_{w_{t}} + (F_{z 0_{a}} + k_{z_{a}} (z_{v_{a, t}} - z_{s_{a, t}} + m_{h s t e e r_{a}} | δ_{s t e e r_{a, t}} |) + c_{z_{a}} ({\dot{z}}_{v_{a, t}} - {\dot{z}}_{s_{a, t}})) y_{s_{t}} + M_{w x_{a, t}} \frac{I_{x x}}{I_{x x} + M_{a} y_{w_{t}}})$

Block parameters provide the track and suspension hardpoints coordinates.

$\begin{array}{l} T c_{t} = [\begin{matrix} x_{w_{1}} & x_{w_{2}} & \dots \\ y_{w_{1}} & y_{w_{2}} & \dots \\ z_{w_{1}} & z_{w_{2}} & \dots \end{matrix}] \\ S c_{t} = [\begin{matrix} x_{s_{1}} & x_{s_{2}} & \dots \\ y_{s_{1}} & y_{s_{2}} & \dots \\ z_{s_{1}} & z_{s_{2}} & \dots \end{matrix}] \end{array}$

The block uses Euler angles to transform the track and suspension displacements, velocities, and accelerations to the vehicle coordinate system.

To calculate the suspension forces applied to the vehicle, the block implements this equation.

$F_{v z_{a, t} = -} (F_{z 0_{a}} + k_{z_{a}} (z_{v_{a, t}} - z_{s_{a, t}} + m_{h s t e e r_{a}} | δ_{s t e e r_{a, t}} |) + c_{z_{a}} ({\dot{z}}_{v_{a, t}} - {\dot{z}}_{s_{a, t}}) + F_{z h s t o p_{a, t}})$

The suspension forces and moments applied to the vehicle are equal to the suspension forces and moments applied to the wheel.

$\begin{array}{l} F_{v x_{a, t}} = F_{w x_{a, t}} \\ F_{v y_{a, t}} = F_{w y_{a, t}} \\ F_{v z_{a, t}} = - F_{w z_{a, t}} \\ M_{v x_{a, t}} = M_{w x_{a, t}} + F_{w y_{a, t}} (R e_{w y_{a, t}} + H_{a, t}) \\ M_{v y_{a, t}} = M_{w y_{a, t}} + F_{w x_{a, t}} (R e_{w x_{a, t}} + H_{a, t}) \\ M_{v z_{a, t}} = M_{w z_{a, t}} \end{array}$

To calculate the vertical force applied to the suspension at the wheel location, the block implements a stiff spring-damper, shown here.

Illustration of a spring damper on a solid axle.

The block uses this equation.

$F_{w z_{a, t}} = - F w a_{z 0} - k w a_{z} (z_{w_{a, t}} - z_{s_{a, t}}) - c w a_{z} ({\dot{z}}_{w_{a, t}} - {\dot{z}}_{s_{a, t}})$

The equations use these variables.

F_{wz_a,t}, M_{wz_a,t}	Suspension force and moment applied to the wheel on axle `a`, wheel `t` along wheel-fixed z-axis
F_{wx_a,t}, M_{wx_a,t}	Suspension force and moment applied to the wheel on axle `a`, wheel `t` along wheel-fixed x-axis
F_{wy_a,t}, M_{wy_a,t}	Suspension force and moment applied to the wheel on axle `a`, wheel `t` along wheel-fixed y-axis
F_{vz_a,t}, M_{vz_a,t}	Suspension force and moment applied to the vehicle on axle `a`, wheel `t` along wheel-fixed z-axis
F_{vx_a,t}, M_{vx_a,t}	Suspension force and moment applied to the vehicle on axle `a`, wheel `t` along wheel-fixed x-axis
F_{vy_a,t}, M_{vy_a,t}	Suspension force and moment applied to the vehicle on axle `a`, wheel `t` along wheel-fixed y-axis
F_{z0_a}	Vertical suspension spring preload force applied to the wheels on axle `a`
k_{z_a}	Vertical spring constant applied to wheels on axle `a`
kwa_z	Wheel and axle interface compliance constant
m_{hsteer_a}	Steering angle to vertical force slope applied at wheel carrier for wheels on axle `a`
δ_{steer_a,t}	Steering angle input for axle `a`, wheel `t`
c_{z_a}	Vertical damping constant applied to wheels on axle `a`
cwa_z	Wheel and axle interface damping constant
Re_{w_a,t}	Effective wheel radius for axle `a`, wheel `t`
F_{zhstop_a,t}	Vertical hardstop force at axle `a`, wheel `t`, along the inertial-fixed z-axis
F_{zaswy_a,t}	Vertical anti-sway force at axle `a`, wheel `t`, along the inertial-fixed z-axis
Fwa_z0	Wheel and axle interface compliance constant
z_{v_a,t}, ż_{v_a,t}	Vehicle displacement and velocity at axle `a`, wheel `t`, along the inertial-fixed z-axis
z_{w_a,t}, ż_{w_a,t}	Wheel displacement and velocity at axle `a`, wheel `t`, along the inertial-fixed z-axis
x_{v_a,t}, ẋ_{v_a,t}	Vehicle displacement and velocity at axle `a`, wheel `t`, along the inertial-fixed z-axis
x_{w_a,t}, ẋ_{w_a,t}	Wheel displacement and velocity at axle `a`, wheel `t`, along the inertial-fixed z-axis
y_{v_a,t}, ẏ_{v_a,t}	Vehicle displacement and velocity at axle `a`, wheel `t`, along the inertial-fixed y-axis
y_{w_a,t}, ẏ_{w_a,t}	Wheel displacement and velocity at axle `a`, wheel `t`, along the inertial-fixed y-axis
H_a,t	Suspension height at axle `a`, wheel `t`
Re_{w_a,t}	Effective wheel radius at axle `a`, wheel `t`

Hardstop Forces

The hardstop feedback force, F_{zhstop_a,t}, that the block applies depends on whether the suspension is compressing or extending. The block applies the force:

In compression, when the suspension is compressed more than the maximum distance specified by the Suspension maximum height, Hmax parameter
In extension, when the suspension extension is greater than maximum extension specified by the Suspension maximum height, Hmax parameter

To calculate the force, the block uses a stiffness based on a hyperbolic tangent and exponential scaling.

Camber, Caster, and Toe Angles

To calculate the camber, caster, and toe angles, block uses linear functions of the suspension height and steering angle.

$\begin{array}{l} ξ_{a, t} = ξ_{0 a} + m_{h c a m b e r_{a}} (z_{w_{a, t}} - z_{v_{a, t}} - m_{h s t e e r_{a}} | δ_{s t e e r_{a, t}} |) + m_{c a m b e r s t e e r_{a}} | δ_{s t e e r_{a, t}} | \\ η_{a, t} = η_{0 a} + m_{h c a s t e r_{a}} (z_{w_{a, t}} - z_{v_{a, t}} - m_{h s t e e r_{a}} | δ_{s t e e r_{a, t}} |) + m_{c a s t e r s t e e r_{a}} | δ_{s t e e r_{a, t}} | \\ ζ_{a, t} = ζ_{0 a} + m_{h t o e_{a}} (z_{w_{a, t}} - z_{v_{a, t}} - m_{h s t e e r_{a}} | δ_{s t e e r_{a, t}} |) + m_{t o e s t e e r_{a}} | δ_{s t e e r_{a, t}} | \end{array}$

The equations use these variables.

ξ_a,t	Camber angle of wheel on axle `a`, wheel `t`
η_a,t	Caster angle of wheel on axle `a`, wheel `t`
ζ_a,t	Toe angle of wheel on axle `a`, wheel `t`
ξ_0a, η_0a, ζ_0a	Nominal suspension axle a camber, caster, and toe angles, respectively, at zero steering angle
m_{hcamber_a}, m_{hcaster_a}, m_{htoe_a}	Camber, caster, and toe angles, respectively, versus suspension height slope for axle `a`
m_{cambersteer_a}, m_{castersteer_a}, m_{toesteer_a}	Camber, caster, and toe angles, respectively, versus steering angle slope for axle `a`
m_{hsteer_a}	Steering angle versus vertical force slope for axle `a`
δ_{steer_a,t}	Steering angle input for axle `a`, wheel `t`
z_{v_a,t}	Vehicle displacement at axle `a`, wheel `t`, along the inertial-fixed z-axis
z_{w_a,t}	Wheel displacement at axle `a`, wheel `t`, along the inertial-fixed z-axis

Steering Angles

Optionally, use the Steered axle enable by axle, StrgEnByAxl parameter to input steering angles for the wheels. To calculate the steering angles for the wheels, the block offsets the input steering angles with a linear function of the suspension height.

$δ_{w h l s t e e r_{a, t}} = δ_{s t e e r_{a, t}} + m_{h t o e_{a}} (z_{w_{a, t}} - z_{v_{a, t}} - m_{h s t e e r_{a}} | δ_{s t e e r_{a, t}} |) + m_{t o e s t e e r_{a}} | δ_{s t e e r_{a, t}} |$

The equation uses these variables.

m_{toesteer_a}	Axle `a` toe angle versus steering angle slope
m_{hsteer_a}	Axle `a` steering angle versus vertical force slope
m_{htoe_a}	Axle `a` toe angle versus suspension height slope
δ_{whlsteer_a,t}	Wheel steering angle for axle `a`, wheel `t`
δ_{steer_a,t}	Steering angle input for axle `a`, wheel `t`
z_{v_a,t}	Vehicle displacement at axle `a`, wheel `t`, along the inertial-fixed z-axis
z_{w_a,t}	Wheel displacement at axle `a`, wheel `t`, along the inertial-fixed z-axis

Power and Energy

The block calculates these suspension characteristics for each axle, a, wheel, t.

Calculation	Equation
Dissipated power, P_{susp_a,t}	$P_{s u s p_{a, t}} = F_{w z l o o k u p_{a}} ({\dot{z}}_{v_{a, t}} - {\dot{z}}_{w_{a, t}}, {\dot{z}}_{v_{a, t}} - {\dot{z}}_{w_{a, t}}, δ_{s t e e r_{a, t}})$
Absorbed energy, E_{susp_a,t}	$E_{s u s p_{a, t}} = F_{w z l o o k u p_{a}} ({\dot{z}}_{v_{a, t}} - {\dot{z}}_{w_{a, t}}, {\dot{z}}_{v_{a, t}} - {\dot{z}}_{w_{a, t}}, δ_{s t e e r_{a, t}})$
Suspension height, H_a,t	$H_{a, t} = - (z_{v_{a, t}} - z_{w_{a, t}} + \frac{F_{z 0_{a}}}{k_{z_{a}}} + m_{h s t e e r_{a}} \| δ_{s t e e r_{a, t}} \|)$
Distance from wheel carrier center to tire/road interface	$z_{w t r_{a, t}} = R e_{w_{a, t}} + H_{a, t}$

The equations use these variables.

m_{hsteer_a}	Steering angle to vertical force slope applied at wheel carrier for wheels on axle `a`
δ_{steer_a,t}	Steering angle input for axle `a`, wheel `t`
Re_{w_a,t}	Axle `a`, wheel `t` effective wheel radius from wheel carrier center to tire/road interface
F_{z0_a}	Vertical suspension spring preload force applied to the wheels on axle `a`
z_{wtr_a,t}	Distance from wheel carrier center to tire/road interface, along the inertial-fixed z-axis
z_{v_a,t}, ż_{v_a,t}	Vehicle displacement and velocity at axle `a`, wheel `t`, along the inertial-fixed z-axis
z_{w_a,t}, ż_{w_a,t}	Wheel displacement and velocity at axle `a`, wheel `t`, along the inertial-fixed z-axis

Examples

Kinematics and Compliance Virtual Test Laboratory Reference Application

Generate optimized suspension parameters for the vehicle dynamics mapped suspension blocks.

Open Script

Ports

Input

expand all

WhlPz — Wheel `z`-axis displacement
array

Wheel displacement, z_w, along wheel-fixed z-axis, in m. Array dimensions are 1 by the total number of wheels on the vehicle.

For example, for a two-axle vehicle with two wheels per axle, the WhlPz:

Signal array dimensions are [1x4].
$WhlPz = z_{w} = [\begin{matrix} z_{w_{1, 1}} & z_{w_{1, 2}} & z_{w_{2, 1}} & z_{w_{2, 2}} \end{matrix}]$
Wheel Array Element Axle Wheel Number
Front left WhlPz(1,1) 1 1
Front right WhlPz(1,2) 1 2
Rear left WhlPz(1,3) 2 1
Rear right WhlPz(1,4) 2 2

Wheel	Array Element	Axle	Wheel Number
Front left	`WhlPz(1,1)`	`1`	`1`
Front right	`WhlPz(1,2)`	`1`	`2`
Rear left	`WhlPz(1,3)`	`2`	`1`
Rear right	`WhlPz(1,4)`	`2`	`2`

WhlRe — Wheel effective radius
array

Effective wheel radius, Re_w, in m. Array dimensions are 1 by the total number of wheels on the vehicle.

For example, for a two-axle vehicle with two wheels per axle, the WhlRe:

Signal array dimensions are [1x4].
$Whl Re = R e_{w} = [\begin{matrix} R e_{w_{1, 1}} & R e_{w_{1, 2}} & R e_{w_{2, 1}} & R e_{w_{2, 2}} \end{matrix}]$
Wheel Array Element Axle Wheel Number
Front left WhlRe(1,1) 1 1
Front right WhlRe(1,2) 1 2
Rear left WhlRe(1,3) 2 1
Rear right WhlRe(1,4) 2 2

Wheel	Array Element	Axle	Wheel Number
Front left	`WhlRe(1,1)`	`1`	`1`
Front right	`WhlRe(1,2)`	`1`	`2`
Rear left	`WhlRe(1,3)`	`2`	`1`
Rear right	`WhlRe(1,4)`	`2`	`2`

WhlVz — Wheel `z`-axis velocity
array

Wheel velocity, ż_w, along wheel-fixed z-axis, in m. Array dimensions are 1 by the total number of wheels on the vehicle.

For example, for a two-axle vehicle with two wheels per axle, the WhlVz:

Signal array dimensions are [1x4].
$WhlVz = {\dot{z}}_{w} = [\begin{matrix} {\dot{z}}_{w_{1, 1}} & {\dot{z}}_{w_{1, 2}} & {\dot{z}}_{w_{2, 1}} & {\dot{z}}_{w_{2, 2}} \end{matrix}]$
Wheel Array Element Axle Wheel Number
Front left WhlVz(1,1) 1 1
Front right WhlVz(1,2) 1 2
Rear left WhlVz(1,3) 2 1
Rear right WhlVz(1,4) 2 2

Wheel	Array Element	Axle	Wheel Number
Front left	`WhlVz(1,1)`	`1`	`1`
Front right	`WhlVz(1,2)`	`1`	`2`
Rear left	`WhlVz(1,3)`	`2`	`1`
Rear right	`WhlVz(1,4)`	`2`	`2`

WhlFx — Longitudinal wheel force on vehicle
array

Longitudinal wheel force applied to vehicle, F_wx, along the inertial-fixed x-axis. Array dimensions are 1 by the total number of wheels on the vehicle.

For example, for a two-axle vehicle with two wheels per axle, the WhlFx:

Signal array dimensions are [1x4].
$WhlFx = F_{w x} = [\begin{matrix} F_{w x_{1, 1}} & F_{w x_{1, 2}} & F_{w x_{2, 1}} & F_{w x_{2, 2}} \end{matrix}]$
Wheel Array Element Axle Wheel Number
Front left WhlFx(1,1) 1 1
Front right WhlFx(1,2) 1 2
Rear left WhlFx(1,3) 2 1
Rear right WhlFx(1,4) 2 2

Wheel	Array Element	Axle	Wheel Number
Front left	`WhlFx(1,1)`	`1`	`1`
Front right	`WhlFx(1,2)`	`1`	`2`
Rear left	`WhlFx(1,3)`	`2`	`1`
Rear right	`WhlFx(1,4)`	`2`	`2`

WhlFy — Lateral wheel force on vehicle
array

Lateral wheel force applied to vehicle, F_wy, along the inertial-fixed y-axis. Array dimensions are 1 by the total number of wheels on the vehicle.

For example, for a two-axle vehicle with two wheels per axle, the WhlFy:

Signal array dimensions are [1x4].

$WhlFy = F_{w y} = [\begin{matrix} F_{w y_{1, 1}} & F_{w y_{1, 2}} & F_{w y_{2, 1}} & F_{w y_{2, 2}} \end{matrix}]$

Wheel Array Element Axle Wheel Number
Front left WhlFy(1,1) 1 1
Front right WhlFy(1,2) 1 2
Rear left WhlFy(1.3) 2 1
Rear right WhlFy(1,4) 2 2

Wheel	Array Element	Axle	Wheel Number
Front left	`WhlFy(1,1)`	`1`	`1`
Front right	`WhlFy(1,2)`	`1`	`2`
Rear left	`WhlFy(1.3)`	`2`	`1`
Rear right	`WhlFy(1,4)`	`2`	`2`

WhlM — Suspension moment on wheel
array

Longitudinal, lateral, and vertical suspension moments at axle a, wheel t, applied to the wheel at the axle wheel carrier reference coordinate, in N·m. Input array dimensions are 3 by the number of wheels on the vehicle.

WhlM(1,...) — Suspension moment applied to the wheel about the inertial-fixed x-axis (longitudinal)
WhlM(2,...) — Suspension moment applied to the wheel about the inertial-fixed y-axis (lateral)
WhlM(3,...) — Suspension moment applied to the wheel about the inertial-fixed z-axis (vertical)

For example, for a two-axle vehicle with two wheels per axle, the WhlM:

Signal dimensions are [3x4].

Signal contains suspension moments applied to four wheels according to their axle and wheel locations.

$WhlM = M_{w} = [\begin{matrix} M_{w x_{1, 1}} & M_{w x_{1, 2}} & M_{w x_{2, 1}} & M_{w x_{2, 2}} \\ M_{w y_{1, 1}} & M_{w y_{1, 2}} & M_{w y_{2, 1}} & M_{w y_{2, 2}} \\ M_{w z_{1, 1}} & M_{w z_{1, 2}} & M_{w z_{2, 1}} & M_{w z_{2, 2}} \end{matrix}]$

Wheel	Array Element	Axle	Wheel Number	Moment Axis
Front left	`WhlM(1,1)`	`1`	`1`	Inertial-fixed x-axis (longitudinal)
Front right	`WhlM(1,2)`	`1`	`2`
Rear left	`WhlM(1,3)`	`2`	`1`
Rear right	`WhlM(1,4)`	`2`	`2`
Front left	`WhlM(2,1)`	`1`	`1`	Inertial-fixed y-axis (lateral)
Front right	`WhlM(2,2)`	`1`	`2`
Rear left	`WhlM(2,3)`	`2`	`1`
Rear right	`WhlM(2,4)`	`2`	`2`
Front left	`WhlM(3,1)`	`1`	`1`	Inertial-fixed z-axis (vertical)
Front right	`WhlM(3,2)`	`1`	`2`
Rear left	`WhlM(3,3)`	`2`	`1`
Rear right	`WhlM(3,4)`	`2`	`2`

VehP — Vehicle displacement
array

Vehicle displacement from axle a, wheel t along inertial-fixed coordinate system, in m. Input array dimensions are 3 by the number of wheels on the vehicle.

VehP(1,...) — Vehicle displacement from wheel, x_v, along the inertial-fixed x-axis
VehP(2,...) — Vehicle displacement from wheel, y_v, along the inertial-fixed y-axis
VehP(3,...) — Vehicle displacement from wheel, z_v, along the inertial-fixed z-axis

For example, for a two-axle vehicle with two wheels per axle, the VehP:

Signal dimensions are [3x4].

Signal contains four displacements according to their axle and wheel locations.

$VehP = [\begin{matrix} x_{v} \\ y_{v} \\ z_{v} \end{matrix}] = [\begin{matrix} x_{v}_{_{1, 1}} & x_{v}_{_{1, 2}} & x_{v}_{_{2, 1}} & x_{v}_{_{2, 2}} \\ y_{v}_{_{1, 1}} & y_{v}_{_{1, 2}} & y_{v}_{_{2, 1}} & y_{v}_{_{2, 2}} \\ z_{v}_{_{1, 1}} & z_{v}_{_{1, 2}} & z_{v}_{_{2, 1}} & z_{v}_{_{2, 2}} \end{matrix}]$

Wheel	Array Element	Axle	Wheel Number	Axis
Front left	`VehP(1,1)`	`1`	`1`	Inertial-fixed x-axis
Front right	`VehP(1,2)`	`1`	`2`
Rear left	`VehP(1,3)`	`2`	`1`
Rear right	`VehP(1,4)`	`2`	`2`
Front left	`VehP(2,1)`	`1`	`1`	Inertial-fixed y-axis
Front right	`VehP(2,2)`	`1`	`2`
Rear left	`VehP(2,3)`	`2`	`1`
Rear right	`VehP(2,4)`	`2`	`2`
Front left	`VehP(3,1)`	`1`	`1`	inertial-fixed z-axis
Front right	`VehP(3,2)`	`1`	`2`
Rear left	`VehP(3,3)`	`2`	`1`
Rear right	`VehP(3,4)`	`2`	`2`

VehV — Vehicle velocity
array

Vehicle velocity at axle a, wheel t along inertial-fixed coordinate system, in m. Input array dimensions are 3 by the number of wheels on the vehicle.

VehV(1,...) — Vehicle velocity at wheel, x_v, along the inertial-fixed x-axis
VehV(2,...) — Vehicle velocity at wheel, y_v, along the inertial-fixed y-axis
VehV(3,...) — Vehicle velocity at wheel, z_v, along the inertial-fixed z-axis

For example, for a two-axle vehicle with two wheels per axle, the VehV:

Signal dimensions are [3x4].

Signal contains 4 velocities according to their axle and wheel locations.

$VehV = [\begin{matrix} {\dot{x}}_{v} \\ {\dot{y}}_{v} \\ {\dot{z}}_{v} \end{matrix}] = [\begin{matrix} {\dot{x}}_{v_{1, 1}} & {\dot{x}}_{v_{1, 2}} & {\dot{x}}_{v_{2, 1}} & {\dot{x}}_{v_{2, 2}} \\ {\dot{y}}_{v_{1, 1}} & {\dot{y}}_{v_{1, 2}} & {\dot{y}}_{v_{2, 1}} & {\dot{y}}_{v_{2, 2}} \\ {\dot{z}}_{v_{1, 1}} & {\dot{z}}_{v_{1, 2}} & {\dot{z}}_{v_{2, 1}} & {\dot{z}}_{v_{2, 2}} \end{matrix}]$

Wheel	Array Element	Axle	Wheel Number	Axis
Front left	`VehV(1,1)`	`1`	`1`	Inertial-fixed x-axis
Front right	`VehV(1,2)`	`1`	`2`
Rear left	`VehV(1,3)`	`2`	`1`
Rear right	`VehV(1,4)`	`2`	`2`
Front left	`VehV(2,1)`	`1`	`1`	Inertial-fixed y-axis
Front right	`VehV(2,2)`	`1`	`2`
Rear left	`VehV(2,3)`	`2`	`1`
Rear right	`VehV(2,4)`	`2`	`2`
Front left	`VehV(3,1)`	`1`	`1`	Inertial-fixed z-axis
Front right	`VehV(3,2)`	`1`	`2`
Rear left	`VehV(3,3)`	`2`	`1`
Rear right	`VehV(3,4)`	`2`	`2`

StrgAng — Steering angle, optional
array

Optional steering angle for each wheel, δ. Input array dimensions are 1 by the number of steered wheels.

For example, for a two-axle vehicle with two wheels per axle, you can input steering angles for both wheels on the first axle.

To enable the StrgAng port, set Steered axle enable by axle, StrgEnByAxl to [1 0]. The input signal array dimensions are [1x2].
The StrgAng signal contains two steering angles according to their axle and wheel locations.
$StrgAng = δ_{s t e e r} = [\begin{matrix} δ_{s t e e r_{1, 1}} & δ_{s t e e r_{1, 2}} \end{matrix}]$
Wheel Array Element Axle Wheel Number
Front left StrgAng(1,1) 1 1
Front right StrgAng(1,2) 1 2

Wheel	Array Element	Axle	Wheel Number
Front left	`StrgAng(1,1)`	`1`	`1`
Front right	`StrgAng(1,2)`	`1`	`2`

Dependencies

To enable the port StrgAng, set an element of the Steered axle enable by axle, StrgEnByAxl vector to 1.

Output

expand all

Info — Bus signal
bus

Bus signal containing block values. The signals are arrays that depend on the wheel location.

For example, these are the indices for a two-axle, two-wheel vehicle. The total number of wheels is four.

1D array signal (1-by-4)

Array Element Axle Wheel Number
(1,1) 1 1
(1,2) 1 2
(1,3) 2 1
(1,4) 2 2
3D array signal (3-by-4)

Array Element Axle Wheel Number
(1,1) 1 1
(1,2) 1 2
(1,3) 2 1
(1,4) 2 2
(2,1) 1 1
(2,2) 1 2
(2,3) 2 1
(2,4) 2 2
(3,1) 1 1
(3,2) 1 2
(3,3) 2 1
(3,4) 2 2

Array Element	Axle	Wheel Number
`(1,1)`	`1`	`1`
`(1,2)`	`1`	`2`
`(1,3)`	`2`	`1`
`(1,4)`	`2`	`2`

Array Element	Axle	Wheel Number
`(1,1)`	`1`	`1`
`(1,2)`	`1`	`2`
`(1,3)`	`2`	`1`
`(1,4)`	`2`	`2`
`(2,1)`	`1`	`1`
`(2,2)`	`1`	`2`
`(2,3)`	`2`	`1`
`(2,4)`	`2`	`2`
`(3,1)`	`1`	`1`
`(3,2)`	`1`	`2`
`(3,3)`	`2`	`1`
`(3,4)`	`2`	`2`

Signal	Description	Array Signal	Variable	Units
`Camber`	Wheel angles according to the axle.	1D	$WhlAng [1, ...] = ξ = [ξ_{a, t}]$	rad
`Caster`			$WhlAng [2, ...] = η = [η_{a, t}]$
`Toe`			$WhlAng [3, ...] = ζ = [ζ_{a, t}]$
`Height`	Suspension height	1D	H	m
`Power`	Suspension power dissipation	1D	P_susp	W
`Energy`	Suspension absorbed energy	1D	E_susp	J
`VehF`	Suspension forces applied to the vehicle	3D	For a two-axle, two wheels per axle vehicle: $VehF = F_{v} = [\begin{matrix} F_{v}_{x_{1, 1}} & F_{v}_{x_{1, 2}} & F_{v}_{x_{2, 1}} & F_{v}_{x_{2, 2}} \\ F_{v}_{y_{1, 1}} & F_{v}_{y_{1, 2}} & F_{v}_{y_{2, 1}} & F_{v}_{y_{2, 2}} \\ F_{v}_{z_{1, 1}} & F_{v}_{z_{1, 2}} & F_{v}_{z_{2, 1}} & F_{v}_{z_{2, 2}} \end{matrix}]$	N
`VehM`	Suspension moments applied to vehicle	3D	For a two-axle, two wheels per axle vehicle: $VehM = M_{v} = [\begin{matrix} M_{v x_{1, 1}} & M_{v x_{1, 2}} & M_{v x_{2, 1}} & M_{v x_{2, 2}} \\ M_{v y_{1, 1}} & M_{v y_{1, 2}} & M_{v y_{2, 1}} & M_{v y_{2, 2}} \\ M_{v z_{1, 1}} & M_{v z_{1, 2}} & M_{v z_{2, 1}} & M_{v z_{2, 2}} \end{matrix}]$	N·m
`WhlF`	Suspension force applied to wheel	3D	For a two-axle, two wheels per axle vehicle: $WhlF = F_{w} = [\begin{matrix} F_{w}_{x_{1, 1}} & F_{w}_{x_{1, 2}} & F_{w}_{x_{2, 1}} & F_{w}_{x_{2, 2}} \\ F_{w}_{y_{1, 1}} & F_{w}_{y_{1, 2}} & F_{w}_{y_{2, 1}} & F_{w}_{y_{2, 2}} \\ F_{w}_{z_{1, 1}} & F_{w}_{z_{1, 2}} & F_{w}_{z_{2, 1}} & F_{w}_{z_{2, 2}} \end{matrix}]$	N
`WhlP`	Wheel displacement	3D	For a two-axle, two wheels per axle vehicle: $WhlP = [\begin{matrix} x_{w} \\ y_{w} \\ z_{w} \end{matrix}] = [\begin{matrix} x_{w}_{_{1, 1}} & x_{w}_{_{1, 2}} & x_{w}_{_{2, 1}} & x_{w_{2, 2}} \\ y_{w}_{_{1, 1}} & y_{w}_{_{1, 2}} & y_{w}_{_{2, 1}} & y_{w}_{y_{2, 2}} \\ z_{w t r}_{_{1, 1}} & z_{w t r}_{_{1, 2}} & z_{w t r}_{_{2, 1}} & z_{w t r_{2, 2}} \end{matrix}]$	m
`WhlV`	Wheel velocity	3D	For a two-axle, two wheels per axle vehicle: $WhlV = [\begin{matrix} {\dot{x}}_{w} \\ {\dot{y}}_{w} \\ {\dot{z}}_{w} \end{matrix}] = [\begin{matrix} {\dot{x}}_{w_{1, 1}} & {\dot{x}}_{w_{1, 2}} & {\dot{x}}_{w_{2, 1}} & {\dot{x}}_{w_{2, 2}} \\ {\dot{y}}_{w_{_{1, 1}}} & {\dot{y}}_{w_{1, 2}} & {\dot{y}}_{w_{2, 1}} & {\dot{y}}_{w_{2, 2}} \\ {\dot{z}}_{w_{_{1, 1}}} & {\dot{z}}_{w_{1, 2}} & {\dot{z}}_{w_{2, 1}} & {\dot{z}}_{w_{2, 2}} \end{matrix}]$	m/s
`WhlAng`	Wheel camber, caster, toe angles	3D	For a two-axle, two wheels per axle vehicle: $WhlAng = [\begin{matrix} ξ \\ η \\ ζ \end{matrix}] = [\begin{matrix} ξ_{1, 1} & ξ_{1, 2} & ξ_{2, 1} & ξ_{2, 2} \\ η_{1, 1} & η_{1, 2} & η_{2, 1} & η_{2, 2} \\ ζ_{1, 1} & ζ_{1, 2} & ζ_{2, 1} & ζ_{2, 2} \end{matrix}]$	rad

VehF — Suspension force on vehicle
`array`

Longitudinal, lateral, and vertical suspension force at axle a, wheel t, applied to the vehicle at the suspension connection point, in N. Array dimensions are 3 by the number of wheels on the vehicle.

VehF(1,...) — Suspension force applied to vehicle along the inertial-fixed x-axis (longitudinal)
VehF(2,...) — Suspension force applied to vehicle along the inertial-fixed y-axis (lateral)
VehF(3,...) — Suspension force applied to vehicle along the inertial-fixed z-axis (vertical)

For example, for a two-axle vehicle with two wheels per axle, the VehF:

Signal dimensions are [3x4].

Signal contains suspension forces applied to the vehicle according to the axle and wheel locations.

$VehF = F_{v} = [\begin{matrix} F_{v}_{x_{1, 1}} & F_{v}_{x_{1, 2}} & F_{v}_{x_{2, 1}} & F_{v}_{x_{2, 2}} \\ F_{v}_{y_{1, 1}} & F_{v}_{y_{1, 2}} & F_{v}_{y_{2, 1}} & F_{v}_{y_{2, 2}} \\ F_{v}_{z_{1, 1}} & F_{v}_{z_{1, 2}} & F_{v}_{z_{2, 1}} & F_{v}_{z_{2, 2}} \end{matrix}]$

Wheel	Array Element	Axle	Wheel Number	Force Axis
Front left	`VehF(1,1)`	`1`	`1`	Inertial-fixed x-axis (longitudinal)
Front right	`VehF(1,2)`	`1`	`2`
Rear left	`VehF(1,3)`	`2`	`1`
Rear right	`VehF(1,4)`	`2`	`2`
Front left	`VehF(2,1)`	`1`	`1`	Inertial-fixed y-axis (lateral)
Front right	`VehF(2,2)`	`1`	`2`
Rear left	`VehF(2,3)`	`2`	`1`
Rear right	`VehF(2,4)`	`2`	`2`
Front left	`VehF(3,1)`	`1`	`1`	Inertial-fixed z-axis (vertical)
Front right	`VehF(3,2)`	`1`	`2`
Rear left	`VehF(3,3)`	`2`	`1`
Rear right	`VehF(3,4)`	`2`	`2`

VehM — Suspension moment on vehicle
`array`

Longitudinal, lateral, and vertical suspension moment at axle a, wheel t, applied to the vehicle at the suspension connection point, in N·m. Array dimensions are 3 by the number of wheels on the vehicle.

VehM(1,...) — Suspension moment applied to the vehicle about the inertial-fixed x-axis (longitudinal)
VehM(2,...) — Suspension moment applied to the vehicle about the inertial-fixed y-axis (lateral)
VehM(3,...) — Suspension moment applied to the vehicle about the inertial-fixed z-axis (vertical)

For example, for a two-axle vehicle with two wheels per axle, the VehM:

Signal dimensions are [3x4].

Signal contains suspension moments applied to vehicle according to the axle and wheel locations.

$VehM = M_{v} = [\begin{matrix} M_{v x_{1, 1}} & M_{v x_{1, 2}} & M_{v x_{2, 1}} & M_{v x_{2, 2}} \\ M_{v y_{1, 1}} & M_{v y_{1, 2}} & M_{v y_{2, 1}} & M_{v y_{2, 2}} \\ M_{v z_{1, 1}} & M_{v z_{1, 2}} & M_{v z_{2, 1}} & M_{v z_{2, 2}} \end{matrix}]$

Array Element	Axle	Wheel Number	Moment Axis
`VehM(1,1)`	`1`	`1`	Inertial-fixed x-axis (longitudinal)
`VehM(1,2)`	`1`	`2`
`VehM(1,3)`	`2`	`1`
`VehM(1,4)`	`2`	`2`
`VehM(2,1)`	`1`	`1`	Inertial-fixed y-axis (lateral)
`VehM(2,2)`	`1`	`2`
`VehM(2,3)`	`2`	`1`
`VehM(2,4)`	`2`	`2`
`VehM(3,1)`	`1`	`1`	Inertial-fixed z-axis (vertical)
`VehM(3,2)`	`1`	`2`
`VehM(3,3)`	`2`	`1`
`VehM(3,4)`	`2`	`2`

WhlF — Suspension force on wheel
`array`

Longitudinal, lateral, and vertical suspension forces at axle a, wheel t, applied to the wheel at the axle wheel carrier reference coordinate, in N. Array dimensions are 3 by the number of wheels on the vehicle.

WhlF(1,...) — Suspension force on wheel along the inertial-fixed x-axis (longitudinal)
WhlF(2,...) — Suspension force on wheel along the inertial-fixed y-axis (lateral)
WhlF(3,...) — Suspension force on wheel along the inertial-fixed z-axis (vertical)

For example, for a two-axle vehicle with two wheels per axle, the WhlF:

Signal dimensions are [3x4].

Signal contains wheel forces applied to the vehicle according to the axle and wheel locations.

$WhlF = F_{w} = [\begin{matrix} F_{w}_{x_{1, 1}} & F_{w}_{x_{1, 2}} & F_{w}_{x_{2, 1}} & F_{w}_{x_{2, 2}} \\ F_{w}_{y_{1, 1}} & F_{w}_{y_{1, 2}} & F_{w}_{y_{2, 1}} & F_{w}_{y_{2, 2}} \\ F_{w}_{z_{1, 1}} & F_{w}_{z_{1, 2}} & F_{w}_{z_{2, 1}} & F_{w}_{z_{2, 2}} \end{matrix}]$

Wheel	Array Element	Axle	Wheel Number	Force Axis
Front left	`WhlF(1,1)`	`1`	`1`	Inertial-fixed x-axis (longitudinal)
Front right	`WhlF(1,2)`	`1`	`2`
Rear left	`WhlF(1,3)`	`2`	`1`
Rear right	`WhlF(1,4)`	`2`	`2`
Front left	`WhlF(2,1)`	`1`	`1`	Inertial-fixed y-axis (lateral)
Front right	`WhlF(2,2)`	`1`	`2`
Rear left	`WhlF(2,3)`	`2`	`1`
Rear right	`WhlF(2,4)`	`2`	`2`
Front left	`WhlF(3,1)`	`1`	`1`	Inertial-fixed z-axis (vertical)
Front right	`WhlF(3,2)`	`1`	`2`
Rear left	`WhlF(3,3)`	`2`	`1`
Rear right	`WhlF(3,4)`	`2`	`2`

WhlV — Wheel velocity
`array`

Longitudinal, lateral, and vertical wheel velocity at axle a, wheel t, in m/s. Array dimensions are 3 by the number of wheels on the vehicle.

WhlV(1,...) — Wheel velocity along the inertial-fixed x-axis (longitudinal)
WhlV(2,...) — Wheel velocity along the inertial-fixed y-axis (lateral)
WhlV(3,...) — Wheel velocity along the inertial-fixed z-axis (vertical)

For example, for a two-axle vehicle with two wheels per axle, the WhlV:

Signal dimensions are [3x4].

Signal contains wheel forces applied to the vehicle according to the axle and wheel locations.

$WhlV = [\begin{matrix} {\dot{x}}_{w} \\ {\dot{y}}_{w} \\ {\dot{z}}_{w} \end{matrix}] = [\begin{matrix} {\dot{x}}_{w_{1, 1}} & {\dot{x}}_{w_{1, 2}} & {\dot{x}}_{w_{2, 1}} & {\dot{x}}_{w_{2, 2}} \\ {\dot{y}}_{w_{_{1, 1}}} & {\dot{y}}_{w_{1, 2}} & {\dot{y}}_{w_{2, 1}} & {\dot{y}}_{w_{2, 2}} \\ {\dot{z}}_{w_{_{1, 1}}} & {\dot{z}}_{w_{1, 2}} & {\dot{z}}_{w_{2, 1}} & {\dot{z}}_{w_{2, 2}} \end{matrix}]$

Wheel	Array Element	Axle	Wheel Number	Force Axis
Front left	`WhlV(1,1)`	`1`	`1`	Inertial-fixed x-axis (longitudinal)
Front right	`WhlV(1,2)`	`1`	`2`
Rear left	`WhlV(1,3)`	`2`	`1`
Rear right	`WhlV(1,4)`	`2`	`2`
Front left	`WhlV(2,1)`	`1`	`1`	Inertial-fixed y-axis (lateral)
Front right	`WhlV(2,2)`	`1`	`2`
Rear left	`WhlV(2,3)`	`2`	`1`
Rear right	`WhlV(2,4)`	`2`	`2`
Front left	`WhlV(3,1)`	`1`	`1`	Inertial-fixed z-axis (vertical)
Front right	`WhlV(3,2)`	`1`	`2`
Rear left	`WhlV(3,3)`	`2`	`1`
Rear right	`WhlV(3,4)`	`2`	`2`

WhlAng — Wheel camber, caster, toe angles
`array`

Camber, caster, and toe angles at axle a, wheel t, in rad. Array dimensions are 3 by the number of wheels on the vehicle.

WhlAng(1,...) — Camber angle
WhlAng(2,...) — Caster angle
WhlAng(3,...) — Toe angle

For example, for a two-axle vehicle with two wheels per axle, the WhlAng:

Signal dimensions are [3x4].

Signal contains angles according to the axle and wheel locations.

$WhlAng = [\begin{matrix} ξ \\ η \\ ζ \end{matrix}] = [\begin{matrix} ξ_{1, 1} & ξ_{1, 2} & ξ_{2, 1} & ξ_{2, 2} \\ η_{1, 1} & η_{1, 2} & η_{2, 1} & η_{2, 2} \\ ζ_{1, 1} & ζ_{1, 2} & ζ_{2, 1} & ζ_{2, 2} \end{matrix}]$

Wheel	Array Element	Axle	Wheel Number	Angle
Front left	`WhlAng(1,1)`	`1`	`1`	Camber
Front right	`WhlAng(1,2)`	`1`	`2`
Rear left	`WhlAng(1,3)`	`2`	`1`
Rear right	`WhlAng(1,4)`	`2`	`2`
Front left	`WhlAng(2,1)`	`1`	`1`	Caster
Front right	`WhlAng(2,2)`	`1`	`2`
Rear left	`WhlAng(2,3)`	`2`	`1`
Rear right	`WhlAng(2,4)`	`2`	`2`
Front left	`WhlAng(3,1)`	`1`	`1`	Toe
Front right	`WhlF(3,2)`	`1`	`2`
Rear left	`WhlF(3,3)`	`2`	`1`
Rear right	`WhlF(3,4)`	`2`	`2`

Parameters

expand all

Axles

Number of axles, NumAxl — Number of axles
`2` (default) | `scalar`

Number of axles, N_a, dimensionless.

Number of wheels by axle, NumWhlsByAxl — Number of wheels per axle
`[2 2]` (default) | `vector`

Number of wheels per axle, Nt_a, dimensionless. Vector is 1 by the number of vehicle axles, N_a. For example, [1,2] represents one wheel on axle one and two wheels on axle two.

Steered axle enable by axle, StrgEnByAxl — Boolean vector to enable axle steering
`[1 0]` (default) | `vector`

Boolean vector that enables axle steering, En_steer, dimensionless. Vector is 1 by the number of vehicle axles, N_a. For example:

[1 0]—For a two-axle vehicle, enables axle one steering and disables axle two steering
[1 1]—For a two-axle vehicle, enables axle one and axle two steering

Dependencies

Setting an element of the Steered axle enable by axle, StrgEnByAxl vector to 1:

Creates input port StrgAng.
Creates these parameters
- Toe angle vs steering angle slope, ToeStrgSlp
- Caster angle vs steering angle slope, CasterStrgSlp
- Camber angle vs steering angle slope, CamberStrgSlp
- Suspension height vs steering angle slope, StrgHgtSlp

For example, for a two-axle vehicle with two wheels per axle, you can input steering angles for both wheels on the first axle.

To enable the StrgAng port, set Steered axle enable by axle, StrgEnByAxl to [1 0]. The input signal array dimensions are [1x2].
The StrgAng signal contains two steering angles according to their axle and wheel locations.
$StrgAng = δ_{s t e e r} = [\begin{matrix} δ_{s t e e r_{1, 1}} & δ_{s t e e r_{1, 2}} \end{matrix}]$
Wheel Array Element Axle Wheel Number
Front left StrgAng(1,1) 1 1
Front right StrgAng(1,2) 1 2

Wheel	Array Element	Axle	Wheel Number
Front left	`StrgAng(1,1)`	`1`	`1`
Front right	`StrgAng(1,2)`	`1`	`2`

Axle and wheels lumped principal moments of inertia about longitudinal axis, AxlIxx — Inertia
`300` (default) | `vector`

Axle and wheels lumped principal moments of inertia about longitudinal axis, AxleIxx a, in kg*m^2.

Vector is 1 by the number of vehicle axles, N_a. If you provide a scalar value, the block uses that value for all axles.

Axle and wheels lumped mass, AxlM — Mass
`[2 2]` (default) | `vector`

Axle and wheels lumped mass, a, in kg.

Vector is 1 by the number of vehicle axles, N_a. If you provide a scalar value, the block uses that value for all axles.

Track hardpoint coordinates relative to axle center, TrackCoords — Point
`[0 0 0 0;-1 1 -1 1;0 0 0 0]` (default) | `array`

Track hardpoint coordinates, Tc_t, along the solid axle x, y, and z-axes, in m.

For example, for a two-axle vehicle with two wheels per axle, the TrackCoords array:

Dimensions are [3x4].

Contains four track hardpoint coordinates according to their axle and wheel locations.

$T c_{t} = [\begin{matrix} x_{w_{1, 1}} & x_{w_{1, 2}} & x_{w_{2, 1}} & x_{w_{2, 2}} \\ y_{w_{1, 1}} & y_{w_{1, 2}} & y_{w_{2, 1}} & y_{w_{2, 2}} \\ z_{w_{1, 1}} & z_{w_{1, 2}} & z_{w_{2, 1}} & z_{w_{2, 2}} \end{matrix}]$

Array Element	Axle	Wheel Number	Axis
`TrackCoords(1,1)`	`1`	`1`	Solid axle x-axis
`TrackCoords(1,2)`	`1`	`2`
`TrackCoords(1,3)`	`2`	`1`
`TrackCoords(1,4)`	`2`	`2`
`TrackCoords(2,1)`	`1`	`1`	Solid axle y-axis
`TrackCoords(2,2)`	`1`	`2`
`TrackCoords(2,3)`	`2`	`1`
`TrackCoords(2,4)`	`2`	`2`
`TrackCoords(3,1)`	`1`	`1`	Solid axle z-axis
`TrackCoords(3,2)`	`1`	`2`
`TrackCoords(3,3)`	`2`	`1`
`TrackCoords(3,4)`	`2`	`2`

Suspension hardpoint coordinates relative to axle center, SuspCoords — Point
`[0 0 0 0;-1 1 -1 1;0 0 0 0]` (default) | `array`

Suspension hardpoint coordinates, Sc_t, along the solid axle x-, y-, and z-axes, in m.

For example, for a two-axle vehicle with two wheels per axle, the SuspCoords array:

Dimensions are [3x4].

Contains four track hardpoint coordinates according to their axle and track locations.

$S c_{t} = [\begin{matrix} x_{s_{1, 1}} & x_{s_{1, 2}} & x_{s_{2, 1}} & x_{s_{2, 2}} \\ y_{s_{1, 1}} & y_{s_{1, 2}} & y_{s_{2, 1}} & y_{s_{2, 2}} \\ z_{s_{1, 1}} & z_{s_{1, 2}} & z_{s_{2, 1}} & z_{s_{2, 2}} \end{matrix}]$

Array Element	Axle	Track	Axis
`SuspCoords(1,1)`	`1`	`1`	Solid axle x-axis
`SuspCoords(1,2)`	`1`	`2`
`SuspCoords(1,3)`	`2`	`1`
`SuspCoords(1,4)`	`2`	`2`
`SuspCoords(2,1)`	`1`	`1`	Solid axle y-axis
`SuspCoords(2,2)`	`1`	`2`
`SuspCoords(2,3)`	`2`	`1`
`SuspCoords(2,4)`	`2`	`2`
`SuspCoords(3,1)`	`1`	`1`	Solid axle z-axis
`SuspCoords(3,2)`	`1`	`2`
`SuspCoords(3,3)`	`2`	`1`
`SuspCoords(3,4)`	`2`	`2`

Wheel and axle interface compliance constant, KzWhlAxl — Spring rate
`6437000` (default) | `scalar`

Wheel and axle interface compliance constant, kwa_z, in N/m.

Wheel and axle interface compliance preload, F0zWhlAxl — Spring rate
`9810` (default) | `scalar`

Wheel and axle interface compliance preload, Fwa_z0, in N.

Wheel and axle interface damping constant, CzWhlAxl — Damping
`10000` (default) | `scalar`

Wheel and axle interface damping constant, cwa_z, in m.

Suspension

Compliance and Damping - Passive

Suspension spring constant, Kz — Suspension spring constant
`64370` (default) | `scalar` | `vector`

Linear vertical spring constant for independent suspension wheels on axle a, k_{z_a}, in N/m.

Vector is 1 by the number of vehicle axles, N_a. If you provide a scalar value, the block uses that value for all axles.

Suspension spring preload, F0z — Suspension spring preload
`9810` (default) | `scalar` | `vector`

Vertical preload spring force applied to the wheels on the axle at wheel carrier reference coordinates, F_{z0_a}, in N. Positive preload forces:

Cause the vehicle to lift.
Point along the negative inertial-fixed z-axis.

Vector is 1 by the number of vehicle axles, N_a. If you provide a scalar value, the block uses that value for all axles.

Suspension shock damping constant, Cz — Suspension shock damping constant
`10000` (default) | `scalar` | `vector`

Linear vertical damping constant for independent suspension wheels on axle a, c_{z_a}, in Ns/m.

Vector is 1 by the number of vehicle axles, N_a. If you provide a scalar value, the block uses that value for all axles.

Dependencies

To create this parameter, clear Enable active damping.

Suspension maximum height, Hmax — Height
`0.5` (default) | `scalar` | `vector`

Maximum suspension extension or minimum suspension compression height, H_max, for axle a before the suspension reaches a hardstop, in m.

Vector is 1 by the number of vehicle axles, N_a. If you provide a scalar value, the block uses that value for all axles.

Geometry

Toe angle at steering center, Toe — Toe angle
`0.0349` (default) | `scalar`

Nominal suspension toe angle at zero steering angle, ζ_0a, in rad.

Roll steer vs suspension height slope, RollStrgSlp — Steer angle suspension slope
`-0.2269` (default) | `scalar` | `vector`

Roll steer angle versus suspension height, m_{htoe_a}, in rad/m.

Vector is 1 by the number of vehicle axles, N_a. If you provide a scalar value, the block uses that value for all axles.

Toe angle vs steering angle slope, ToeStrgSlp — Toe angle steering slope
`0.01` (default) | `scalar` | `vector`

Toe angle versus steering angle slope, m_{toesteer_a}, dimensionless.

Vector is 1 by the number of vehicle axles, N_a. If you provide a scalar value, the block uses that value for all axles.

Dependencies

To enable the port StrgAng, set an element of the Steered axle enable by axle, StrgEnByAxl vector to 1.

Caster angle at steering center, Caster — Caster angle at steering center
`0.0698` (default) | `scalar`

Nominal suspension caster angle at zero steering angle, η_0a, in rad.

Caster angle vs suspension height slope, CasterHslp — Caster angle versus suspension height slope
`-0.2269` (default) | `scalar` | `vector`

Caster angle versus suspension height, m_{hcaster_a}, in rad/m.

Vector is 1 by the number of vehicle axles, N_a. If you provide a scalar value, the block uses that value for all axles.

Caster angle vs steering angle slope, CasterStrgSlp — Caster angle versus steering angle slope
`0.01` (default) | `scalar` | `vector`

Caster angle versus steering angle slope, m_{castersteer_a}, dimensionless.

Vector is 1 by the number of vehicle axles, N_a. If you provide a scalar value, the block uses that value for all axles.

Dependencies

To enable the port StrgAng, set an element of the Steered axle enable by axle, StrgEnByAxl vector to 1.

Camber angle at steering center, Camber — Camber angle at steering center
`0.0698` (default) | `scalar`

Nominal suspension camber angle at zero steering angle, ξ_0a, in rad.

Camber angle vs suspension height slope, CamberHslp — Camber angle versus suspension height slope
`-0.2269` (default) | `scalar` | `vector`

Camber angle versus suspension height, m_{hcamber_a}, in rad/m.

Vector is 1 by the number of vehicle axles, N_a. If you provide a scalar value, the block uses that value for all axles.

Camber angle vs steering angle slope, CamberStrgSlp — Camber angle versus steering angle slope
`0.01` (default) | `scalar` | `vector`

Camber angle versus steering angle slope, m_{cambersteer_a}, dimensionless.

Vector is 1 by the number of vehicle axles, N_a. If you provide a scalar value, the block uses that value for all axles.

Dependencies

To enable the port StrgAng, set an element of the Steered axle enable by axle, StrgEnByAxl vector to 1.

Suspension height vs steering angle slope, StrgHgtSlp — Suspension height versus steering angle slope
`0.1432` (default) | `scalar` | `vector`

Steering angle to vertical force slope applied at suspension wheel carrier reference point, m_{hsteer_a}, in m/rad.

Vector is 1 by the number of vehicle axles, N_a. If you provide a scalar value, the block uses that value for all axles.

Dependencies

To enable the port StrgAng, set an element of the Steered axle enable by axle, StrgEnByAxl vector to 1.

References

[1] Gillespie, Thomas. Fundamentals of Vehicle Dynamics. Warrendale, PA: Society of Automotive Engineers, 1992.

[2] Vehicle Dynamics Standards Committee. Vehicle Dynamics Terminology. SAE J670. Warrendale, PA: Society of Automotive Engineers, 2008.

[3] Technical Committee. Road vehicles — Vehicle dynamics and road-holding ability — Vocabulary. ISO 8855:2011. Geneva, Switzerland: International Organization for Standardization, 2011.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced in R2018a

expand all

R2022b: Parameter name change from `NumTracksByAxl` to `NumWhlsByAxl`

The Number of tracks by axle, NumTracksByAxl parameter is renamed to Number of wheels by axle, NumWhlsByAxl.

The block uses the number of wheels per axle to index the input and output block signals.

Solid Axle Suspension - Leaf Spring

Description

Suspension Compliance and Damping

Hardstop Forces

Camber, Caster, and Toe Angles

Steering Angles

Power and Energy

Examples

Kinematics and Compliance Virtual Test Laboratory Reference Application

Ports

Input

WhlPz — Wheel z-axis displacement array

WhlRe — Wheel effective radius array

WhlVz — Wheel z-axis velocity array

WhlFx — Longitudinal wheel force on vehicle array

WhlFy — Lateral wheel force on vehicle array

WhlM — Suspension moment on wheel array

VehP — Vehicle displacement array

VehV — Vehicle velocity array

StrgAng — Steering angle, optional array

Dependencies

Output

Info — Bus signal bus

VehF — Suspension force on vehicle array

VehM — Suspension moment on vehicle array

WhlF — Suspension force on wheel array

WhlV — Wheel velocity array

WhlAng — Wheel camber, caster, toe angles array

Parameters

Axles

Number of axles, NumAxl — Number of axles 2 (default) | scalar

Number of wheels by axle, NumWhlsByAxl — Number of wheels per axle [2 2] (default) | vector

Steered axle enable by axle, StrgEnByAxl — Boolean vector to enable axle steering [1 0] (default) | vector

Dependencies

Axle and wheels lumped principal moments of inertia about longitudinal axis, AxlIxx — Inertia 300 (default) | vector

Axle and wheels lumped mass, AxlM — Mass [2 2] (default) | vector

Track hardpoint coordinates relative to axle center, TrackCoords — Point [0 0 0 0;-1 1 -1 1;0 0 0 0] (default) | array

Suspension hardpoint coordinates relative to axle center, SuspCoords — Point [0 0 0 0;-1 1 -1 1;0 0 0 0] (default) | array

Wheel and axle interface compliance constant, KzWhlAxl — Spring rate 6437000 (default) | scalar

Wheel and axle interface compliance preload, F0zWhlAxl — Spring rate 9810 (default) | scalar

Wheel and axle interface damping constant, CzWhlAxl — Damping 10000 (default) | scalar

Suspension

Suspension spring constant, Kz — Suspension spring constant 64370 (default) | scalar | vector

Suspension spring preload, F0z — Suspension spring preload 9810 (default) | scalar | vector

Suspension shock damping constant, Cz — Suspension shock damping constant 10000 (default) | scalar | vector

Dependencies

Suspension maximum height, Hmax — Height 0.5 (default) | scalar | vector

Toe angle at steering center, Toe — Toe angle 0.0349 (default) | scalar

Roll steer vs suspension height slope, RollStrgSlp — Steer angle suspension slope -0.2269 (default) | scalar | vector

Toe angle vs steering angle slope, ToeStrgSlp — Toe angle steering slope 0.01 (default) | scalar | vector

Dependencies

Caster angle at steering center, Caster — Caster angle at steering center 0.0698 (default) | scalar

Caster angle vs suspension height slope, CasterHslp — Caster angle versus suspension height slope -0.2269 (default) | scalar | vector

Caster angle vs steering angle slope, CasterStrgSlp — Caster angle versus steering angle slope 0.01 (default) | scalar | vector

Dependencies

Camber angle at steering center, Camber — Camber angle at steering center 0.0698 (default) | scalar

Camber angle vs suspension height slope, CamberHslp — Camber angle versus suspension height slope -0.2269 (default) | scalar | vector

Camber angle vs steering angle slope, CamberStrgSlp — Camber angle versus steering angle slope 0.01 (default) | scalar | vector

Dependencies

Suspension height vs steering angle slope, StrgHgtSlp — Suspension height versus steering angle slope 0.1432 (default) | scalar | vector

Dependencies

References

Extended Capabilities

C/C++ Code Generation Generate C and C++ code using Simulink® Coder™.

Version History

R2022b: Parameter name change from NumTracksByAxl to NumWhlsByAxl

See Also

WhlPz — Wheel `z`-axis displacement
array

WhlRe — Wheel effective radius
array

WhlVz — Wheel `z`-axis velocity
array

WhlFx — Longitudinal wheel force on vehicle
array

WhlFy — Lateral wheel force on vehicle
array

WhlM — Suspension moment on wheel
array

VehP — Vehicle displacement
array

VehV — Vehicle velocity
array

StrgAng — Steering angle, optional
array

Info — Bus signal
bus

VehF — Suspension force on vehicle
`array`

VehM — Suspension moment on vehicle
`array`

WhlF — Suspension force on wheel
`array`

WhlV — Wheel velocity
`array`

WhlAng — Wheel camber, caster, toe angles
`array`

Number of axles, NumAxl — Number of axles
`2` (default) | `scalar`

Number of wheels by axle, NumWhlsByAxl — Number of wheels per axle
`[2 2]` (default) | `vector`

Steered axle enable by axle, StrgEnByAxl — Boolean vector to enable axle steering
`[1 0]` (default) | `vector`

Axle and wheels lumped principal moments of inertia about longitudinal axis, AxlIxx — Inertia
`300` (default) | `vector`

Axle and wheels lumped mass, AxlM — Mass
`[2 2]` (default) | `vector`

Track hardpoint coordinates relative to axle center, TrackCoords — Point
`[0 0 0 0;-1 1 -1 1;0 0 0 0]` (default) | `array`

Suspension hardpoint coordinates relative to axle center, SuspCoords — Point
`[0 0 0 0;-1 1 -1 1;0 0 0 0]` (default) | `array`

Wheel and axle interface compliance constant, KzWhlAxl — Spring rate
`6437000` (default) | `scalar`

Wheel and axle interface compliance preload, F0zWhlAxl — Spring rate
`9810` (default) | `scalar`

Wheel and axle interface damping constant, CzWhlAxl — Damping
`10000` (default) | `scalar`

Suspension spring constant, Kz — Suspension spring constant
`64370` (default) | `scalar` | `vector`

Suspension spring preload, F0z — Suspension spring preload
`9810` (default) | `scalar` | `vector`

Suspension shock damping constant, Cz — Suspension shock damping constant
`10000` (default) | `scalar` | `vector`

Suspension maximum height, Hmax — Height
`0.5` (default) | `scalar` | `vector`

Toe angle at steering center, Toe — Toe angle
`0.0349` (default) | `scalar`

Roll steer vs suspension height slope, RollStrgSlp — Steer angle suspension slope
`-0.2269` (default) | `scalar` | `vector`

Toe angle vs steering angle slope, ToeStrgSlp — Toe angle steering slope
`0.01` (default) | `scalar` | `vector`

Caster angle at steering center, Caster — Caster angle at steering center
`0.0698` (default) | `scalar`

Caster angle vs suspension height slope, CasterHslp — Caster angle versus suspension height slope
`-0.2269` (default) | `scalar` | `vector`

Caster angle vs steering angle slope, CasterStrgSlp — Caster angle versus steering angle slope
`0.01` (default) | `scalar` | `vector`

Camber angle at steering center, Camber — Camber angle at steering center
`0.0698` (default) | `scalar`

Camber angle vs suspension height slope, CamberHslp — Camber angle versus suspension height slope
`-0.2269` (default) | `scalar` | `vector`

Camber angle vs steering angle slope, CamberStrgSlp — Camber angle versus steering angle slope
`0.01` (default) | `scalar` | `vector`

Suspension height vs steering angle slope, StrgHgtSlp — Suspension height versus steering angle slope
`0.1432` (default) | `scalar` | `vector`

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

R2022b: Parameter name change from `NumTracksByAxl` to `NumWhlsByAxl`