Main Content

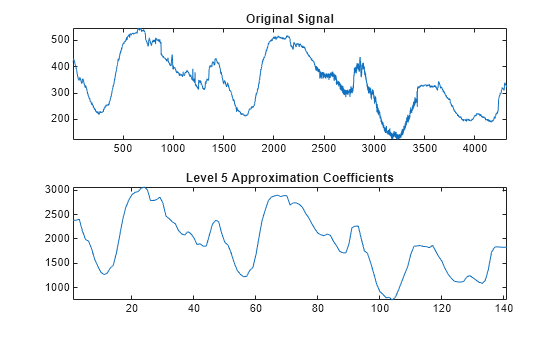
appcoef

1-D approximation coefficients

collapse all in page

Syntax

A = appcoef(c,l,wname)
A = appcoef(c,l,LoR,HiR)
A = appcoef(___,N)
A = appcoef(___,Mode=extmode)

Description

A = appcoef(c,l,wname) returns the approximation coefficients at the coarsest scale using the wavelet decomposition structure [c,l] of a 1-D signal and the wavelet specified by wname. For more information, see wavedec.

A = appcoef(c,l,LoR,HiR) uses the lowpass reconstruction filter LoR and highpass reconstruction filter HiR.

A = appcoef(___,N) returns the approximation coefficients at level N. If [c,l] is the M-level wavelet decomposition structure of a 1-D signal, then 0 ≤ N ≤ M = length(l)-2.

example

A = appcoef(___,Mode=extmode) uses the specified discrete wavelet transform (DWT) extension mode extmode. This syntax can be used with either of the previous syntaxes.

Examples

collapse all

Open Live Script

Load the signal consisting of electricity usage data.

load leleccum

Obtain the DWT down to level 5 using the sym4 wavelet.

[c,l] = wavedec(leleccum,5,"sym4");

Extract the approximation coefficients at the coarsest scale. Plot the original signal and the approximation coefficients.

lev = 5;
a3 = appcoef(c,l,"sym4",lev);
tiledlayout(2,1)
nexttile
plot(leleccum)
axis tight
title("Original Signal")
nexttile
plot(a3)
axis tight
title("Level "+num2str(lev)+" Approximation Coefficients")

Figure contains 2 axes objects. Axes object 1 with title Original Signal contains an object of type line. Axes object 2 with title Level 5 Approximation Coefficients contains an object of type line.

Input Arguments

collapse all

Wavelet decomposition vector of a 1-D signal, specified as a vector. For more information, see wavedec.

Example: [c,l] = wavedec(randn(1,256),4,"coif1") returns the wavelet decomposition of a vector down to level 4.

Data Types: single | double
Complex Number Support: Yes

Bookkeeping vector of the wavelet decomposition of a 1-D signal, specified as a vector of positive integers. The bookkeeping vector is used to parse the coefficients in the wavelet decomposition vector c by level. For more information, see wavedec.

Data Types: single | double

Wavelet used to generate the wavelet decomposition [c,l], specified as a character vector or string scalar. The wavelet is from one of the following wavelet families: Best-localized Daubechies, Beylkin, Coiflets, Daubechies, Fejér-Korovkin, Haar, Han linear-phase moments, Morris minimum-bandwidth, Symlets, Vaidyanathan, Discrete Meyer, Biorthogonal, and Reverse Biorthogonal. See wavemngr for the wavelets available in each family.

Example: "db4"

Wavelet reconstruction filters, specified as a pair of even-length real-valued vectors. LoR is the lowpass reconstruction filter, and HiR is the highpass reconstruction filter. The lengths of LoR and HiR must be equal. For perfect reconstruction, LoR and HiR must be the reconstruction filters associated with the same wavelet used to obtain the wavelet decomposition c and l. For more information, see wfilters

Data Types: single | double

Approximation coefficients level, specified as a positive integer. If [c,l] is the M-level wavelet decomposition structure of a 1-D signal, then 0 ≤ N ≤ M.

Since R2023b

Extension mode to use for the inverse DWT, specified as:

mode

DWT Extension Mode

"zpd"

Zero extension

"sp0"

Smooth extension of order 0

"spd" (or "sp1")

Smooth extension of order 1

"sym" or "symh"

Symmetric extension (half point): boundary value symmetric replication

"symw"

Symmetric extension (whole point): boundary value symmetric replication

"asym" or "asymh"

Antisymmetric extension (half point): boundary value antisymmetric replication

"asymw"

Antisymmetric extension (whole point): boundary value antisymmetric replication

"ppd", "per"

Periodized extension

If the signal length is odd and mode is "per", an extra sample equal to the last value is added to the right and the extension is performed in "ppd" mode. If the signal length is even, "per" is equivalent to "ppd".

The global variable managed by dwtmode specifies the default extension mode. For perfect reconstruction, use the same extension mode that was used to obtain c and l from wavedec.

Output Arguments

collapse all

Approximation coefficients at level N, returned as a vector.

Algorithms

The input vectors c and l contain all the information about the signal decomposition.

Let NMAX = length(l)-2; then c = [A(NMAX) D(NMAX) ... D(1)] where A and the D are vectors. If N = NMAX, then a simple extraction is done; otherwise, appcoef computes iteratively the approximation coefficients using the inverse wavelet transform.

Extended Capabilities

Version History

Introduced before R2006a

expand all

See Also

|