cmddenoise
Interval-dependent denoising
Syntax
Description
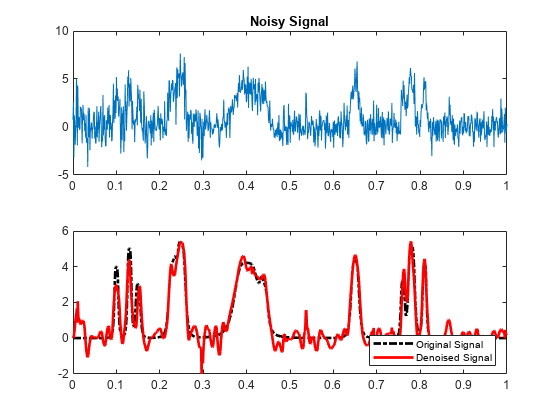
sigden = cmddenoise(sig,wname,level)sigden, obtained from an
interval-dependent denoising of the signal, sig, using the
orthogonal or biorthogonal wavelet and scaling filters,
wname. cmddenoise thresholds the
wavelet (detail) coefficients down to level, level, and
reconstructs a signal approximation using the modified detail coefficients.
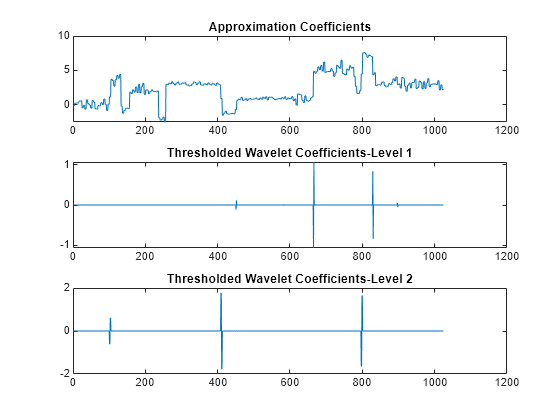
cmddenoise partitions the signal into intervals based
on variance change points in the first level detail coefficients and thresholds
each interval separately. The location and number of variance change points are
automatically selected using a penalized contrast function [2]. The minimum delay between change points is 10 samples. Thresholds are
obtained using a minimax threshold rule and soft thresholding is used to modify
the wavelet coefficients [1].
sigden = cmddenoise(sig,wname,level,sorh,nb_inter,thrParamsIn)sigden, with the denoising
intervals and corresponding thresholds specified as a cell array of
matrices with length equal to level. Each element
of the cell array contains the interval and threshold information
for the corresponding level of the wavelet transform. The elements
of thrParamsIn are N-by-3 matrices with N equal
to the number of intervals. The 1st and 2nd columns contain the beginning
and ending indices of the intervals and the 3rd column contains the
corresponding threshold value. If you specify thrParamsIn, cmddenoise ignores
the value of nb_inter.
[ returns a cell array, sigden,coefs,thrParamsOut]
= cmddenoise(___)thrParamsOut,
with length equal to level. Each element of thrParamsOut is
an N-by-3 matrix. The row dimension of the matrix elements is the
number of intervals and is determined by the value of the input arguments.
Each row of the matrix contains the beginning and end points (indices)
of the thresholded interval and the corresponding threshold value.
[ returns
a cell array, sigden,coefs,thrParamsOut,int_DepThr_Cell]
= cmddenoise(sig,wname,level,sorh,nb_inter)int_DepThr_Cell, with length equal
to 6. int_DepThr_Cell contains interval and threshold
information assuming the number of change points ranges from 0 to
5. The N-th element of int_DepThr_Cell is a N-by-3
matrix containing the interval information assuming N-1 change points.
Each row of the matrix contains the beginning and end points (indices)
of the thresholded interval and the corresponding threshold value.
Attempting to output int_DepThr_Cell if you use
the input argument, thrParamsIn, results in an
error.
[ returns
the optimal number of signal intervals based on the estimated variance
change points in the level-1 detail coefficients. To estimate the
number of change points, sigden,coefs,thrParamsOut,int_DepThr_Cell,BestNbofInt]
= cmddenoise(sig,wname,level,sorh,nb_inter)cmddenoise assumes the
total number is less than or equal to 6 and uses a penalized contrast [2].
Attempting to output BestNbofInt if you use the
input argument, thrParamsIn, results in an error.
Examples
Denoising Blocks Signal with Haar Wavelet
Load the noisy blocks signal, nblocr1.mat. The signal consists of a piecewise constant signal in additive white Gaussian noise. The variance of the additive noise differs in three disjoint intervals.
load nblocr1;Apply interval-dependent denoising down to level 4 using the Haar wavelet. |cmddenoise automatically determines the optimal number and locations of the variance change points. Plot the denoised and original signal for comparison.
sigden = cmddenoise(nblocr1,'db1',4); plot(nblocr1); hold on; plot(sigden,'r','linewidth',2); axis tight;
Denoising Blocks Signal with Hard Thresholding
Load the noisy blocks signal, nblocr1.mat. The signal consists of a piecewise constant signal in additive white Gaussian noise. The variance of the additive noise differs in three disjoint intervals.
load nblocr1;Apply interval-dependent denoising down to level 4 using the Haar wavelet and a hard thresholding rule. cmddenoise automatically determines the optimal number and locations of the intervals. Plot the original and denoised signals.
sorh = 'h'; sigden = cmddenoise(nblocr1,'db1',4,sorh); plot(nblocr1); hold on; plot(sigden,'r','linewidth',2); axis tight; legend('Original Signal','Denoised Signal','Location','NorthWest');
Specify the Number of Intervals
Create a signal sampled at 1 kHz. The signal consists of a series of bumps of various widths.
t = [0.1 0.13 0.15 0.23 0.25 0.40 0.44 0.65 0.76 0.78 0.81]; h = [4 -5 3 -4 5 -4.2 2.1 4.3 -3.1 5.1 -4.2]; h = abs(h); len = 1000; w = 0.01*[0.5 0.5 0.6 1 1 3 1 1 0.5 0.8 0.5]; tt = linspace(0,1,len); x = zeros(1,len); for j=1:11 x = x + ( h(j) ./ (1+ ((tt-t(j))/w(j)).^4)); end
Add white Gaussian noise with different variances to two disjoint segments of the signal. Add zero-mean white Gaussian noise with variance equal to 2 to the signal segment from 0 to 0.3 seconds. Add zero-mean white Gaussian noise with unit variance to the signal segment from 0.3 seconds to 1 second. Set the random number generator to the default settings for reproducible results.
rng default; nv1 = sqrt(2).*randn(size(tt)).*(tt<=0.3); nv2 = randn(size(tt)).*(tt>0.3); xx = x+nv1+nv2; sigden = cmddenoise(xx,'sym5',5,'s',2);
Apply interval-dependent denoising using the Daubechies' least-asymmetric wavelet with 5 vanishing moments down to level 3. Set the number of intervals to 2. Plot the noisy signal, original signal, and denoised signal for comparison.
sigden = cmddenoise(xx,'sym5',3,'s',2); subplot(211) plot(tt,xx); title('Noisy Signal'); subplot(212) plot(tt,x,'k-.','linewidth',2); hold on; plot(tt,sigden,'r','linewidth',2); legend('Original Signal','Denoised Signal','Location','SouthEast');
Specify Intervals and Thresholds
Load the example signal nbumpr1.mat. The variance of the additive noise differs in three disjoint intervals.
load nbumpr1.mat;Use a level-5 multiresolution analysis. Create a cell array of length 5 consisting of 3-by-3 matrices. The first two elements of each row contain the beginning and ending indices of the interval and the last element of each row is the corresponding threshold.
wname = 'sym4'; level = 5; sorh = 's'; thrParamsIn = {... [... 1 207 1.0482; ... 207 613 2.5110; ... 613 1024 1.0031; ... ]; ... [... 1 207 1.04824; ... 207 613 3.8718; ... 613 1024 1.04824; ... ]; ... [... 1 207 1.04824; ... 207 613 1.99710; ... 613 1024 1.65613; ... ]; ... [... 1 207 1.04824; ... 207 613 2.09117; ... 613 1024 1.04824; ... ]; ... [... 1 207 1.04824; ... 207 613 1.78620; ... 613 102 1.04824; ... ]; ... };
Denoise the signal using the threshold settings and the Daubechies' least-asymmetric wavelet with 4 vanishing moments. Use a soft thresholding rule. Plot the noisy and denoised signals for comparison.
wname = 'sym4'; level = 5; sorh = 's'; sigden = cmddenoise(nbumpr1,wname,level,sorh,... NaN,thrParamsIn); plot(nbumpr1); hold on; plot(sigden,'r','linewidth',2); axis tight; legend('Noisy Signal','Denoised Signal','Location','NorthEast');
Return Denoised Wavelet Coefficients
Load the example signal nblocr1.mat. Use the Haar wavelet and decompose the signal down to level 2. Obtain the discrete wavelet transform and denoise the signal. Return the wavelet coefficients of the noisy and denoised signals.
load nblocr1.mat; [sigden,coefs] = cmddenoise(nblocr1,'db1',2); [C,L] = wavedec(nblocr1,2,'db1');
Plot reconstructions based on the level-2 approximation and level-2 and level-1 detail coefficients for the noisy signal.
app = wrcoef('a',C,L,'db1',2); subplot(3,1,1); plot(app); title('Approximation Coefficients'); for nn = 1:2 det = wrcoef('d',C,L,'db1',nn); subplot(3,1,nn+1) plot(det); title(['Noisy Wavelet Coefficients - Level '... num2str(nn)]); end
Plot reconstructions based on the approximation and detail coefficients for the denoised signal at the same levels.
figure; app = wrcoef('a',coefs,L,'db1',2); subplot(3,1,1); plot(app); title('Approximation Coefficients'); for nn = 1:2 det = wrcoef('d',coefs,L,'db1',nn); subplot(3,1,nn+1) plot(det); title(['Thresholded Wavelet Coefficients-Level '... num2str(nn)]); end
The approximation coefficients are identical in the noisy and denoised signal, but most of the detail coefficients in the denoised signal are close to zero.
Output Intervals and Thresholds
Create a signal sampled at 1 kHz. The signal consists of a series of bumps of various widths.
t = [0.1 0.13 0.15 0.23 0.25 0.40 0.44 0.65 0.76 0.78 0.81]; h = [4 -5 3 -4 5 -4.2 2.1 4.3 -3.1 5.1 -4.2]; h = abs(h); len = 1000; w = 0.01*[0.5 0.5 0.6 1 1 3 1 1 0.5 0.8 0.5]; tt = linspace(0,1,len); x = zeros(1,len); for j=1:11 x = x + ( h(j) ./ (1+ ((tt-t(j))/w(j)).^4)); end plot(tt,x); title('Original Signal'); hold on;
Add white Gaussian noise with different variances to two disjoint segments of the signal. Add zero-mean white Gaussian noise with variance equal to 2 to the signal segment from 0 to 0.3 seconds. Add zero-mean white Gaussian noise with unit variance to the signal segment from 0.3 seconds to 1 second. Set the random number generator to the default settings for reproducible results.
rng default; nv1 = sqrt(2).*randn(size(tt)).*(tt<=0.3); nv2 = randn(size(tt)).*(tt>0.3); xx = x+nv1+nv2; plot(tt,xx); title('Noisy Signal');
Apply interval-dependent denoising using the Daubechies' least- asymmetric wavelet with 4 vanishing moments down to level 5. Automatically choose the number of intervals and output the result.
[sigden,coefs,thrParamsOut] = cmddenoise(xx,'sym4',5);
thrParamsOut{1}ans = 2×3
103 ×
0.0010 0.2930 0.0036
0.2930 1.0000 0.0028
cmdnoise identifies one variance change point in the 1st level detail coefficients defining two intervals. The first interval contains samples 1 to 293. The second interval contains samples 293 to 1000. This is close to the true variance change point, which occurs at sample 299.
Partition Signal into Increasing Numbers of Intervals with Thresholds
Load the example signal, nbumpr1.mat. Partition the signal into 1 to 6 intervals assuming 0 to 5 change points. Compute the thresholds for each interval. Using the Daubechies' least-asymmetric wavelet with 4 vanishing moments return the intervals and corresponding thresholds. Display the results.
load nbumpr1.mat; [sigden,~,~,int_DepThr_Cell] = cmddenoise(nbumpr1,'sym4',1); format bank; disp(' Begin End Threshold ');
Begin End Threshold
cellfun(@disp,int_DepThr_Cell,'UniformOutput',false); 1.00 1024.00 1.36
1.00 613.00 1.73
613.00 1024.00 1.00
1.00 207.00 1.05
207.00 613.00 2.51
613.00 1024.00 1.00
1.00 207.00 1.05
207.00 597.00 2.52
597.00 627.00 1.69
627.00 1024.00 0.97
1.00 207.00 1.05
207.00 613.00 2.51
613.00 695.00 1.20
695.00 725.00 0.59
725.00 1024.00 1.05
1.00 207.00 1.05
207.00 597.00 2.52
597.00 627.00 1.69
627.00 695.00 1.19
695.00 725.00 0.59
725.00 1024.00 1.05
Detect Number of Change Points
Load the example signal, nbumpr1.mat. The signal has two variance change points, which results in three intervals. Use cmddenoise to detect the number of change points.
load nbumpr1.mat; [sigden,~,thrParamsOut,~,bestNbofInt] = ... cmddenoise(nbumpr1,'sym4',1); fprintf('Found %d change points.\n',bestNbofInt-1);
Found 2 change points.
Input Arguments
Output Arguments
References
[1] Donoho, D. and Johnstone, I. “Ideal spatial adaptation by wavelet shrinkage”, Biometrika, 1994, 81,3, 425–455.
[2] Lavielle, M. “Detection of multiple changes in a sequence of dependent variables”, Stochastic Processes and their Applications, 1999, 83, 79–102.
Version History
Introduced in R2010a
You can also select a web site from the following list
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)
Asia Pacific
- Australia (English)
- India (English)
- New Zealand (English)
- 中国
- 日本Japanese (日本語)
- 한국Korean (한국어)