lwt2
Description
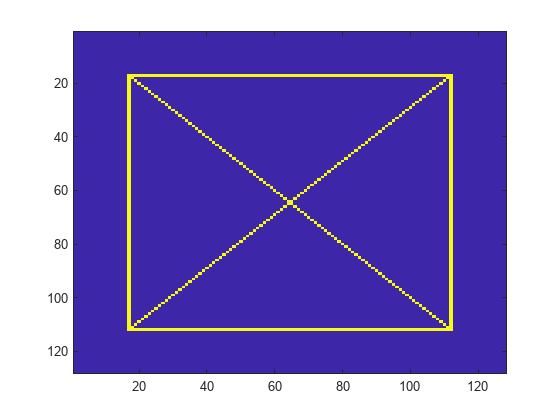
[
performs the 2-D lifting wavelet transform (LWT) of the real- or complex-valued
matrix ll,lh,hl,hh] = lwt2(x)x using the db1 wavelet. The function
performs the decomposition first along the rows in x and then
along the columns. The default decomposition level depends on the size of
x. For more information, see Level. The function returns the approximation coefficients at the
coarsest scale and the horizontal, vertical, and diagonal detail coefficients by
level.
If x is a single-precision input, the numeric type of the
coefficients is single precision. Otherwise, the numeric type is double
precision.
[___] = lwt2(
specifies options using one or more name-value arguments. For example,
x,Name=Value)lwt2(x,Wavelet="db2",Level=3) performs 2-D LWT using the
db2 wavelet and a level 3 decomposition.
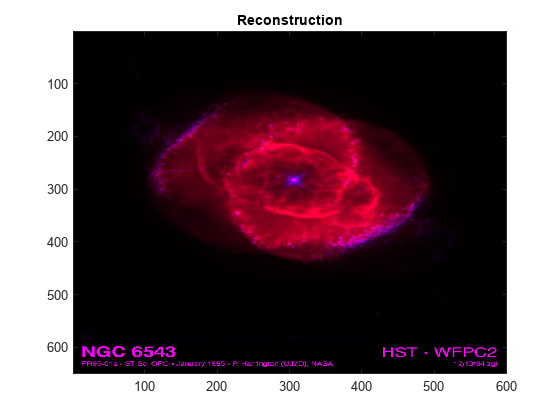
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Algorithms
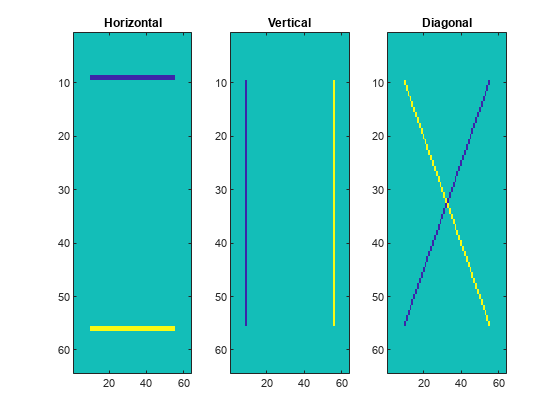
At each stage of a 2-D wavelet decomposition, the approximation coefficients at level j are decomposed into four components: the approximation at level j+1 and the details in three orientations (horizontal, vertical, and diagonal). Each component is the result of convolving the rows and columns of the level j approximation with the appropriate combination of lowpass and highpass filters, LoD and HiD, respectively, followed by downsampling:
Approximation — Convolve the rows and columns with a lowpass filter (
ll)Horizontal — Convolve the rows with a lowpass filter, and convolve the columns with a highpass filter (
lh)Vertical — Convolve the rows with a highpass filter, and convolve the columns with a lowpass filter (
hl)Diagonal — Convolve the rows and columns with a highpass filter (
hh)
The following chart describes the basic decomposition steps.

where
 — Downsample columns: keep the even-indexed columns
— Downsample columns: keep the even-indexed columns — Downsample rows: keep the even-indexed rows
— Downsample rows: keep the even-indexed rows — Convolve the rows of the entry with filter
X
— Convolve the rows of the entry with filter
X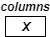 — Convolve the columns of the entry with filter
X
— Convolve the columns of the entry with filter
X
The decomposition is initialized by setting the approximation coefficients equal to the image s: cA0 = s.
References
[1] Daubechies, Ingrid. Ten Lectures on Wavelets. CBMS-NSF Regional Conference Series in Applied Mathematics 61. Philadelphia, Pa: Society for Industrial and Applied Mathematics, 1992.
[2] Mallat, S.G. “A Theory for Multiresolution Signal Decomposition: The Wavelet Representation.” IEEE Transactions on Pattern Analysis and Machine Intelligence 11, no. 7 (July 1989): 674–93. https://doi.org/10.1109/34.192463.
[3] Strang, Gilbert, and Truong Nguyen. Wavelets and Filter Banks. Rev. ed. Wellesley, Mass: Wellesley-Cambridge Press, 1997.
[4] Sweldens, Wim. “The Lifting Scheme: A Construction of Second Generation Wavelets.” SIAM Journal on Mathematical Analysis 29, no. 2 (March 1998): 511–46. https://doi.org/10.1137/S0036141095289051.
Extended Capabilities
Version History
Introduced in R2021bSee Also
ilwt2 | lwtcoef2 | haart2 | ihaart2 | liftingScheme