symaux
Symlet wavelet filter computation
Description
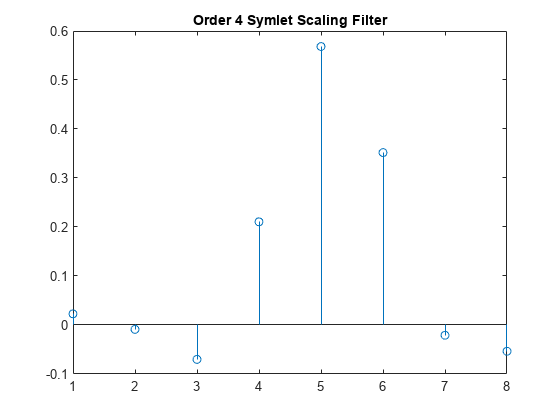
The symaux function generates the scaling filter coefficients
for the "least asymmetric" Daubechies wavelets.
w = symaux(n)n Symlet scaling filter such that sum(w) =
1.
Note
Instability may occur when
nis too large. Starting with values ofnin the 30s range, function output will no longer accurately represent scaling filter coefficients.As
nincreases, the time required to compute the filter coefficients rapidly grows.For
n= 1, 2, and 3, the ordernSymlet filters and ordernDaubechies filters are identical. See Extremal Phase Wavelet.
Examples
Input Arguments
Output Arguments
More About
References
[1] Daubechies, I. Ten Lectures on Wavelets, CBMS-NSF Regional Conference Series in Applied Mathematics. Philadelphia, PA: SIAM Ed, 1992.
[2] Oppenheim, Alan V., and Ronald W. Schafer. Discrete-Time Signal Processing. Englewood Cliffs, NJ: Prentice Hall, 1989.
Version History
Introduced before R2006a