wden
Automatic 1-D denoising
wden is no longer recommended. Use wdenoise
instead.
Syntax
Description
XD = wden(X,TPTR,SORH,SCAL,N,wname)XD of the signal X. The
function uses an N-level wavelet decomposition of
X using the specified orthogonal or biorthogonal wavelet
wname to obtain the wavelet coefficients. The thresholding selection
rule TPTR is applied to the wavelet decomposition.
SORH and SCAL define how the rule is
applied.
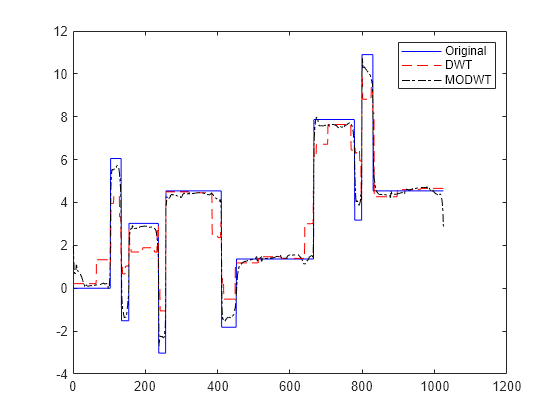
[
returns the number of coefficients by level for DWT denoising. See XD,CXD,LXD] = wden(___)wavedec for details. The LXD output is not supported for
MODWT denoising. The additional output arguments [CXD,LXD] are the
wavelet decomposition structure (see wavedec for more information) of the denoised signal
XD.
Examples
Input Arguments
Output Arguments
Algorithms
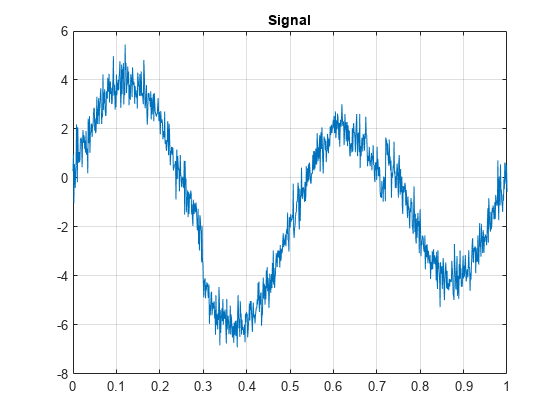
The most general model for the noisy signal has the following form:
where time n is equally spaced. In the simplest model, suppose that e(n) is a Gaussian white noise N(0,1), and the noise level σ is equal to 1. The denoising objective is to suppress the noise part of the signal s and to recover f.
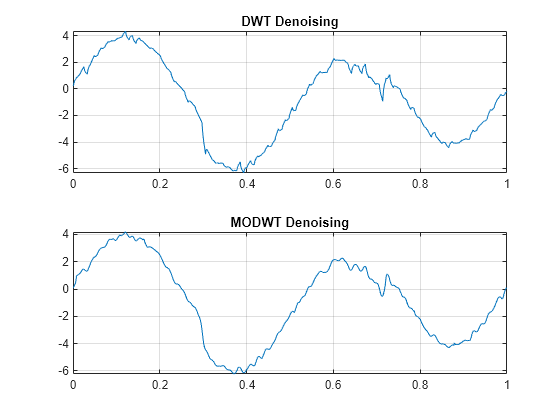
The denoising procedure has three steps:
Decomposition — Choose a wavelet, and choose a level
N. Compute the wavelet decomposition of the signal s at levelN.Detail coefficients thresholding — For each level from 1 to
N, select a threshold and apply soft thresholding to the detail coefficients.Reconstruction — Compute wavelet reconstruction based on the original approximation coefficients of level
Nand the modified detail coefficients of levels from 1 toN.
More details about threshold selection rules are in Wavelet Denoising and Nonparametric Function Estimation and in the help of the thselect function. Note that:
The detail coefficients vector is the superposition of the coefficients of f and the coefficients of e. The decomposition of e leads to detail coefficients that are standard Gaussian white noises.
Minimax and SURE threshold selection rules are more conservative and more convenient when small details of function f lie in the noise range. The two other rules remove the noise more efficiently. The option
'heursure'is a compromise.
In practice, the basic model cannot be used directly. To deal with model deviations, the
remaining parameter scal must be specified. It corresponds to threshold
rescaling methods.
The option
scal='one'corresponds to the basic model.The option
scal = 'sln'handles threshold rescaling using a single estimation of level noise based on the first-level coefficients.In general, you can ignore the noise level that must be estimated. The detail coefficients CD1 (the finest scale) are essentially noise coefficients with standard deviation equal to σ. The median absolute deviation of the coefficients is a robust estimate of σ. The use of a robust estimate is crucial. If level 1 coefficients contain f details, these details are concentrated in a few coefficients to avoid signal end effects, which are pure artifacts due to computations on the edges.
The option
scal='mln'handles threshold rescaling using a level-dependent estimation of the level noise.When you suspect a nonwhite noise e, thresholds must be rescaled by a level-dependent estimation of the level noise. The same kind of strategy is used by estimating σlev level by level. This estimation is implemented in the file
wnoisest, which handles the wavelet decomposition structure of the original signal s directly.
References
[1] Antoniadis, A., and G. Oppenheim, eds. Wavelets and Statistics, 103. Lecture Notes in Statistics. New York: Springer Verlag, 1995.
[2] Donoho, D. L. “Progress in Wavelet Analysis and WVD: A Ten Minute Tour.” Progress in Wavelet Analysis and Applications (Y. Meyer, and S. Roques, eds.). Gif-sur-Yvette: Editions Frontières, 1993.
[3] Donoho, D. L., and Johnstone, I. M. “Ideal Spatial Adaptation by Wavelet Shrinkage.” Biometrika, Vol. 81, pp. 425–455, 1994.
[4] Donoho, D. L. “De-noising by Soft-Thresholding.” IEEE Transactions on Information Theory, Vol. 42, Number 3, pp. 613–627, 1995.
[5] Donoho, D. L., I. M. Johnstone, G. Kerkyacharian, and D. Picard. “Wavelet Shrinkage: Asymptopia?” Journal of the Royal Statistical Society, series B. Vol. 57, Number 2, pp. 301–369, 1995.
Extended Capabilities
Version History
Introduced before R2006a