optimization-for-model-aircrafts

版本 1.0 (476.7 KB) 作者: MathWorks Student Competitions Team
This repository contains code that optimizes an aircraft with SAE Aero 2020 Regular Class problem statement as an example
0.0
(0)
85.0 次下载
更新时间 2022/8/11
在 GitHub 上查看许可证

Model Aircraft Design Optimization

Copyright 2022 The MathWorks® Inc.

View optimization-for-model-aircrafts on File Exchange

Introduction

This demo optimizes an aircraft with SAE Aero Design 2020 Regular Class problem statement as an example. A problem based approach is used to construct the design optimization problem. For SAE Aero Design 2020 Regular Class competition, each team's objective was to maximise their Final Flight Score (FFS) which was the sum of three highest Flight Scores (FS_i) and a Payload Prediction Bonus (PPB).

FFS = FS_1 + FS_2 + FS_3 + PPB

Each individual Flight Score (FS) was calculated as follows

FS = 120\times\frac{2\times N_s + W_{BP}}{b_w + l_{cargo}}

where,

N_s = No. of Spherical Payload

W_{BP} = Weight of Boxed Payload (lbs)

b_w = Wingspan (in)

l_{cargo} = Length of Payload Bay (in)

Therefore, this demo maximizes the following objective as it performs calculations in SI Units. Also, as only 1 spherical payload is considered.

Objective = 120\times \frac{2 + 2.2\times W_{BP}}{39.37\times(b_w + l_{cargo})}

A problem based approach is used to construct the design optimization problem. All expressions evaluated during problem setup are stored as a hierarchy of structure inside the aircraft structure. Four domain specific functions incrementally construct the design problem by modelling domain specific expressions and adding any relevant constraints. Finally, a 12 dimensional optimization problem is obtained with the following optimization variables.

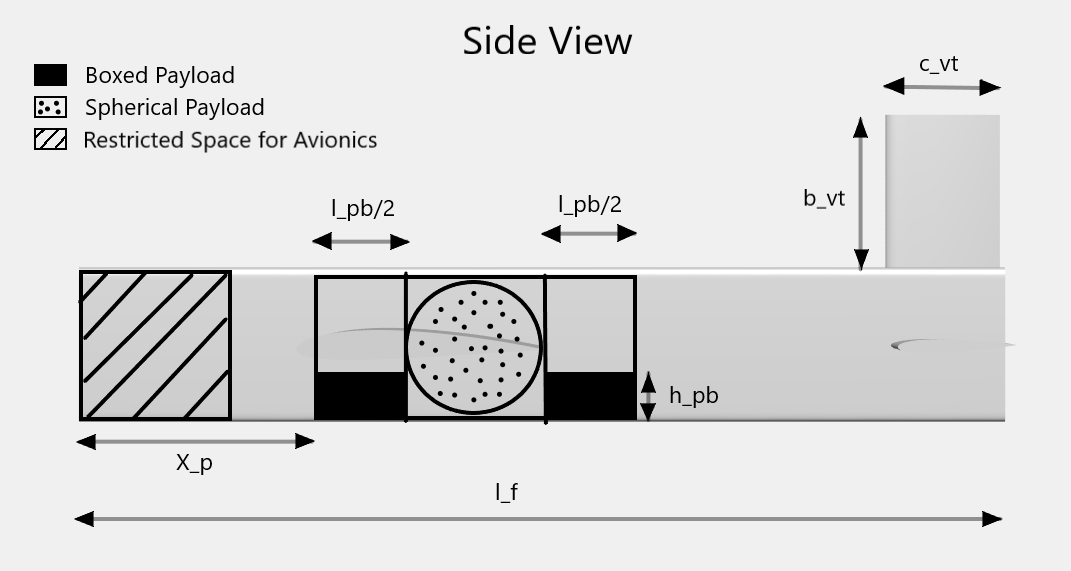
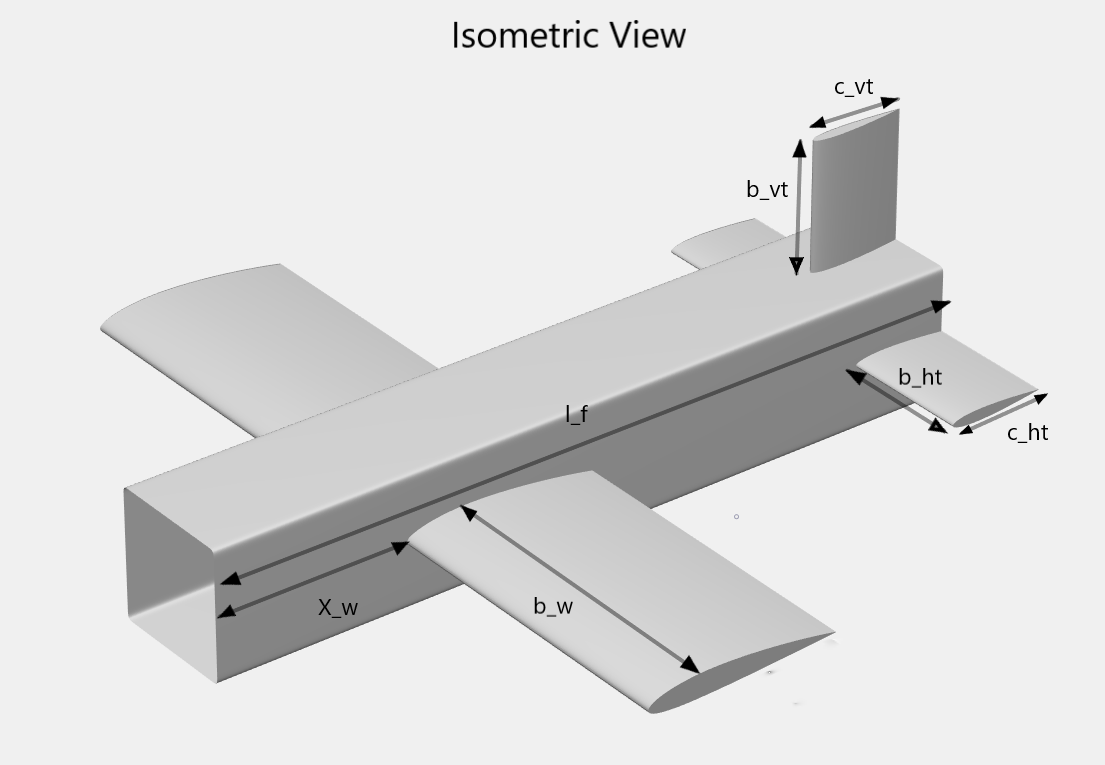
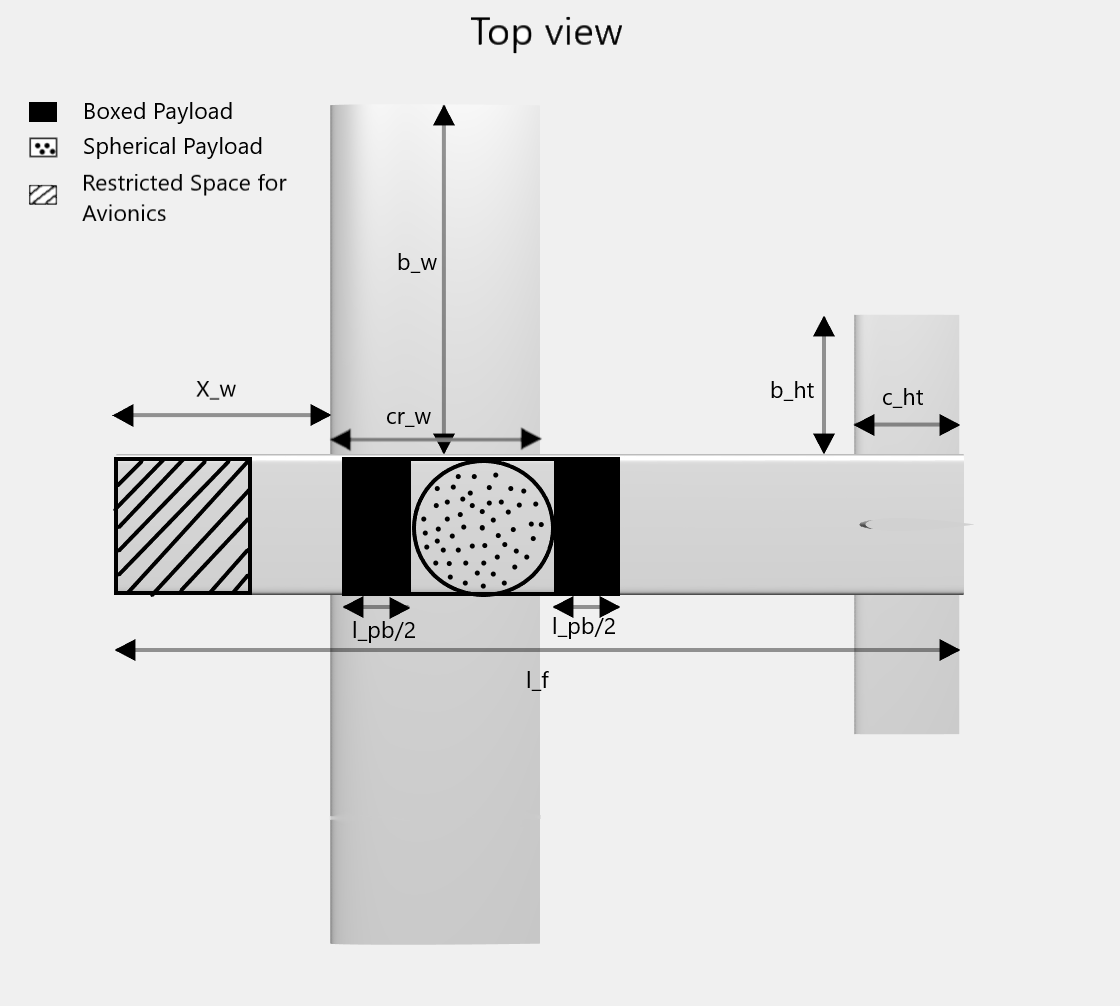
Symbolic Variable Physical Quantity
b_w Wing Half Span
cr_w Wing Root Chord
lambda_w Wing Taper Ratio
X_w Wing X Location
b_{ht} Horizontal Tail Half Span
c_{ht} Horizontal Tail Chord
b_{vt} Vertical Tail Half Span
c_{vt} Vertical Tail Chord
l_f Length of Fuselage
l_{pb} Length of Boxed Payload
h_{pb} Height of Boxed Payload
X_p Cargo Bay X Location

Following is the representation of optimization variables.

Drawing Drawing
Drawing

Code Structure

optimizeAircraft.mlx sets up and solves an aircraft design optimization problem. All other live functions model domain specific expressions and constraints and help incrementally setup the optimization problem.

Setup

  1. Clone the repository.
  2. Open MATLAB® and navigate to the repository.
  3. Open and execute the live script optimizeAircraft.mlx

MathWorks Products

Requires MATLAB release R2022a or newer

License

The license for Model Aircraft Design Optimization is available in the LICENSE.TXT file in this GitHub repository.

For any queries, contact the authors at roboticsarena@mathworks.com

引用格式

MathWorks Student Competitions Team (2024). optimization-for-model-aircrafts (https://github.com/mathworks/optimization-for-model-aircrafts/releases/tag/v1.0), GitHub. 检索时间: .

MATLAB 版本兼容性
创建方式 R2022a
兼容任何版本
平台兼容性
Windows macOS Linux

Community Treasure Hunt

Find the treasures in MATLAB Central and discover how the community can help you!

Start Hunting!

Aerodynamic Coefficients

Mass Moment of Inertia

版本 已发布 发行说明
1.0

要查看或报告此来自 GitHub 的附加功能中的问题，请访问其 GitHub 仓库。
要查看或报告此来自 GitHub 的附加功能中的问题，请访问其 GitHub 仓库。