asympPDC Package
by Koichi Sameshima and Luiz A. Baccalá
December 10, 2022
The asympPDC Package consists of MATLAB/Octave routines and functions collection for the analysis of multiple time series, such as EEG, biological signals and climate data, to infer directed interactions between structures in the frequency domain using Partial Directed Coherence (PDC) --- based on the concept of Granger causality --- and Directed Transfer Function (DTF), both in three metrics (Euclidean, diagonal and information) under the strict asymptotic statistics with p-values and confidence intervals also provided in the frequency domain.
We have included a Fast asymptotic PDC and DTF calculation algorithm, FastAsympAlg.m), recently made available by Rezaei et al. (2022) to which c struct variable output argument was added with fields that make it compatible with xplot.m PDC and DTF pretty plotting routine of the asympPDC Package. We have introduced some work-around to solve some syntax incompatibilities with older MATLAB versions and Octave as the original FastAsympAlg function seems to be implemented using the most recent version of MATLAB (after R2020a) syntax. The peformance of FastAsympAlg.m function is close to two-order of magnitude faster than original asympPDC Package routines. The performance speed gain is also dependent on the MATLAB release. We consider this is an important contribution that will allow users to apply PDC and DTF asymptotic statistics estimation in real-time connectivity problem when dealing with large number of channels, for instance 30 to 60 channels.
The asympPDC Package contains MATLAB/Octave m-files and subdirectories that you may download and copy into your local preferred working directory to execute them. To start, you should go to the package directory and run the startup.m script in the MATLAB/Octave command line window that will set paths and check for the requirements.
>> startupBesides adding the paths, startup.m will also check for the presence of the required MATLAB toolboxes (Control System
Toolbox(TM), Signal Processing Toolbox(TM), and Statistics Toolbox(TM) or Statistics or Machine Learning Toolbox(TM)) or Octave packages (control, signal, and statistics). This is a standalone package that will most likely work in the recent versions of Octave --- 6.3.0, 6.4.0 and 7.1.0. (Please report or suggest corrections to any issues related to compatibility with Octave).
To run all examples provided in ./examples subdirectory and verify if your installation is working properly, execute:
>> run_all_examplesIf "run_all_examples.m" completes successfully, congratulation, you should see 40+ overlapped figures that you could examine, in MATLAB, through
>> tilefigs1 or tilefigs2These commands tile the screen with figure windows. The tilefigs1 and tilefigs2 functions do not seem to work in the Octave environment.
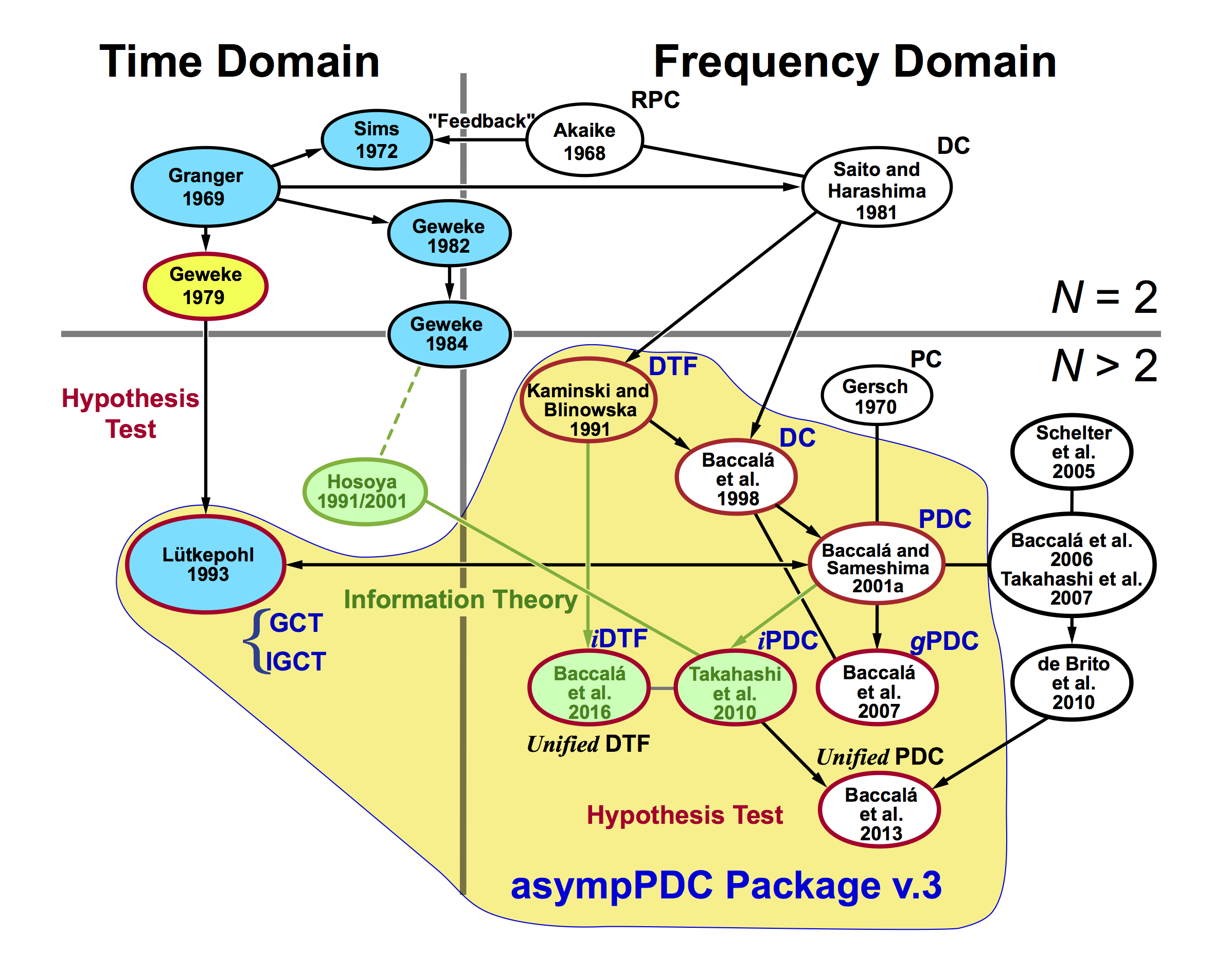
The figure bellow shows schematically the evolution path of directed connectivity, Granger causality and allied concepts developed along the last half-century from bivariate (N=2) to multivariate (N>2) time series, and from time domain to frequency domain analysis. The measures inside the yellow area are those implemented in the asympPDC Package.
-
Legend: N number of channels in time series; RPC - relative power contribution; DC - directed coherence or generalized directed transfer function; GCT - Granger causality test; iGCT - instantaneous Granger causality test; DTF - directed transfer function; PC - partial spectral coherence; PDC - partial directed coherence; gPDC - generalized partial directed coherence; iPDC - information partial directed coherence; iDTF - information directed transfer function.
-
Authors(sorted by year): Akaike 1968; Granger 1969; Gersch and Goddard 1970; Sims 1972; Geweke 1979; Saito and Harashima 1981; Geweke 1982; Geweke 1984; Kamiński and Blinowska 1991; Hosoya 1991; Lütkepohl 1993 --> 2005; Hosoya 1994; Baccalá et al. 1998; Baccalá and Sameshima 2001; Schelter et al. 2005; Baccalá et al. 2006; Takahashi et al. 2007; Baccalá et al. 2007; de Brito et al. 2010; Takahashi et al. 2010; Baccalá et al. 2013; Baccalá et al. 2016.
Lütkepohl, H. (1993) Introduction to Multiple Time Series Analysis. 2nd Edition, Springer, Berlin.
Saito, Y. and H. Harashima (1981) Tracking of information within multichannel record: causal analysis in EEG. In Recent Advances in EEG and EMG Data Processing. pp. 133--146, Amsterdam: Elsevier. (Hard to find !)
To get started, modify the analysis_template.m script file to adapt it to your needs and data sets. This template file
contains four examples of data that might be of help to deal with your
own data sets. The basic steps to set up and analyze a data set using the asympPDC Package are:
-
Import or open row-vectors data file;
-
Choose proper label for your data, assigning values to
chLabelsvariable; -
Data pre-processing: filtering, detrending and standardization (optional);
-
Multivariate autoregressive (MAR) model estimation, by choosing parameters, estimation algorithm and model order selection criterion;
-
PDC or DTF estimation, choosing analysis parameters such as significance levels for connectivity inference (
alpha,gct_signifandigct_signif) , metric for PDC/DTF, and number of frequency points, then callasymp_pdcorasymp_dtforFastAsympAlgfunction, and the analysis results will be saved in MATLABstructvariable that could be used for your further analysis, or to plot them; -
To visualize analysis results, use
xplot,xplot_pvaluesandxplot_titlefunctions to properly format and plot PDC/DTF and corresponding p-values results instruct variableobtained in the previous step in the frequency domain by choosingxplotandxplot_pvaluesplotting parameters, i.e.flgPrinting,w_max,flgColor,flgScale,flgMax, andflgSignifColor. See further details in thexplotfunction.
Examples from the literature are provided in ./examples directory with complete m-files with program structure similar to analysis_template.m.
We hope that the examples may help readers and users to understand
and/or gain further insight into Granger causality, instantaneous
Granger causality, PDC, and DTF concepts and the realm of connectivity
analysis. Use MATLAB/Octave help command to look up more
detail of each function or script. The help itself will also provide
links to the corresponding literature materials.
We hope you enjoy it. Good luck.
A. The asympPDC Package implementation is based mainly on the following articles and books
[1] L.A. Baccalá and K. Sameshima (2001). Partial directed coherence: a new concept in neural structure determination. Biol Cybern 84:463--474. https://doi.org/10.1007/PL00007990
[2] D.Y. Takahashi, L.A. Baccalá and K. Sameshima (2007), Connectivity inference between neural structures via partial directed coherence. J Appl Stat 34:1259--1273. https://doi.org/10.1080/02664760701593065
[3] L.A. Baccalá, C.S.N. De Brito, D.Y. Takahashi and K. Sameshima (2013). Unified asymptotic theory for all partial directed coherence forms. Philos T Roy Soc A 371:1--13. https://doi.org/10.1098/rsta.2012.0158
[4] M.J. Kamiński and K.J. Blinowska (1991). A new method of the description of the information flow in the brain structures. Biol Cybern 65:203--210. https://doi.org/10.1007/bf00198091
[5] L.A. Baccalá, D.Y. Takahashi and K. Sameshima (2016). Directed transfer function: unified asymptotic theory and some of its implications. IEEE T Bio-Med Eng 63:2450--2460. https://doi.org/10.1109/TBME.2016.2550199
[6] H. Lütkepohl (2005). New Introduction to Multiple Time Series Analysis. Springer-Verlag, Berlin.https://doi.org/10.1007/978-3-540-27752-1
[7] S.L. Marple Jr (1987). Digital Spectral Analysis with Application. Prentice-Hall, Englewood-Cliffs.
[8] T. Schneider and A. Neumaier (2001). Algorithm 808: ARfit - A Matlab package for the estimation of parameters and eigenmodes of multivariate autoregressive models. ACM Trans Math Softw 27:58-–65. https://doi.org/10.1145/382043.382316
[9] K. Sameshima and L.A. Baccalá Eds. (2014). Methods in Brain Connectivity Inference through Multivariate Time Series Analysis. CRC Press, Boca Raton. https://doi.org/10.1201/b16550
[10] L.A. Baccalá and K. Sameshima (2021). Partial directed coherence: twenty years on some history and an appraisal. Biol Cybern 115:195--204. https://doi.org/10.1007/s00422-021-00880-y
C. Things to come: Total PDC/DTF with asymptotic statistics, spectral factorization and faster PDC/DTF estimation algorithms . . .
[11] L.A. Baccalá and K. Sameshima (2021). Frequency domain repercussions of instantaneous Granger causality. Entropy 23(8):10.3390/e23081037 https://doi.org/10.3390/e23081037
[12] L.A. Baccalá and K. Sameshima (2022). Partial directed coherence and the vector autoregressive modelling myth and a caveat. Front Netw Physiol 2:845327. https://doi.org/10.3389/fnetp.2022.845327 (Note: MATLAB/Octave scripts and functions used to generate all four figures of this article are provided in ./demo/PDCVARMYTH2022 subdirectory. Follow the instructions in Readme file.)
[13] F. Rezaei, O. Alamoudi, S. Davani and S. Hou (2022) Fast asymptotic algorithm for real-time causal connectivity analysis of multivariate systems and signals. Signal Process 204:108822. https://doi.org/10.1016/j.sigpro.2022.108822 (Note: These authors optimized the asymp_pdc.m and asymp_dtf routines called FastAsympAlg.m basically by optimizing matrix operations and getting hid of sparse matrices that improved the speed by two order of magnitude. Look at compare_original_x_FastAsympAlg.m script in ./examples folder. )
These routines are distributed under GNU General Public License v3.0 under authorship of Koichi Sameshima and Luiz A. Baccalá - July 2022, December 2022
Koichi Sameshima and Luiz A. Baccalá (2022). asympPDC Package (Release v3.0.1 for File Exchange purpose · asymppdc/asympPDC · GitHub), GitHub. Retrieved August 12, 2022.