moving_average v3.1 (Mar 2008)
MOVING_AVERAGE(X,F) smooths the vector data X with a boxcar window of size 2F+1, i.e., by means of averaging each element with the F elements at his right and the F elements at his left. The extreme elements are also averaged but with less data, obviously. Leaving the edges intact. The method is really fast.
MOVING_AVERAGE2(X,M,N) smooths the matrix X with a boxcar window of size (2M+1)x(2N+1), i.e., by means of averaging each element with its surrounding elements that fits in the mentioned box centered on it. This one is also really fast. The elements at the edges are averaged too, but the corners are left intact.
NANMOVING_AVERAGE(X,F) or NANMOVING_AVERAGE(X,F,1) accept NaN's elements in the vector X; the latter interpolates also those NaN's elements surrounded by numeric elements.
NANMOVING_AVERAGE2(X,M,N) or NANMOVING_AVERAGE2(X,M,N,1) accept elements NaN's in the matrix X; the latter interpolates also those NaN elements surrounded by numeric elements.
[ New simple GAP filling ]:
SMOOTH_MAVERAGE(X,M,N,IND) this one smooths only the X(IND) elements. ignoring NaNs. This can be used to elimante GAPS on your data.
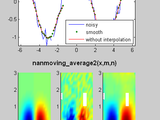
Each M-files has an example (see the screenshot).
Check below to see the CHANGES on v3.1.
Note: Looking the 2 dimensional code from MOVING_AVERAGE2.M (and RUNMEAN for some hints) somebody can easily make an N-dimensional MA. Would you?
引用格式
Carlos Adrian Vargas Aguilera (2024). moving_average v3.1 (Mar 2008) (https://www.mathworks.com/matlabcentral/fileexchange/12276-moving_average-v3-1-mar-2008), MATLAB Central File Exchange. 检索时间: .
MATLAB 版本兼容性
平台兼容性
Windows macOS Linux类别
- Signal Processing > Signal Processing Toolbox > Digital and Analog Filters > Digital Filter Analysis >
标签
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!moving_average_v3.1/
| 版本 | 已发布 | 发行说明 | |
|---|---|---|---|
| 1.0.0.0 | Use CUMSUM trick as Jos's RUNMEAN. Eliminates subfunctions. New screenshot.
|