Physical Constants

版本 1.2.2 (64.8 KB) 作者: Jorg Woehl

2022 CODATA recommended values of the fundamental constants in physics and chemistry

https://github.com/JorgWoehl/Constants

关注

5.0

(1)

166.0 次下载

更新时间 2024/5/13

在 GitHub 上查看许可证

Physical Constants

Constants for MATLAB provides easy access to the 2022 CODATA recommended values of nearly 150 fundamental constants from physics and chemistry, along with their uncertainties, units, names, and other metadata.

Constants has full symbolic math support and contains all historical CODATA datasets back to 1998.

Key Features and Benefits

Convenient: Simple dot notation with short, symbol-based variable names.
100% Accurate: Programmatically generated from the official CODATA source.
Rich Metadata: Access properties like uncertainty, units, names, and historical datasets back to 1998.
Symbolic Math Support: Perform arbitrary-precision calculations, unit conversions, and unit consistency checks using standard MATLAB functions.
Future-Proof: Designed to seamlessly accommodate future CODATA adjustments and higher-precision arithmetic in MATLAB.

Basic Usage

Load the latest (2022) values of physical constants:

const = Constants;

Tip

For easy access, save Constants.m to your userpath or add its parent folder to the MATLAB search path.

Access individual constants:

format long;
const.R   % Molar gas constant
% >> 8.314462618153240

const.NA  % Avogadro constant
% >> 6.02214076e+23

Constants have SI units unless the variable name ends in inUnit:

const.hbar             % Reduced Planck constant in SI units (J s)
% >> 1.054571817646156e-34

const.hbarineVseconds  % Reduced Planck constant in eV s
% >> 6.582119569509066e-16

Look up a constant:

const.find('charge')

Output:

    Variable                    Constant                     Unit
    ________    _________________________________________    ____
     ralpha     Alpha particle rms charge radius              m  
     rd         Deuteron rms charge radius                    m  
     e          Elementary charge (atomic unit of charge)     C  
     rp         Proton rms charge radius                      m

Get a list of available constants:

const.info

Output:

            Variable                                           Constant                                           Unit       
    ________________________    _______________________________________________________________________    __________________
    malpha                      Alpha particle mass                                                        kg                
    malphainu                   Alpha particle mass in u                                                   u                 
    Malpha                      Alpha particle molar mass                                                  kg mol^{-1}       
    ralpha                      Alpha particle rms charge radius                                           m                 
    angstromstar                Angstrom star                                                              m                 
    mu                          Atomic mass constant                                                       kg                
               :                                                   :                                               :         
    epsilonzero                 Vacuum electric permittivity                                               F m^{-1}          
    muzero                      Vacuum magnetic permeability                                               N A^{-2}          
    RK                          Von Klitzing constant                                                      ohm               
    sinsquaredthetaW            Weak mixing angle                                                          (unitless)        
    bprime                      Wien frequency displacement law constant                                   Hz K^{-1}         
    b                           Wien wavelength displacement law constant                                  m K               
	Display all 146 rows.

Advanced Usage

Properties and Metadata

Load all properties and metadata:

const = Constants('all');
const.me  % Properties and metadata for the electron mass

Output:

  struct with fields:

          id: 'electron mass (atomic unit of mass, natural unit of mass)'
        year: 2022
       value: 9.109383713900000e-31
       uncty: 2.800000000000000e-40
        unit: "kg"
        name: "electron mass (atomic unit of mass, natural unit of mass)"
     isExact: 0
       isIrr: 0
    symvalue: 0.00000000000000000000000000000091093837139
     symunit: [kg]
         sym: 0.00000000000000000000000000000091093837139*[kg]

Property	Description
`id`	Current name (and other names, if applicable)
`year`	Dataset year
`value`	Value
`uncty`	Uncertainty
`unit`	Unit
`name`	Name (and other names, if applicable) in dataset
`isExact`	`true` if the constant is exact
`isIrr`	`true` if the constant is irrational and exact
`symvalue`	Symbolic value (*)
`symunit`	Symbolic unit (*)
`sym`	Symbolic constant with unit (*)

(*) Requires a Symbolic Math Toolbox license.

Access individual properties:

const.me.value   % Value of the electron mass
% >> 9.1093837139e-31

const.me.uncty   % ... its associated uncertainty
% >> 2.8e-40

const.me.unit    % ... and units
% >> "kg"

Load individual properties:

uncty = Constants('uncty');
uncty.me         % Uncertainty in the value of the electron mass
% >> 2.8e-40

Note

The default is value. Calling Constants is equivalent to calling Constants('value').

Historical Data

Calling Constants with a second argument provides access to any of these datasets:

1998
2002
2006
2010
2014
2018
2022

Load values for a specific dataset:

const = Constants('value', '2006');
const.pg  % 2006 value of the proton g factor
% >> 5.585694713

Load values for the latest (2022) dataset:

const = Constants('value', 'latest');
const.Vm  % Current value of the molar volume of an ideal gas (273.15 K, 100 kPa)
% >> 0.022710954641486

Note

This is the default. Calling Constants(arg1) without a second argument is equivalent to calling Constants(arg1, 'latest').

Load values for all datasets (from oldest to most recent):

const = Constants('value', 'all');
const.h(1)    % 1998 value of the Planck constant
% >> 6.62606876e-34

const.h(4)    % 2010 value of the Planck constant
% >> 6.62606957e-34

const.h(end)  % Current (2022) value of the Planck constant
% >> 6.62607015e-34

Load all properties and metadata for all datasets:

const = Constants('all', 'all');
const.alpha   % Properties and metadata for the fine-structure constant (1998 to date)

Output:

  struct with fields:

          id: 'fine-structure constant'
        year: [1998 2002 2006 2010 2014 2018 2022]
       value: [0.007297352533000 0.007297352568000 0.007297352537600 0.007297352569800 0.007297352566400 … ] (1×7 double)
       uncty: [2.700000000000000e-11 2.400000000000000e-11 5.000000000000000e-12 2.400000000000000e-12 … ] (1×7 double)
        unit: [""    ""    ""    ""    ""    ""    ""]
        name: ["fine-structure constant"    "fine-structure constant"    "fine-structure constant"    …    ] (1×7 string)
     isExact: [0 0 0 0 0 0 0]
       isIrr: [0 0 0 0 0 0 0]
    symvalue: [1×7 sym]
     symunit: [1    1    1    1    1    1    1]
         sym: [1×7 sym]

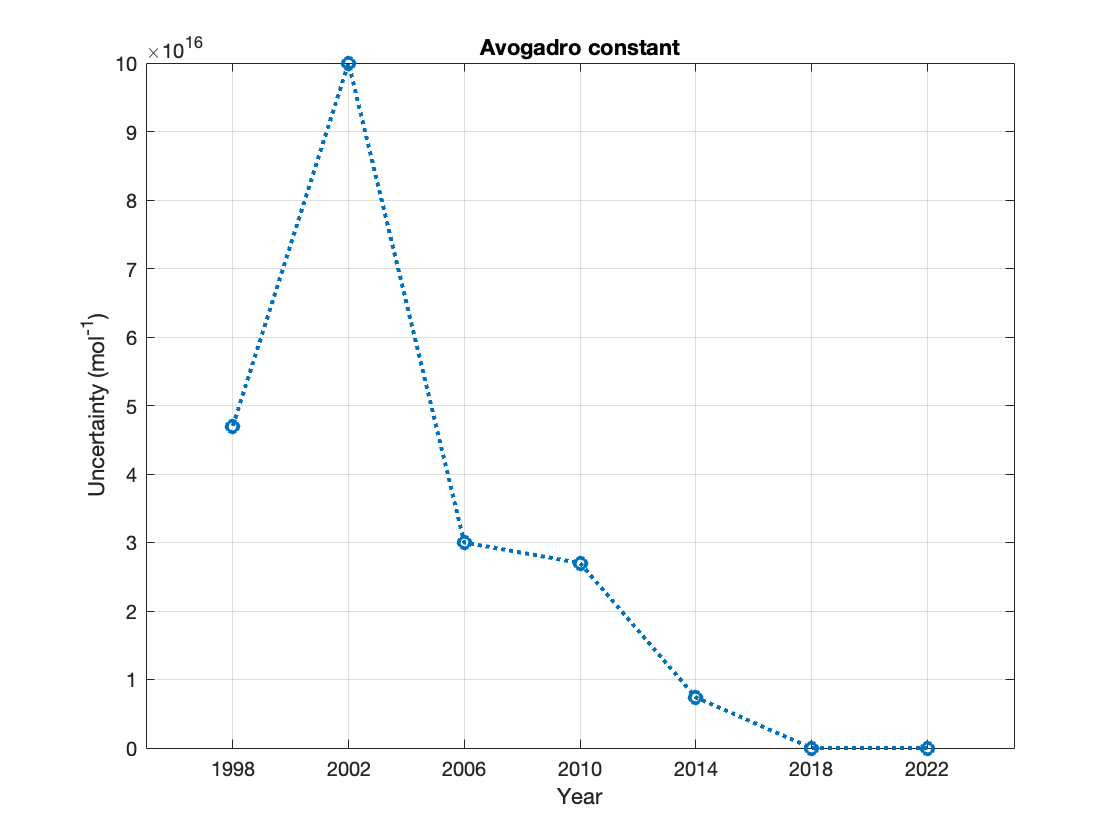
Example 1

const = Constants('all', 'all');
plot(const.NA.year, const.NA.uncty, ':o', 'LineWidth',2);
title(const.NA.id);
xlabel('Year');
ylabel("Uncertainty (" + const.NA.unit(end) + ")");
xticks(const.NA.year);
grid on;

The Avogadro constant was defined as an exact value (uncertainty: 0) when the SI Units were redefined in 2017.

Symbolic Math

Constants also provides symbolic representations of all values, units, and constants (values & units) to carry out symbolic manipulations and perform calculations with arbitrary accuracy.

`symvalue`: Symbolic Values

Exact constants, whose values are defined rather than experimentally determined, can be displayed with an arbitrary number of significant digits.

svalue = Constants('symvalue', '2018');
vpa(svalue.R, 150)     % 2018 value of the molar gas constant, rounded to 150 significant digits
vpa(svalue.hbar, 150)  % 2018 value of the reduced Planck constant, rounded to 150 significant digits

Output:

8.3144626181532399999999999999999999999986025942636401108474665474304748280360408924463157254169942689259187318384647369384765625
0.0000000000000000000000000000000001054571817646156391262428003302280744722889961594431207605200865210242417652521623612880705649658442982842269265184440305099090648037855420322457436

The first value, defined as R = N_A k in the 2018 dataset, is rational and has 128 significant digits. (Both the Avogadro constant N_A and the Boltzmann constant k are have exact, rational values in the dataset.)

The second value, defined as h / (2 π) in the 2018 dataset, is exact but irrational because pi is involved. (The Planck constant h has an exact, rational value in this dataset.)

Note

Even the 64-bit (double precision) floating-point values (value) of exact constants are computed from their definitions in Constants. This makes Constants future-proof should MATLAB ever be released with support for 128-bit (quadruple precision) or 256-bit (octuple precision) arithmetic.

`symunit`: Symbolic Units

Example 2

Verify units for the Rydberg constant, given by m_e e⁴ / (8 ε₀² h³ c) according to the Bohr model of the H atom:

sunit = Constants('symunit');
simplify(sunit.me * sunit.e^4 / (sunit.epsilonzero^2 * sunit.h^3 * sunit.c))
% >> 1/[m]

Caution

Choose your variable names wisely; sym and symunit are names of commands from the Symbolic Math Toolbox!

`sym`: Symbolic Constants

sconst = Constants('sym');
u = symunit;
speed = unitConvert(sconst.c, u.km/u.year)  % Speed of light in vacuum in km/year
% >> (47303652362904/5)*([km]/[year_Julian])

double(separateUnits(speed))                % Extract value and convert to double
% >> 9.460730472580801e+12

Example 3

According to Planck's blackbody radiation law, the proportionality constant between the total power flux and T⁴ is given by σ = 2 π⁵ k⁴ / (15 c² h³) :

sigma = sym('2')*sym(pi)^sym('5')*sconst.k^sym('4') / ...
	(sym('15')*sconst.c^sym('2')*sconst.h^sym('3'))
	
% Compare this with the (exact and irrational) Stefan-Boltzmann constant from 'Constants'
sconst.sigma

Output:

0.00000000018529443369510835899732062307541*pi^5*(([Hz]^3*[J]*[s]^2)/([K]^4*[m]^2))
0.00000000018529443369510835899732062307541*pi^5*([W]/([K]^4*[m]^2))

The values are obviously identical. Let's check if their units match as well:

checkUnits(sigma == sconst.sigma)

Output:

Consistent: 0
Compatible: 0

MATLAB thinks they are different, perhaps because sigma has messy units. Let's simplify it and try again:

sigma = simplify(sigma)

checkUnits(sigma == sconst.sigma)

Output:

0.000000056703744191844294539709967318892*(([Hz]*[kg])/([K]^4*[s]^2))

Consistent: 1
Compatible: 1

That's a match!

Background

Constants was built by scientists for scientists and engineers with a focus on ease of use, accuracy, and completeness.

The internationally recommended values of the basic constants and conversion factors of physics and chemistry are established by the Committee on Data of the International Science Council's (CODATA) Task Group on Fundamental Physical Constants. CODATA recommended values are adjusted in a four-year cycle and available on the National Institute of Standards and Technology (NIST) website. The 2022 CODATA recommended values were published on May 9, 2024 on the NIST website.

For each adjustment since 1998, NIST provides an ASCII file of all values. Constants.m is generated automatically by scraping the data from these ASCII files to avoid copy & paste errors and guarantee accuracy.

Frequently Asked Questions

A list of frequently asked questions is maintained separately from this README file.

List of Constants

Variable	Constant	Unit
`malpha`	Alpha particle mass	kg
`malphainu`	Alpha particle mass in u	u
`Malpha`	Alpha particle molar mass	kg mol^-1
`ralpha`	Alpha particle rms charge radius	m
`angstromstar`	Angstrom star	m
`mu`	Atomic mass constant	kg
`NA`	Avogadro constant	mol^-1
`muB`	Bohr magneton	J T^-1
`muBineVpertesla`	Bohr magneton in eV/T	eV T^-1
`azero`	Bohr radius (atomic unit of length)	m
`k`	Boltzmann constant	J K^-1
`kineVperkelvin`	Boltzmann constant in eV/K	eV K^-1
`Zzero`	Characteristic impedance of vacuum	ohm
`re`	Classical electron radius	m
`lambdaC`	Compton wavelength	m
`Gzero`	Conductance quantum	S
`KJninety`	Conventional value of Josephson constant	Hz V^-1
`Aninety`	Conventional value of ampere-90	A
`Cninety`	Conventional value of coulomb-90	C
`Fninety`	Conventional value of farad-90	F
`Hninety`	Conventional value of henry-90	H
`Omeganinety`	Conventional value of ohm-90	ohm
`Vninety`	Conventional value of volt-90	V
`RKninety`	Conventional value of von Klitzing constant	ohm
`Wninety`	Conventional value of watt-90	W
`xuCu`	Copper x unit	m
`gd`	Deuteron g factor	(unitless)
`mud`	Deuteron magnetic moment	J T^-1
`md`	Deuteron mass	kg
`mdinu`	Deuteron mass in u	u
`Md`	Deuteron molar mass	kg mol^-1
`rd`	Deuteron rms charge radius	m
`ge`	Electron g factor	(unitless)
`gammae`	Electron gyromagnetic ratio	s^-1 T^-1
`gammaeinMHzpertesla`	Electron gyromagnetic ratio in MHz/T	MHz T^-1
`mue`	Electron magnetic moment	J T^-1
`ae`	Electron magnetic moment anomaly	(unitless)
`me`	Electron mass (atomic unit of mass, natural unit of mass)	kg
`meinu`	Electron mass in u	u
`Me`	Electron molar mass	kg mol^-1
`eV`	Electron volt	J
`eVinhartree`	Electron volt-hartree relationship	E_h
`e`	Elementary charge (atomic unit of charge)	C
`F`	Faraday constant	C mol^-1
`alpha`	Fine-structure constant	(unitless)
`cone`	First radiation constant	W m^2
`coneL`	First radiation constant for spectral radiance	W m^2 sr^-1
`Eh`	Hartree energy (atomic unit of energy)	J
`EhineV`	Hartree energy in eV	eV
`gh`	Helion g factor	(unitless)
`muh`	Helion magnetic moment	J T^-1
`mh`	Helion mass	kg
`mhinu`	Helion mass in u	u
`Mh`	Helion molar mass	kg mol^-1
`sigmah`	Helion shielding shift	(unitless)
`DeltanuCs`	Hyperfine transition frequency of Cs-133	Hz
`KJ`	Josephson constant	Hz V^-1
`jouleineV`	Joule-electron volt relationship	eV
`jouleinhartree`	Joule-hartree relationship	E_h
`kginu`	Kilogram-atomic mass unit relationship	u
`a`	Lattice parameter of silicon	m
`dtwotwozero`	Lattice spacing of ideal Si (220)	m
`nzero`	Loschmidt constant (273.15 K, 100 kPa)	m^-3
`nzeroSTPold`	Loschmidt constant (273.15 K, 101.325 kPa)	m^-3
`Kcd`	Luminous efficacy	lm W^-1
`Phizero`	Magnetic flux quantum	Wb
`R`	Molar gas constant	J mol^-1 K^-1
`Mu`	Molar mass constant	kg mol^-1
`MtwelveC`	Molar mass of carbon-12	kg mol^-1
`Vm`	Molar volume of ideal gas (273.15 K, 100 kPa)	m^3 mol^-1
`VmSTPold`	Molar volume of ideal gas (273.15 K, 101.325 kPa)	m^3 mol^-1
`VmSi`	Molar volume of silicon	m^3 mol^-1
`xuMo`	Molybdenum x unit	m
`lambdaCmu`	Muon Compton wavelength	m
`gmu`	Muon g factor	(unitless)
`mumu`	Muon magnetic moment	J T^-1
`amu`	Muon magnetic moment anomaly	(unitless)
`mmu`	Muon mass	kg
`mmuinu`	Muon mass in u	u
`Mmu`	Muon molar mass	kg mol^-1
`lambdaCn`	Neutron Compton wavelength	m
`gn`	Neutron g factor	(unitless)
`gamman`	Neutron gyromagnetic ratio	s^-1 T^-1
`gammaninMHzpertesla`	Neutron gyromagnetic ratio in MHz/T	MHz T^-1
`mun`	Neutron magnetic moment	J T^-1
`mn`	Neutron mass	kg
`mninu`	Neutron mass in u	u
`Mn`	Neutron molar mass	kg mol^-1
`G`	Newtonian constant of gravitation	m^3 kg^-1 s^-2
`muN`	Nuclear magneton	J T^-1
`muNineVpertesla`	Nuclear magneton in eV/T	eV T^-1
`h`	Planck constant	J Hz^-1
`hineVseconds`	Planck constant in eV/Hz	eV Hz^-1
`lP`	Planck length	m
`mP`	Planck mass	kg
`TP`	Planck temperature	K
`tP`	Planck time	s
`lambdaCp`	Proton Compton wavelength	m
`gp`	Proton g factor	(unitless)
`gammap`	Proton gyromagnetic ratio	s^-1 T^-1
`gammapinMHzpertesla`	Proton gyromagnetic ratio in MHz/T	MHz T^-1
`mup`	Proton magnetic moment	J T^-1
`sigmapprime`	Proton magnetic shielding correction	(unitless)
`mp`	Proton mass	kg
`mpinu`	Proton mass in u	u
`Mp`	Proton molar mass	kg mol^-1
`rp`	Proton rms charge radius	m
`lambdabarC`	Reduced Compton wavelength (natural unit of length)	m
`hbar`	Reduced Planck constant (atomic unit of action, natural unit of action)	J s
`hbarineVseconds`	Reduced Planck constant in eV s (natural unit of action in eV s)	eV s
`lambdabarCmu`	Reduced muon Compton wavelength	m
`lambdabarCn`	Reduced neutron Compton wavelength	m
`lambdabarCp`	Reduced proton Compton wavelength	m
`lambdabarCtau`	Reduced tau Compton wavelength	m
`Rinfinity`	Rydberg constant	m^-1
`ctwo`	Second radiation constant	m K
`gammahprime`	Shielded helion gyromagnetic ratio	s^-1 T^-1
`gammahprimeinMHzpertesla`	Shielded helion gyromagnetic ratio in MHz/T	MHz T^-1
`muhprime`	Shielded helion magnetic moment	J T^-1
`gammapprime`	Shielded proton gyromagnetic ratio	s^-1 T^-1
`gammapprimeinMHzpertesla`	Shielded proton gyromagnetic ratio in MHz/T	MHz T^-1
`mupprime`	Shielded proton magnetic moment	J T^-1
`sigmadp`	Shielding difference of d and p in HD	(unitless)
`sigmatp`	Shielding difference of t and p in HT	(unitless)
`c`	Speed of light in vacuum (natural unit of velocity)	m s^-1
`gzero`	Standard acceleration of gravity	m s^-2
`atm`	Standard atmosphere	Pa
`ssp`	Standard-state pressure	Pa
`sigma`	Stefan-Boltzmann constant	W m^-2 K^-4
`lambdaCtau`	Tau Compton wavelength	m
`mtau`	Tau mass	kg
`mtauinu`	Tau mass in u	u
`Mtau`	Tau molar mass	kg mol^-1
`sigmae`	Thomson cross section	m^2
`gt`	Triton g factor	(unitless)
`mut`	Triton magnetic moment	J T^-1
`mt`	Triton mass	kg
`mtinu`	Triton mass in u	u
`Mt`	Triton molar mass	kg mol^-1
`u`	Unified atomic mass unit	kg
`epsilonzero`	Vacuum electric permittivity	F m^-1
`muzero`	Vacuum magnetic permeability	N A^-2
`RK`	Von Klitzing constant	ohm
`sinsquaredthetaW`	Weak mixing angle	(unitless)
`bprime`	Wien frequency displacement law constant	Hz K^-1
`b`	Wien wavelength displacement law constant	m K

引用格式

Jorg Woehl (2024). Physical Constants (https://github.com/JorgWoehl/Constants/releases/tag/v1.2.2), GitHub. 检索时间: 2024/11/22.

MATLAB 版本兼容性

创建方式 R2023b

与 R2023b 及更高版本兼容

平台兼容性

Windows macOS Linux

标签添加标签

Community Treasure Hunt

Find the treasures in MATLAB Central and discover how the community can help you!

Start Hunting!

Constants

版本	已发布	发行说明
1.2.2	2024/5/13	See release notes for this release on GitHub: https://github.com/JorgWoehl/Constants/releases/tag/v1.2.2	下载
1.2.1	2024/5/13	See release notes for this release on GitHub: https://github.com/JorgWoehl/Constants/releases/tag/v1.2.1	下载
1.2	2024/5/12	See release notes for this release on GitHub: https://github.com/JorgWoehl/Constants/releases/tag/v1.2	下载
1.1.2	2024/3/25	See release notes for this release on GitHub: https://github.com/JorgWoehl/Constants/releases/tag/1.1.2	下载
1.1.1	2024/3/25	See release notes for this release on GitHub: https://github.com/JorgWoehl/Constants/releases/tag/v1.1.1	下载
1.1.0	2024/3/25	See release notes for this release on GitHub: https://github.com/JorgWoehl/Constants/releases/tag/v1.1.0	下载
1.0.0	2024/3/24		下载

要查看或报告此来自 GitHub 的附加功能中的问题，请访问其 GitHub 仓库。

Physical Constants

Physical Constants

Key Features and Benefits

Basic Usage

Advanced Usage

Properties and Metadata

Historical Data

Example 1

Symbolic Math

symvalue: Symbolic Values

symunit: Symbolic Units

Example 2

sym: Symbolic Constants

Example 3

Background

Frequently Asked Questions

List of Constants

引用格式

MATLAB 版本兼容性

平台兼容性

标签 添加标签

Community Treasure Hunt

探索实时编辑器

`symvalue`: Symbolic Values

`symunit`: Symbolic Units

`sym`: Symbolic Constants

标签添加标签