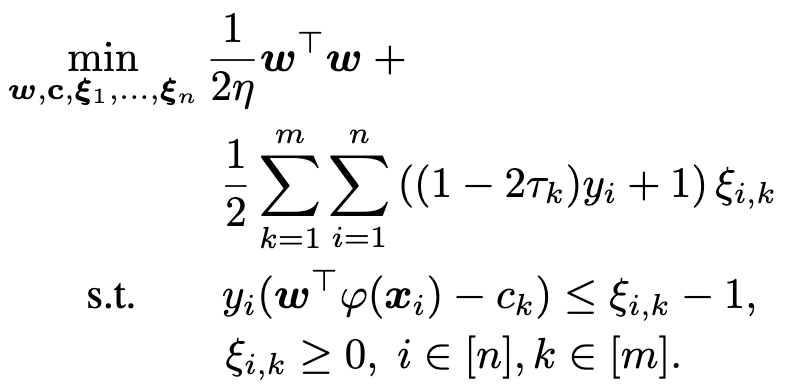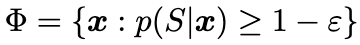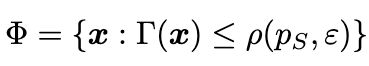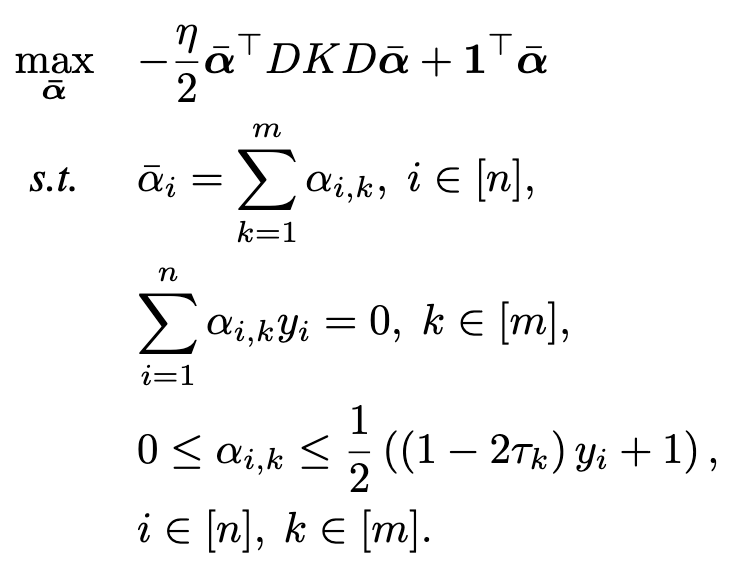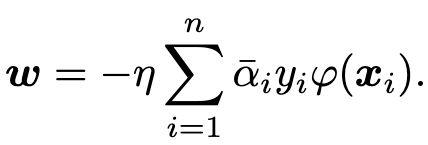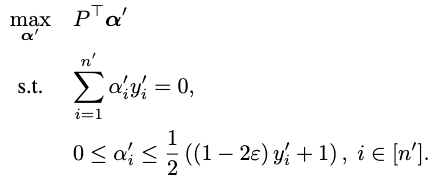Multi Cost SVM (MC-SVM) is a variant of Support Vector Machines (SVM) designed to accommodate multiple cost scenarios. By introducing multiple weighting parameters <math-renderer class="js-inline-math" style="display: inline" data-static-url="https://github.githubassets.com/static" data-run-id="5d26f3cd5177cee34992c9bdd39339ab">$\tau$</math-renderer>, MC-SVM adapts the cost function to balance false positive and false negative errors, enhancing the model's robustness across diverse scenarios. The result is a separation hyperplane indipendent from the sample probability of the data.

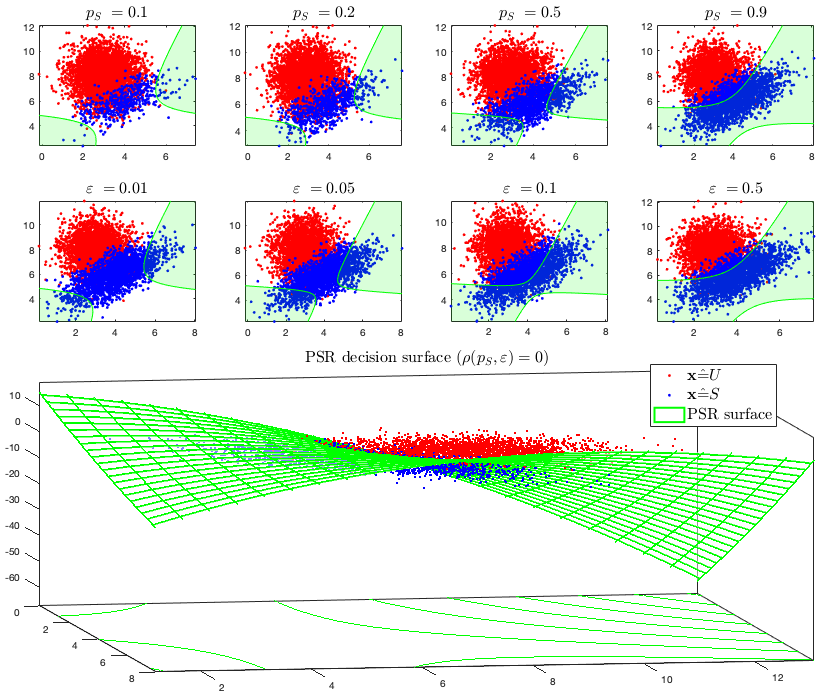
This algorithm was inspired by the concept of Probabilistic Safety Region (PSR)

i.e., the region where in high probability is possible to observe the event <math-renderer class="js-inline-math" style="display: inline" data-static-url="https://github.githubassets.com/static" data-run-id="5d26f3cd5177cee34992c9bdd39339ab">$S$</math-renderer>, that, we can suppose, represents a "safe" situation. It is interesting to note, and these considerations are reported in the code, that for exponential distributions the PSR takes the interesting form of a radius controllable set:

Parameterized Cost Function: MC-SVM incorporates a parameter <math-renderer class="js-inline-math" style="display: inline" data-static-url="https://github.githubassets.com/static" data-run-id="5d26f3cd5177cee34992c9bdd39339ab">$\tau$</math-renderer> to influence the cost function's behavior towards different types of errors. This parameterization allows to weight the SVMs with different weighting parameters, reducing the unbalanceness of the data and helping training a more robust algorithm.

System of SVMs: The algorithm constructs a system of <math-renderer class="js-inline-math" style="display: inline" data-static-url="https://github.githubassets.com/static" data-run-id="5d26f3cd5177cee34992c9bdd39339ab">$m$</math-renderer> SVMs using the same dataset but varying weights and offsets. Each SVM corresponds to a different value of <math-renderer class="js-inline-math" style="display: inline" data-static-url="https://github.githubassets.com/static" data-run-id="5d26f3cd5177cee34992c9bdd39339ab">$\tau$</math-renderer>, enabling the model to adapt to various cost scenarios.

The optimization problem is solved in its dual form

leading to the separation hyperplane

The error in the prediction (false or negative ratio) is then controlled using the following algorithm, based on the quantile regression idea that, discarding the regularization parameter (possible because we computed an independent hyperplane with the algorithm above), the weighting parameter corresponds to the false negative ratio:

To utilize MC-SVM in your projects, follow these steps:

Download the Code: Clone the repository containing the MC-SVM implementation.

Configure Parameters: Adjust the value of <math-renderer class="js-inline-math" style="display: inline" data-static-url="https://github.githubassets.com/static" data-run-id="5d26f3cd5177cee34992c9bdd39339ab">$\tau$</math-renderer>, the kernels and other parameters according to your application requirements.

Train the Model: Provide your dataset and train the MC-SVM model using the provided training algorithm.

Evaluate Performance: Evaluate the model's performance on your test dataset and analyze its behavior under different cost scenarios.

Matlab

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

For a dataset composed by data sampled with different probabilities

Tau = rand(1,9); m = size(Tau,2);

kernel = 'polynomial';

param = 3;

eta = .001;

alpha_bar = MCSVM_Train(Xtr, Ytr, kernel, param, Tau, eta); # best hyperplane common to all the data

Specializing to a dataset with a known (or estimated) sample probability

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

tau = 1-epsilon; # to control the false positives

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

alpha_c = SSVM_Train_c(Xtr, Ytr, Xcl_p, Ycl_p, kernel, param, tau, eta, alpha_bar);

b = offset_c(Xtr, Ytr, Xcl_p, Ycl_p, alpha_c, kernel, param, eta, tau, alpha_bar); # best offset that realizes the control of the false positive ration on the desired (calibration) set.

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

test

y_pred_ts = SSVM_Test(Xtr, Ytr, Xts_p, alpha_bar, b, 0, kernel, param, eta);

[TPR_SSVM, FPR_SSVM, TNR_SSVM, FNR_SSVM, F1_SSVM, ACC_SSVM] = ConfusionMatrix(Yts_p, y_pred_ts,'on');

disp(['False positive rate:',num2str(FPR_SSVM)])

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

Contributions to the MC-SVM algorithm are welcome! Feel free to submit bug reports, feature requests, or pull requests to improve the algorithm's functionality and usability.