fit_ellipse

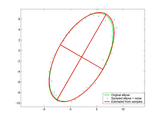
This function uses the Least-Squares criterion for estimation of the best fit to an ellipse from a given set of points (x,y). The LS estimation is done for the conic representation of an ellipse (with a possible tilt).

Conic Ellipse representation = a*x^2+b*x*y+c*y^2+d*x+e*y+f=0
(Tilt/orientation for the ellipse occurs when the term x*y exists (i.e. b ~= 0))

Later, after the estimation, the tilt is removed from the ellipse (using a rotation matrix) and then, the rest of the parameters which describes an ellipse are extracted from the conic representation.

For debug purposes, the estimation can be drawn on top of a given axis handle.

Note:
1) This function does not work on a three-dimensional axis system. (only 2D)
2) At least 5 points are needed in order to estimate the 5 parameters of the ellipse.
3) If the data is a hyperbola or parabula, the function return empty fields and a status indication